
- •Основные положения
- •1. Содержание расчетно-пояснительной записки и ее оформление
- •1.1. Общие требования
- •1.2. Задание к курсовой работе
- •Для полученной расчетной схемы выполнить:
- •2 Методические указания
- •2.1.Трехфазные цепи
- •2.2 Матричные методы расчета линейных цепей
- •2.1. Обобщённое и аналитическое представления схем
- •2.2. Основные матричные уравнения электрических цепей
- •2.3. Метод симметричных составляющих
- •2.3.1. Симметричные составляющие трехфазной системы величин
- •2.3.2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- •2.4 Фильтры симметричных составляющих
- •2.4.1 Фильтры напряжения нулевой последовательности (фннп)
- •2.4.2 Фильтры тока нулевой последовательности (фтнп)
- •4.3 Фильтр напряжения обратной последовательности (фноп)
- •4.4 Фильтры тока обратной последовательности (фтоп)
- •2.5. Анализ цепей с несинусоидальными периодическими источниками
- •2.5.1 Общие положения
- •2.5.2 Особенности работы трехфазных систем, вызываемые гармониками, кратными трем.
- •2.6.Анализ переходных процессов в линейных цепях
- •2.6.1 Возникновение переходных процессов. Понятие о коммутации
- •2.6.2 Законы коммутации
- •2.6.3 Классический метод расчета переходного процесса.
- •2.6.4 Операторный метод
- •2.6.5 Метод переменных состояния
- •2.6.5.1 . Общие понятия и определения
- •2.6.5.2 Формирование уравнения в матричной форме по методу наложения
- •2.6.6 Расчёт переходного процесса с помощью интеграла Дюамеля
- •3. Пример выполнения курсовой работы
- •3.1Постановка задачи в курсовой работы
- •Пример выполнения задачи № 1
- •Пример выполнения задачи № 1 в программеMathCad
- •Пример моделирование задачи № 1 в программе matlab и simulink
- •3.3 Пример выполнения задачи №2.
- •Пример выполнения задачи № 2 в программеMathCad
- •Пример моделирование задачи № 2 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №3
- •Пример выполнения задачи № 3 в программеMathCad
- •Пример моделирование задачи № 3 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №4.
- •Пример выполнения задачи № 4 в программеMathCad
- •Пример моделирование задачи № 4 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №5.
- •Пример выполнения задачи № 5 в программеMathCad
- •Пример моделирование задачи № 5 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №6
- •Пример выполнения задачи № 6 в программеMathCad
- •Пример моделирование задачи № 6 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №7
- •Пример выполнения задачи № 7 в программеMathCad
- •Пример моделирование задачи № 7 в программеMatlab и simulink
- •3.4 Пример выполнения задачи №8
- •1 Рассчитать переходной процесс для ток iA(t), в полученной однофазной классическим методом
- •3.3 Пример выполнения задачи №9
- •Пример моделирование задачи № 9 в программеMatlab и simulink
- •Пример моделирование задачи № 9 в программеMatlab и simulink
- •Библиографический список
- •Рассоха Дмитрий Павлович
2.5.2 Особенности работы трехфазных систем, вызываемые гармониками, кратными трем.
Электродвижущие силы каждой фазы трехфазного трансформатора или трехфазного генератора часто оказываются несинусоидальными. Каждая ЭДС повторяет по форме остальные со сдвигом на одну треть периода (Т/3) и может быть разложена на гармоники. Постоянная составляющая обычно отсутствует.
Пусть
k-гармоника
ЭДС фазы A
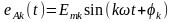 .
.
Так как ЭДС фазы В отстает от ЭДС фазы А на T/3 периода, а ЭДС фазы С опережает ЭДС фазы А на Т/3, то k-гармоники ЭДС в фазе В и в фазе С соответственно:
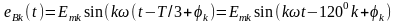 ;
;
 ;
;
 .
.
Если k =1, 4, 7, 10, то k-гармоника ЭДС фазы В отстает на 1209 от гармоники ЭДС фазы А. Следовательно, 1, 4, 7, 10-я гармоники образуют систему прямой последовательности фаз.
Если k =2, 5, 8, 11, то k-гармоника ЭДС фазы В опережает k-гармонику фазы A на 120°. Следовательно, 2, 5, 8-я и т. д. гармоники образуют системы обратной последовательности.
Гармоники,
кратные трем (k
=3,
6, 9), образуют
систему нулевой п оследовательности,
т. е. третьи гармоники ЭДС - во всех трех
фазах совпадают по фазе (3120°=
360°):
оследовательности,
т. е. третьи гармоники ЭДС - во всех трех
фазах совпадают по фазе (3120°=
360°):
 .
.
Шестые гармоники ЭДС также совпадают по фазе и т. д.
Совпадение по фазе третьих гармоник ЭДС во всех трех фазах проиллюстрируем графически.
На
рис. 5.2 ЭДС
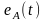 ,
,

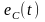 представляют собой три фазные ЭДС
трехфазного генератора. Они имеют
прямоугольную форму и сдвинуты по
отношению друг к другу на одну треть
периода основной частоты.
представляют собой три фазные ЭДС
трехфазного генератора. Они имеют
прямоугольную форму и сдвинуты по
отношению друг к другу на одну треть
периода основной частоты.
На том же рисунке показаны первая и третья гармоники каждой ЭДС. Из рисунка видно, что третьи гармоники ЭДС действительно находятся в фазе.
Рассмотрим особенности работы трехфазных систем, вызываемые гармониками, кратными трем.
П
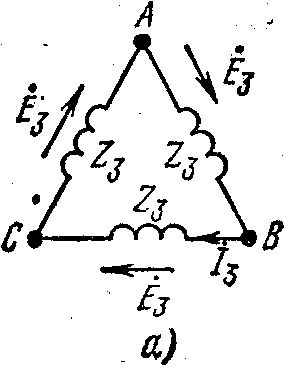
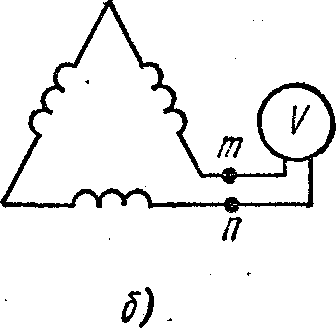
Рис. 5.3
ри соединении обмоток трехфазного генератора (трехфазного трансформатора) в треугольник (рис. 5.3, а) по ним протекают токи гармоник, кратных трем, даже при отсутствии внешней нагрузки.Алгебраическая сумма третьих гармоник ЭДС в треугольнике равна 3E3.
Но алгебраическая сумма первых гармоник ЭДС и всех гармоник ЭДС, не кратных трем, равна нулю, поэтому от перечисленных гармоник при отсутствии нагрузки по замкнутому треугольнику ток протекать не будет.
Обозначим
сопротивление обмотки каждой фазы для
третьей гармоники Z3,
тогда ток третьей гармоники в треугольнике
 ,
аналогично, ток шестой гармоники
,
аналогично, ток шестой гармоники
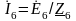
где E6 – действующее значение шестой гармоники фазной ЭДС;
Z6 –сопротивление фазы для шестой гармоники. Действующее значение тока, протекающего по замкнутому треугольнику в схеме рис. 5.3, а.
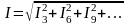 .
.
2. Если соединить обмотки трехфазного генератора (трехфазного трансформатора) в открытый треугольник (рис. 5.3, б), то при наличии в фазных ЭДС гармоник, кратных трем, на зажимах т и п будет напряжение, равное сумме ЭДС гармоник, кратных трем:
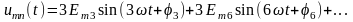 .
.
Показание
вольтметра в схеме рис. 5.3, б:
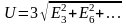 .
.
3. В линейном напряжении независимо от того, в звезду или треугольник соединены обмотки генератора (трансформатора), кратные трем гармоники отсутствуют, если нагрузка равномерна.
Рассмотрим
сначала схему соединения трехфазного
источника ЭДС в треугольник (рис. 5.3, а),
при отсутствии внешней нагрузки.
Обозначив
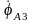 –
потенциал точки A
и
–
потенциал точки A
и
 – потенциал точки В
по третьей гармонике, получим
– потенциал точки В
по третьей гармонике, получим
.
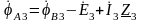
Н о
о
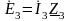 следовательно,
следовательно,
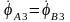 .
При наличии равномерной нагрузки,
соединенной в треугольник, каждая фаза
генератора (трансформатора) и параллельно
ей присоединенная нагрузка могут быть
заменены, эквивалентной ветвью с
некоторой ЭДС
.
При наличии равномерной нагрузки,
соединенной в треугольник, каждая фаза
генератора (трансформатора) и параллельно
ей присоединенная нагрузка могут быть
заменены, эквивалентной ветвью с
некоторой ЭДС
 и сопротивлением
и сопротивлением
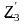 .
На полученную схему можно распространить
вывод, сделанный для случая отсутствия
внешней нагрузки.
.
На полученную схему можно распространить
вывод, сделанный для случая отсутствия
внешней нагрузки.
При соединении в звезду трехфазного источника ЭДС (рис. 5.4) линейное напряжение третьей гармоники равно разности соответствующих фазовых напряжений. Так как третьи гармоники в фазовых напряжениях совпадают по фазе, то при составлении этой разности они вычитаются.
В фазовом напряжении могут присутствовать все гармоники (постоянная составляющая обычно отсутствует). Следовательно, действующее значение фазового напряжения
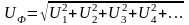 .
.
В линейном напряжении схемы рис. 5.3 отсутствуют гармоники, кратные трем; поэтому
 .
.
Отношение
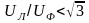 если есть гармоники, кратные трем.
если есть гармоники, кратные трем.
4.
При соединении генератора и равномерной
нагрузки в звезду и отсутствии нулевого
провода токи третьих и других гармоник
нулевой последовательности не могут
протекать по линейным проводам. Поэтому
между нулевыми точками приемника 0’
и генератора 0
(при Z0=)
действует напряжение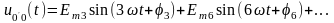 , действующее значение которого
, действующее значение которого
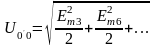 .
.
5.
Если в схеме звезда–звезда при равномерной
нагрузке фаз сопротивление нагрузки
для третьей гармоники обозначить
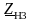 ,
а сопротивление нулевого провода для
третьей гармоники –
,
а сопротивление нулевого провода для
третьей гармоники – ,
то по нулевому проводу будет протекать
ток третьей гармоники
,
то по нулевому проводу будет протекать
ток третьей гармоники

Эта
формула получена путем составления
уравнения по второму закону Кирхгофа
для контура, образованного какой-либо
фазой и нулевым проводом. По
каждому из линейных проводов будет
протекать ток третьей гармоники
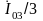
Аналогично находят токи и других гармоник, кратных трем.
