7.3. Меры сходства групп объектов (классов)
Другой
важной величиной в кластерном анализе
является расстояние между целыми
группами объектов. Приведем примеры
наиболее распространенных расстояний
и мер близости, характеризующих взаимное
расположение отдельных групп объектов.
Пусть
— t-я
группа (класс, кластер) объектов,
— число объектов, образующих группу
,
вектор
— среднее арифметическое объектов,
входящих в группу
(другими словами
— “центр тяжести” t-й
группы), a
— расстояние между группами
и
.
Наиболее распространенными методами определения расстояния между кластерами и являются: метод “ближайшего соседа” (1), метод “дальнего соседа” (2), метод оценки расстояния между центрами тяжести (3). Графическое представление оценки расстояния различными методами приведено на рис. 7.5.
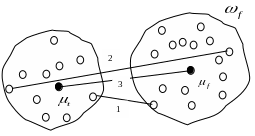
Рис. 7.5. Расстояния между классами (1 - метод “ближайшего соседа”, 2 - метод “дальнего соседа” 3 - метод оценки расстояния между центрами тяжести)
Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров:
(7.14)
Расстояние дальнего соседа — расстояние между самыми дальними объектами кластеров:
(7.15)
Расстояние центров тяжести равно расстоянию между центральными точками кластеров:
(7.16)
Обобщенное (по Колмогорову) расстояние между классами, или обобщенное k - расстояние, вычисляется по формуле
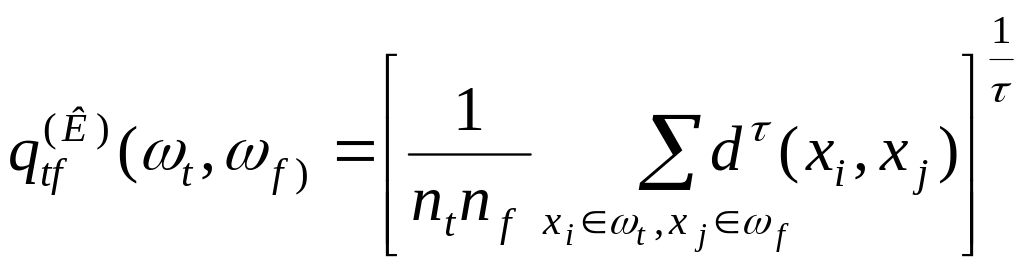(7.17)
Выбор той или иной меры расстояния между кластерами влияет, главным образом, на вид выделяемых алгоритмами кластерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную структуру. Расстояние дальнего соседа применяется, когда искомые группировки образуют в пространстве признаков шаровидные облака. И промежуточное место занимают алгоритмы, использующие расстояния центров тяжести и средней связи, которые лучше всего работают в случае группировок эллипсоидной формы.
7.3. Иерархический метод классификации
Среди всех методов
классификации самым распространенными
являются иерархические агломеративные
методы. Основная идея этих методов
состоит в том, что на первом шаге каждый
объект выборки рассматривается как
отдельный кластер. Иерархическая
процедура состоит в пошаговом объединении
наиболее близких классов. Близость
классов оценивается по матрице расстояний
или матрице сходства. На первом шаге
матрица сходства имеет размерность
.
На следующем шаге при объединении двух
классов матрица сходства пересчитывается.
Размерность матрицы сокращается на
единицу и становится
).
Процесс завершается за
шагов, когда все объекты будут объединены
в один класс. Заметим, что при расчете
матрицы сходства на очередном шаге
необходимо пересчитать только один
столбец и строку матрицы. Расстояние
между классами может быть рассчитано
различными способами (см. предыдущий
параграф).
Процесс объединения объектов можно изобразить в виде графа-дерева (дендрограммы). На дендрограмме указываются номера объединяемых объектов и расстояния, при которых произошли объединения. При выделении классов руководствуются скачками метрики сходства на дендрограмме.
Рассмотрим пример
решения задачи классификации с помощью
иерархического агломеративного
алгоритма. Расчеты были выполнены на
основании данных таблицы (рис. 7.6).
Диаграмма рассеивания признаков
представлена на рис. 7.7. На диаграмме
визуально выделяются три класса.
Убедимся, на примере, как объединит
объекты в классы, рассматриваемый
алгоритм.
Рис. 7.6. Таблица данных
Рис. 7.7. Диаграмма рассеивания признаков
На первом шаге рассчитывается матрица расстояний между объектами (евклидовы расстояния рис. 7.8). Матрицу расстояний рассчитываем с помощью макроса “Расстояния”. В матрице расстояний мы заменили диагональные элементы (нулевые значения) на значение заведомо большее, чем все остальные элементы матрицы (в нашем случае 100). Такая замена удобна для расчета минимального значения матрицы с помощью функции МИН.
Находим минимальное значение матрицы расстояний (1,414). Объединим объекты 1-2 в один класс. В новой матрице необходимо рассчитать расстояния от класса (1-2) до всех остальных объектов. Расстояние будем рассчитывать по методу ближайшего соседа. Для этого из двух расстояний рис. 7.9 необходимо выбрать минимальные значения. В результате будет получена новая таблица – рис. 7.10.
Рис. 7.8. Матрица расстояний (Шаг 1)
Рис. 7.9. Расчет расстояний от класса (1-2) до всех остальных объектов
Рис. 7.10. Матрица расстояний (Шаг 2)
Далее процесс объединения классов продолжается. На рис. 7.11 приведены расчеты при выполнения алгоритма на шагах 3-11. Процесс объединения объектов представлен на дендрограмме рис. 7.12. По дендрограмме можно обнаружить, что на определенном этапе происходит скачек расстояния, объединяемых классов. Этот скачек согласуется с классификацией объектом при визуальном анализе диаграммы рассеивания объектов. Студентам предлагается повторить расчеты, используя при расчете расстояний между классами объектов ”метод дальнего соседа”.
Рис. 7.11. Расчет матриц расстояний на шагах 7-11
Рис. 7.12. Дендрограмма объединения объектов