6.2. Сглаживание эмпирических данных теоретической функцией плотности ( )

Часто выборочный частотный ряд оказывается очень близким к какому-либо известному теоретическому закону распределения. Кроме того, отдельные методы анализа данных требуют того, чтобы данные подчинялись определенному закону распределения. В этих случаях возникает необходимость решения задачи проверки согласованности данных с теоретическим законом распределения. Критерии проверки статистических гипотез о согласованности данных с теоретическим законом распределения называются критериями согласия. Одним из самых распространенных критериев согласия является критерий согласия К. Пирсона (или - “хи квадрат”). В качестве меры расхождения теоретического и выборочного законов распределения в критерии принята взвешенная сумма квадратов отклонений соответствующих частотных рядов:

, (6.1)

где - теоретические вероятности попадания случайной величины в заданные интервалы ;

- частоты выборочного частотного ряда ;

k – количество интервалов частотного ряда;

n – объем выборки.

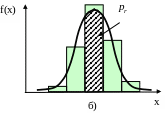
Рис. 6.4. Соотношение выборочного и теоретического частотных рядов: а) выборочная частота; б) – теоретическая частота

В теории доказывается, что если частотные ряды отличаются не значимо, то статистика (6.1) распределена по закону с степенями свободы, где k – количество интервалов, t – число связей (параметров, рассчитанных по выборке). Функция плотности имеет вид рис. 6.5. Проверка статистической гипотезы производится для правосторонней критической области. Уровень значимости обычно выбирают равным 0, 05.

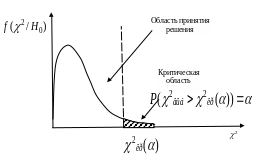
Рис. 6.5. Функция плотности распределения

Рассмотрим примеры проверки статистических гипотез о согласованности данных теоретическим законам распределения. Для этого будем использовать данные и результаты расчетов, приведенные в параграфе 3.2. Скопируем данные и таблицы выборочных частотных рядов на новый лист EXCEL (рис. 6.6 и рис. 6.7).

Рис. 6.6. Таблица данных

Рис. 6.7. Результаты предварительного анализа данных

Данные, приведенные в таблице данных на рис. 6.6 были получены путем моделирования. Признаки моделировались, как выборки из равномерных распределений, а признаки , как выборки из нормальных распределений. Проверим статистические гипотезы о том действительно ли модельные данные согласуются с теоретическими законами распределения (равномерным и нормальным), то есть, правильно ли мы решили задачу моделирования.

Рассчитаем теоретические частоты для равномерного распределения. Частоты теоретического частотного ряда по всем пяти интервалам (рис. 6.8).

Рис. 6.8. Теоретические вероятности равномерного распределения

Расчеты выборочных значений критерия для признаков приведены на рис. 6.9. В последнем столбце таблицы на рис. 6.9 содержатся критические значения критерия при степенях свободы .

Рис. 6.9. Расчет выборочных значений критерия для равномерных распределений

По результатам сравнения выборочных и критических значений критерия , приведенных на рис. 6.9 можно сделать вывод, что признаки не согласуются с гипотезой о равномерном распределении, а выборочные данные признака согласуются с гипотезой о равномерном распределении. Гистограммы, построенные по данным выборок признаков , так же подтверждают сделанный вывод. Совпадение результатов расчетов выборочных значений критерия для признаков не случайно. Признак был получен путем линейного преобразования признака .

Рассмотрим расчеты, произведенные для проверки гипотезы нормальности выборок признаков . Расчет теоретических частот приведем на примере признака . Теоретические частоты для нормального распределения производятся с помощью функции EXCEL НОРМРАСП. Функция НОРМРАСП позволяет рассчитать интеграл нормального распределения Рис. 6.10. Интерфейс функции НОРМРАСП приведен на рис. 6.11.

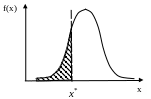
Рис. 6.10. Интегральная функция НОРМРАСП

Рис. 6.11. Ввод параметров функции НОРМРАСП

Расчет теоретических частот нормального распределения по интервалам производится в два шага. На первом шаге рассчитываются интегральные функции по правым границам интервалов. Последняя граница берется равной бесконечности и соответственно интеграл равен 1 (рис. 6.12). В числе параметров функции НОРМРАСП вводятся средние значения и среднеквадратичные значения, рассчитываемы по выборочным данным (рис. 6.7).

Рис. 6.12. Таблица накапливаемых частот нормальных функций распределения

На втором шаге рассчитываются вероятности попадания нормальных случайных величин с заданными параметрами на интервалы, построенные для частотных рядов выборочных данных. Вероятности рассчитываются как разности двух последовательных накапливаемых интегралов (рис.6.13).

Рис. 6.13. Таблица накапливаемых частот нормальных функций распределения

Рис. 6.14. Расчет выборочных значений критерия для нормальных распределений