Изложение численного метода

Дифференциальное уравнение нестационарной теплопроводности в случае одномерной задачи имеет вид

. (1)

В лабораторной работе №2 был изложен способ решения дифференциального уравнения теплопроводности (1) методом конечных разностей по явной схеме. Как было указано, решение задач по явной схеме будет устойчивым, если выполняется условие

. (2)

Последнее условие весьма обременительно. Как показывают практические расчеты, при достаточно малых ∆х и конкретных значениях а величина ∆τ оказывается очень малой и приходится медленно продвигаться по времени, т.е. делать большое число шагов по времени τ. Все это чрезвычайно повышает трудоемкость решения.

Рассмотрим теперь принципиально другое сеточное уравнение. Если взять приближенное значение производной по времени «назад» (см.рис.1.),

Рис.1. Пространственно-временная область одномерной задачи теплопроводности

то получим следующее конечно-разностное соотношение:

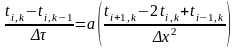. (3)

Уравнение (3) решается труднее, поскольку в него входят три неизветные температуры: Поэтому в данном случае нужно решать сразу всю систему разностных уравнений типа (3) для всех точек i,k сетки. Здесь так же, как и при решении уравнения Лапласа методом сеток, можно применить метод итераций.

Неявные разностные уравнения решаются сложнее, чем явные, но они абсолютно устойчивы при любом шаге по времени. Это позволяет выбирать шаг ∆τ значительно большим, чем в явных схемах, и соответственно уменьшать общее время счета всей задачи. Для реализации численного метода решения задач теплопроводности на ЭВМ разработан специальный метод прогонки, более эффективный, чем метод итераций.

Изложим метод прогонки на примере предыдущей задачи, предложенной в лабораторной работе №2. Уравнение (3) можно, очевидно, записать еще и в виде

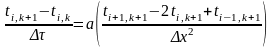(4)

при начальных и граничных условиях:

в момент времени k=0

, (5)

и задана в точках: i=1,2,…,n-1;

(6)

. (7)

Уравнение (4) для удобства дальнейших выводов запишем в виде

, (8)

где .

Представим чисто формально связь между 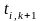и в виде

, (9)

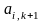где и некоторые коэффициенты, подлежащие определению. Если они будут известны, то делая «прогонку» в направлении справа-налево, начиная с правого граничного условия , можно по (9) последовательно найти все температуры в (k+1)-м слое по времени. Из (9), заменяя i на i-1, имеем

. (10)

Подставляя (10) в формулу (8), получим

. (11)

Отсюда

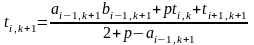. (12)

Сравнивая (12) с (9), получим следующие рекуррентные формулы:

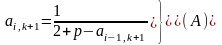(13)

При i=1 из (8) найдем

. (14)

Или, используя граничное условие (6), из (14) получим

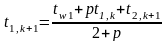. (15)

С другой стороны, из (9) найдем

. (16)

Сравнивая (16) и (15), получим

(17)

Пользуясь формулами (А) и (В), производя «прогонку» слева-направо в прямом направлении, последовательно найдем все коэффициенты .

Затем, используя «обратный ход», т.е. прогонку справа-налево, начиная с , как уже было указано, по (9) найдем все температуры в (k+1) слое, если известно распределение температур в k-м слое. Таким образом, указан переход от k-го слоя по времени к (k+1) слою.

Следовательно, отправляясь от известного начального (нулевого) слоя, можно построить решение во всех точках сетки i,k.