Министерство образования и науки Российской Федерации

Кубанский государственный технологический университет

Кафедра «Кадастра и геоинженерии»

З А Д А Н И Е

к контрольной работе

по дисциплине «Метрология, стандартизации, сертификация»

для студентов ЗФО, 120700 – Землеустройство и кадастры

Содержание задания:

Задача № 1

Определить результат многократного прямого измерения уклона дорожного покрытия по следующим исходным данным:

Коэффициент заложения откоса	Поправка
23-24-27-22-24 29-22-25-27-23 24-24-25-26-28 27-29-21-21-26 23-28-27-24-27 23-24-22-22-25	1

Задача № 2

Обработать результаты метрологической аттестации полевого курвиметра КП-302 по следующим исходным данным:

Измеренное расстояние, м	Нормативное значение длины, м
44,9-45,1-45,3-46,0-46,1	45

Задача №3

Обработать результаты измерения твердости дорожного покрытия и исключить аномальные по следующим исходным данным:

Количество ударов	Тип грунта	W
27-24-27-22-24 29-22-25-27-25	суглинки	1,00

Задача №4

Исключить систематические погрешности в процессе измерения массы предмета способами замещения и противопоставления по следующим исходным данным:

Масса гири, кг	Левое плечо – L1, м	Правое плечо – L2, м
1,45	0,29	0,33

Задача №5

Описать принцип работы, метрологические характеристики, привести рисунок (схему) следующего прибора для определения транспортно-эксплуатационных показателей автомобильных дорог: Установка динамического нагружения

Задача №6

Описать основные положения и разделы, а также область применения следующего норма-тивно-технического документа: ОСТ 218.1.002-2003 Автобусные остановки на автомобильных дорогах. Общие требования

Срок сдачи контрольной работы на кафедру __________________________________________

Руководитель работы: ____________________________________________________________

Задача №1

Многократные измерения

Многократные измерения характеризуются превышением числа измерений количества измеряемых величин. Обычно минимальное число измерений в данном случае больше трех. Одним из основных преимуществ многократных измерений является значительное снижение влияний случайных факторов на погрешность измерения.

Многократные измерения одной и той же величины постоянного размера производятся при повышенных требованиях к точности измерений. Наличие такого массива экспериментальных данных позволяет получить информацию о законе распределения вероятности результата многократного измерения.

Используя статистические методы обработки полученных данных, можно определить среднее значение результата измерения, а по правилу «трех сигм» исключить из массива ошибочные данные.

Уклономер КП – 206 предназначен для измерения поперечных уклонов дорожного полотна с асфальтобетонным покрытием.

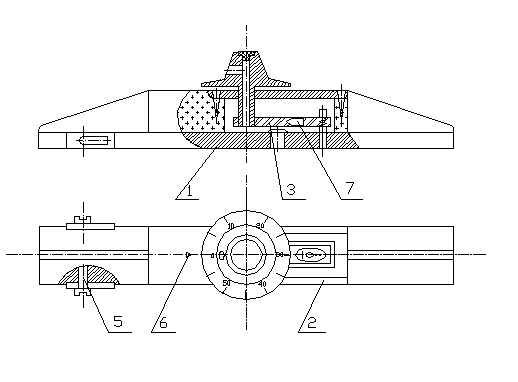
Основание 1 служит для установки прибора на дюралевой рейке при производстве замеров. Для предотвращения смещения уклономера при измерении на основании 1 смонтированы четыре фиксатора 5. Рычаг с установленным винтом 3 служит для изменения положения ампулы уровня 7. Ручка с лимбом 4 служит для поворота рычага 3 и фиксации показаний уклономера.

Измерение поперечного уклона дорожного покрытия происходит следующим образом. Устанавливается дюралевая рейка на дорожное покрытие в месте замера уклона. Место, где производится замер, не должно иметь выбоин, рытвин или бугров, способных исказить результаты измерений. После установки уклономера на рейку опускают фиксатор 5. Ручкой 4 добиваются установки ампулы уровня 7 в горизонтальное положение. По лимбу снимают отчет показания прибора. Замер производят не менее 30 раз.

Порядок решения задачи.

1. Значения поперечного уклона дорожного покрытия заносят в таблицу.

2. 2.Таблица 1 – значение поперечного уклона дорожного покрытия

Номер измерения	1	2	3	4	5	6	7	8	9	10
х	21	22	26	22	25	30	22	25	27	23
Q = xi + δ	24	25	29	25	28	33	25	28	30	26
Номер измерения	11	12	13	14	15	16	17	18	19	20
х	24	24	25	26	28	28	29	21	21	26
Q = xi + δ	27	27	28	29	31	31	32	24	24	29
Номер измерения	21	22	23	24	25	26	27	28	29	30
х	24	28	29	24	27	27	24	27	29	29
Q = xi + δ	27	31	32	27	30	30	27	30	32	32

Определим поправку δ прибора. Внесем поправку и получим 30 независимых результатов согласно таблице 1.

Определить диапазон значений

∆ Q = Q_max – Q_min

∆ Q = 33-24=9

Разделим диапазон «К» интервалов (разрядов). При числе изменений 30 – 100 рекомендуемое число интервалов от 7 до 9, отсюда

∆ Q* = ∆ Q/ К

∆ Q* = 9/8=1,125

Определим количество «n_i» измеренных значений Q, приходящихся на один разряд и занести в таблицу 2.

Таблица 2 - n_i – измеренных значений Q

Разряд	Q	ni
1	24 – 25,125	6
2	25,125-26,25	1
3	26,25-27,375	5
4	27,375-28,5	3
5	28,5-29,625	3
6	29,625-30,75	4
7	30,75-31,875	3
8	31,875-33	5
		Σ 30

Найдем частоту, соответствующую каждому разряду по формуле: m_i= n_i / Σn_i

m1 = 6/30=0,2		m5 = 3/30=0,1
m2 = 1/30=0,03		m6 = 4/30=0,13
m3 = 5/30=0,16		m7 = 3/30=0,1
m4 = 3/30=0,1		m8 = 5/30=0,16

Построим статистический ряд и оформим его графически в виде гистограммы. Для этого по оси абсцисс отложить разряды и на каждом из разрядов построить прямоугольник, в качестве высоты которого взять величину h_i , определяемую по формуле: h_i = m_i : ∆ Q*

h1 = 0,2/1,125 = 0,17	h5 = 0,1/1,125 = 0,08
h2 = 0,03/1,125 = 0,02	h6 = 0,13/1,125 = 0,11
h3 = 0,16/1,125 = 0,14	h7 = 0,1/1,125 = 0,08
h4 = 0,1/1,125 = 0,08	h8 = 0,16/1,125 = 0,14

После построения гистограммы соединяют отрезками прямых середины верхних сторон прямоугольников, получая при этом ломанную линию называемую полигоном.

Определим среднее значение Q_iв каждом разряде по формуле:

Q_i = Q_min + 0,5 ∆ Q* + (К – 1) ∆ Q*

Q1 =24+0,5*1,125 +(1-1) *1,125 = 24,56	Q5 = 24+0,5*1,125 +(5-1) *1,125 =29,05
Q2 = 24+0,5*1,125 +(2-1) *1,125 =25,68	Q6 = 24+0,5*1,125 +(6-1) *1,125 =30,18
Q3 = 24+0,5*1,125 +(3-1) *1,125 =26,81	Q7 = 24+0,5*1,125 +(7-1) *1,125 =31,30
Q4 = 24+0,5*1,125 +(4-1) *1,125 =27,93	Q8 = 24+0,5*1,125 +(8-1) *1,125 =32,43

Q_ср =24,56+25,68+26,81+27,93+29,05+30,18+31,30+32,43/8 = 28,49

Определим среднее квадратическое отклонение:

G=√(Q_i-Q_ср)²/к-1=√3,93*2² +2,81*2² + 1,68*2² +0,56*2² /8-1=±2,75

24,56-28,49 = - 3,93	5. 29,05-28,49 = 0,56
25,68-28,49 = -2,81	6. 30,18-28,49 = 1,68
26,81-28,49 = - 1,68	7. 31,30-28,49 = 2,81
27,93-28,49 = -0,56	8 . 32,43-28,49 = 3,93