
- •Вопрос №16
- •Вопрос №17
- •Вопрос 21
- •Прямая в r2, ур-е прямой( векторное, общее, ур-е прямой, проход-ей через данн точку перепенд-ой данному вектору)
- •Вопрос №22
- •Вопрос 26. Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности х2 и у2-координаты центра
- •5.Эллипс может быть получен сжатием окружности.
- •Вопрос№31 Расстояние от точки до плоскости. Угол между плоскостями
- •Вопрос№37
- •Предел функции на бесконечности и в точке. Односторонние приделы.
- •Теорема Ферма, теорема Ролля. Их геометрический смысл.
Вопрос№37
Понятие
функции. Способы задания функции,
операций над ними. Обратная функция.
Элементарные функции, их классификация.Функцией
называется закон, по которому числу х
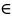 Х,
поставлено в соответствие только одно
число у, пишут
Х,
поставлено в соответствие только одно
число у, пишут
![]() ,
при этом x называют аргументом функции,
y называют значением функции.способы
задания функций:1.
АналитическийЗаключается он в том, что
функция задается формулой, устанавливающей,
какие операции нужно произвести над х,
чтобы найти у. Например
,
при этом x называют аргументом функции,
y называют значением функции.способы
задания функций:1.
АналитическийЗаключается он в том, что
функция задается формулой, устанавливающей,
какие операции нужно произвести над х,
чтобы найти у. Например
 .2.
ТабличныйТабличный способ наиболее
удобен, когда множество Х конечно. При
этом способе составляется таблица, в
которой каждому элементу из множества
Х, ставится в соответствие число
Y.
Пример:
.2.
ТабличныйТабличный способ наиболее
удобен, когда множество Х конечно. При
этом способе составляется таблица, в
которой каждому элементу из множества
Х, ставится в соответствие число
Y.
Пример:
x |
3 |
5.1 |
10 |
12.5 |
13 |
20 |
y |
9 |
23 |
90 |
110 |
112 |
300 |
3.ГрафическийПри
графическом способе вводится прямоугольная
система координат и в этой системе
координат изображается множество точек
с координатами (x,y). При этом
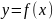 .Функцию
называют обратной
функцией по отношению к функции y=f(x).
Функция y=f(x)
и y=
f-1(x)
называют взаимообратными.Элементарные
функции 1.степенные
у
.Функцию
называют обратной
функцией по отношению к функции y=f(x).
Функция y=f(x)
и y=
f-1(x)
называют взаимообратными.Элементарные
функции 1.степенные
у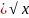 y=x-1
и
т.д.
y=x-1
и
т.д.
2. показательные y = ax3.логарифмические y = logax4. тригонометрические y = sinxy = cosx и т.д.5. обратные тригонометрические. y = arcsinxy = arccosx и т.д.
Вопрос№38
Предел функции на бесконечности и в точке. Односторонние приделы.
Число
А назыв. пределом функции y=f(x)
при x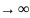 ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа
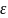 найдется такое число S>0,
что для всех x
таких что модуль x>S
выполн. Неравенство модуль F(x)-A<
найдется такое число S>0,
что для всех x
таких что модуль x>S
выполн. Неравенство модуль F(x)-A<
A=limx->x0f(x)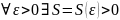
Число
А называется пределом функции
![]() в
точке x
в
точке x х0(или
или в точке x0
),
если для любой сколь угодно малого
полож. числа
найдется такое полож. число
х0(или
или в точке x0
),
если для любой сколь угодно малого
полож. числа
найдется такое полож. число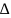 зависящее от
,
что для всех x
зависящее от
,
что для всех x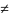 x
и таких, что /x-x0/<
выполняется неравенство /f(x)-A/<
.Различают
правый односторонний придел и левый
односторонний придел:Число
x
и таких, что /x-x0/<
выполняется неравенство /f(x)-A/<
.Различают
правый односторонний придел и левый
односторонний придел:Число
![]() называется
правым
односторонним пределом функции
называется
правым
односторонним пределом функции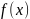 в точке
в точке
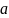 ,
если для
,
если для
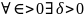 такое, что для любого
такое, что для любого
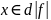 и
и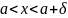 ,
выполняется неравенство
,
выполняется неравенство
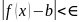 .
Правый предел обозначается
.
Правый предел обозначается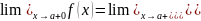 Число
называется
левым
односторонним пределом функции
в точке
,
если для
такое, что для любого
и
Число
называется
левым
односторонним пределом функции
в точке
,
если для
такое, что для любого
и и, выполняется неравенство
.
Левый предел обозначается
и, выполняется неравенство
.
Левый предел обозначается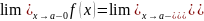
Вопрос№39
Основные теоремы о пределах. Замечательные пределы
Теоремы:1.
Если предел F(x)
сущ., то он единственный.2. Придел суммы
limx->x0(f(x)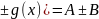 3.
lim
3.
lim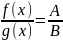 g(x)
g(x)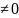 ;
B
;
B
4.limx->x0(c*f(x))=c*A5.
limx->x0
(f(x)*g(x))=A*B6. Если
предел limx->x0f(x)=ALimu->A limx->x0
limx->x0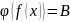 7.Если
в некоторой окрестности в точке x0
f(x)<g(x),
то limx->x0
f(x)
7.Если
в некоторой окрестности в точке x0
f(x)<g(x),
то limx->x0
f(x)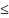 limx->x0
g(x)8.
Если f(x)
h(x)<g(x),при
чем придел f(x)равен
g(x
)u=A,
то придел h(x)
тоже равен А. . limx->x0f(x)=
. limx->x0g(x)=A
.
limx->x0h(x)=AЗамечательные
приделы:Первый
замечательный предел:
limx->x0
g(x)8.
Если f(x)
h(x)<g(x),при
чем придел f(x)равен
g(x
)u=A,
то придел h(x)
тоже равен А. . limx->x0f(x)=
. limx->x0g(x)=A
.
limx->x0h(x)=AЗамечательные
приделы:Первый
замечательный предел: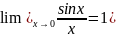
Второй замечательный предел:
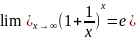
Вопрос№40
Непрерывность функции в точке. Точки разрыва и их классификация.
Функция y=f(x) назыв. непрерывной в точке х0 , если она удвол. Условию: 1. Опр. в этой точке. 2. Имеет конечный предел x х0 . 3.предел равен значению функции 1 в этой точкеlimf(x)=f(x0)
Определение limf(x)( x х0)=f(limx)( x х0)
Функция y=f(x) назыв. непрерывной в точке х0 , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
lim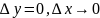
x0- назыв. точкой разрыва функции f(x), если точка функции не явл. непрерывной, т.е нарушено хотя бы одна из трёх условий непрерывности.
Точки разрыва: 1. Точки разрыва первого рода: это когда сущ. Конечные односторонние приделы слева и справа не равные друг другу. 2. Точки разрыва второго рода: когда хотя бы один из односторонних приделов (слева или справа) или не существует или равен бесконечности.
Вопрос№41
Св-ва ф-ции непрерывных в точкею Непрерывность ф-ции на промежутке Св-ва ф-ции, непрерывность на отрезкеТеорема Вейерштрасса: Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.Теорема о промежуточных значениях: Если функция y=f(x) непрерывна на отрезке [a;b] и принимает на его концах неравные значения f(a)=A и f(b)=B, то на этом отрезке она принимает все промежуточные значения между A и B.Непрерывность функции на промежутке Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка). При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Вопрос№42
свойство функций непрерывных на отрезке
1)Теорема
Вейерштрасса. Если функция непрерывна
на отрезке, то она достигает на этом
отрезке свои наибольшее и наименьшее
значения.2) Непрерывная на отрезке [a;b]
функция является ограниченной на этом
отрезке.3) Теорема Больцано-Коши. Если
функция y=f
(x)
является непрерывной на отрезке [a;b]
и принимает на концах этого отрезка
неравные между собой значения, то есть
f
(a)=
a0,
,f
(b)=
b0
, то на этом отрезке функция принимает
и все промежуточные значения между a0
и b0
.4)Если функция y=f(x),
которая непрерывна на некотором отрезке
[a,b],
принимает на концах отрезка значения
разных знаков, то существует такая
точка c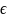 [a,b]
такая, что f(c)=0
.
[a,b]
такая, что f(c)=0
.
Вопрос№43
производная
функция. Механический,экономический
и геометрический смысл производной.
Эластичность функции её экономические
приложениеПроизводной
функции f(x) (f'(x0)) в точке x0 называется
число, к которому стремится разностное
отношение
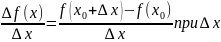
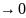 Геометрический
смысл
производной. Производная в точке x0
равна угловому коэффициенту касательной
к графику функции y=f(x) в этой точке f
‘ (x0
)=tg>0Механический
смысл Пусть
задан путь s=f(t)
движения материальной точки. Скорость
данной материальной точки в момент
времени t
есть производная от пути s
по времени t:
v(t)=S
‘(t)S=S(t)-уравнение
пути движенияЭкономический
смысл производной:
производительность труда есть производная
объема произведенной продукции по
времени. μ=μ(t)-обьем
произведенной продукции за период
времени t
Геометрический
смысл
производной. Производная в точке x0
равна угловому коэффициенту касательной
к графику функции y=f(x) в этой точке f
‘ (x0
)=tg>0Механический
смысл Пусть
задан путь s=f(t)
движения материальной точки. Скорость
данной материальной точки в момент
времени t
есть производная от пути s
по времени t:
v(t)=S
‘(t)S=S(t)-уравнение
пути движенияЭкономический
смысл производной:
производительность труда есть производная
объема произведенной продукции по
времени. μ=μ(t)-обьем
произведенной продукции за период
времени t
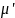 (t)-производительность
трудаОпределение
(эластичность).
Эластичностью функции Ex(y) называется
величина Ex(y)=
(t)-производительность
трудаОпределение
(эластичность).
Эластичностью функции Ex(y) называется
величина Ex(y)= *y’Смысл:
если переменная Х получит приращение
на 1%, то зависимая переменная получит
приращение на х(у)% где Х-выпуск продукции,
а у-себестоимость ед. продукции.
*y’Смысл:
если переменная Х получит приращение
на 1%, то зависимая переменная получит
приращение на х(у)% где Х-выпуск продукции,
а у-себестоимость ед. продукции.
Вопрос№44
правила дифференцирования таблица производных
Правило дифференц.

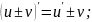
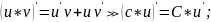
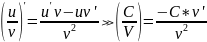
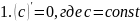

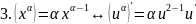


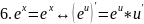

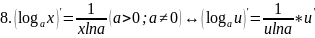
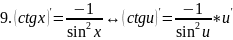

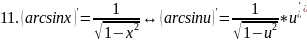
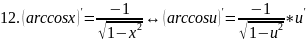
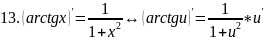
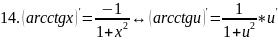
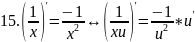
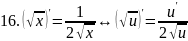

Вопрс№45
производная показательной неявной функции. производные высших порядков.
Если независимая переменная x и y функция связаны уравнением вида F(x,y)=0, которое не разрешено относительно y, то функция y называется неявной функцией переменной .xПроизводная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у"Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:y(n)=(y(n-1))¢ .Производные порядка выше первого называются производными высших порядков.Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уν или у(5)— производная пятого порядка). вопрос№46
