Вопрос 26. Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности х2 и у2-координаты центра

Вопрос №27

27. Эллипс - это геометрическая фигура, которая ограничена кривой, заданной уравнением  Фокусное расстояние и полуоси связаны соотношением: а2=в2+с2 Свойства : 1.Эллипс пересекает каждую из осей координат в двух точках.2.Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.3.Эллипс имеет две взаимно перпендикулярные оси симметрии

4.Эллипс имеет центр симметрии.

5.Эллипс может быть получен сжатием окружности.

Вопрос№28

Гипербола, ее характеристики, геометрические свойстваГ.—это геометр место тчек плоскости, для кот-ых модуль разности расстояний от 2х заданн точек есть величина постоянн( и равна 2а). , каноническое ур-е гиперболы где b ² =a ² +c ². а наз-ют действит-ой полуосью гиперболы, число b - мнимой полуосью. гипербола симметр относ-но осей координат и, след-но, относ-но начала координат. Т.к. из канонич ур-я гиперболы следует, что то нет точек кривой в полосе -a > x > a.при   ветви гиперболы неогран-но приближ-ся к прямым  , не пересекая их.Число  , кол-но характер-ее сжатие ветвей наз-ют эксцентриситетом гиперболы. Точки перес-я гиперболы с действ-ой осью наз-я вершинами гиперболы.2 прямые  наз-ют директрисами.

Вопрос №29.

Параболой наз.геометрическое место точек плоскости,для к-х расстояние от заданной точки (F) до заданной прямой директрисы есть величина постоянная.Исходя из определения расстояние от точки M до директрисы MK=MF,где MF=(x-p/2)²+y²=MK=x+p/2x²-px+p²/4+y²-x²-px-p²/4=0y²=2px -Каноническое уравнение параболы,ориентированной вдоль Оx,где p>0аналагично получено x²=2py вдоль ОyF (p/2;0)-в первом случае x=-p/2;F(0;p/2)-во 2-ом случае y=-p/2;Для эллипса эксцентриситет 0<E<1Для гиперболы E>1Для параболы E=1;

Вопрос №30.

Общее уравнение плоскости имеет вид , где коэффициенты A,B,C одновременно не равны нулю.угол между плоскостями находится по формуле: На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей. Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если: =0Плоскости параллельны, векторы нормалей коллинеарны: ïï .Это условие выполняется, если:

Вопрос№31 Расстояние от точки до плоскости. Угол между плоскостями

Угол γ между плоскостями A1x+B1y+C1Z+D1=0 и A2x+B2y+C2Z+D2=0 определяется по формулеCosγ=(A1*A2+B1*B2+C1*C2)/√A1²+B1²+C1²*√A2²+B2²+C2² (эти суммы под корнем)Расстояние от точки М0(x0,y0,z0) до плоскости Ax+By+Cz=Dd= |Ax0+By0+Cz0+D|/√A²+B²+C²

Вопрос №32

Пр линия в пр-ве.Параметрич ур-е прям.Канонич ур-е пр

1-это точка M0(x0,y0,z0)2-это точка M(x,y,z)вектор M0M=(x-x0;y-y0;z-z0)векторы M0M//S(x-x0)/k=(y-y0)/e=(t-t0)/m это каноническоеВведем параметр t Є R и положим (x-x0)/k=(y-y0)/e=(z-z0)/m=t, t Є R x=x0+kt y=y0+et это все параметрич ур-я прямой в пр-ве z=z0+mtУр-я вида A1x+B1y+C1Z+D1=0 это общие ур-я A2x+B2y+C2Z+D2=0 прямой в пространствеОни задают прямую ,как линию пересечения 2-х пл-тей Взаимное расположение прямой и пл-ти в пр-веПусть задана прямая каноническими ур-ми(x-x0)/k=(y-y0)/e=(t-t0)/mи плоскость общим ур-ем плоскости Ax+By+Cz+D=0 Дано:S=(k,e,m)-направленный вектор прямой N=(A,B,C) Cos(90-β)=sinβ=(N,S)/|N|*|S|=(Ak+Be+Cm)/√ ²+B²+C²√k²+e²+m² Условие парал-ти прямой к плоскости Ak+Be+Cm=0 Условие перпенд-ти Если пр перп-на пл-ти,то ее направл в-р S кол-н норм в-ру пл-ти S//N A/k=B/e=C/m Условие принадлежности прямой к плоскости:Ax0+By0+Cz0+D=0 Ak+Be+Cm=0

Вопрос №33

Понятие множества, объединение, пересечение, дополнение множества, числовые множества, интервал, полуинтервал Четкого определения не существует, Множ-во А содерж-ся в множ-ве В ,если каждый эл-т А есть Эл-т В ,если каждый эл-т А есть эл-т В, но не все эл-ты В есть эл-ты А, то А-подмнож-во В.(Включение) В-надмнож-во,Если ,то А-собсв-ое подмнож.Равные, если Операции Перес-е ,Объед-е .операц-я объедин-я коммутативна, объедин-я транзитивна,пустое множ-во Х явл-ся нейтральным эл-том операций. Полуинт-л-множ-во точек прямой, заключ-ых между тчками А и В, при этом одна из них не входит в полуинт-л.Интервал-множ-во тчк прямой между тчками А и В, причём сами А и В не причисл-ся к интервалу.

№ 34 ограниченые и неогр множества

Множ-во наз-ся огран-ым сверху, если все эл-ты множ-ва лежат левее С Множ-во наз-ся ограниченным, если

Вопрос №35

Понятие окрестности точки. Предельная, изолированная, внутренняя, внешняя точки множества. Открытые и закрытые множества.

Окрестность тчки-множ-во,содеж-ее данную точку, и близкие к ней. Внутренняя точка множ-ва-тчка, входящая в это множ-во вместе со своей окрестностью.Открытое множ-во –это множ-во, каждый эл-т которого входит в него вместе со своей окрестностью.

Вопрос №36

Придел числовой последовательности. Сходящиеся и расходящиеся последовательности. Бескон-но большие и бескон-но малые(б.м.) послед-сти; связь межу ними. Св-ва бесконечно малых и сходящихся последовательностей (сход. послед.). Предел последовательности(1+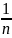 )ⁿ, при n Если каждому натуральному числу n поставлено в соответствии число x_n, , то говорят, что задана числовая последовательность (последовательность чисел) или просто последовательность x₁,x₂,…x_n.Последовательность, которая имеет предел, называется сходящейся; иначе - расходящейся.Последовательность a_nназыв. бесконечно большой, если предел lim а_n(n-> )= ,бесконечно малой lim а_n(n-> )=0.Св-ва бесконечно малых:1.Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность2.Произведение любого конечного числа б. м. последовательность есть б.м. последовательность3.Произведение ограниченной последоват. на б. м. есть последовательность б.м.Св-ва сход. послед.:1.Имеет единственный предел2.Всякая послед. сходящейся послед. сходится у тому же пределу.3.Сход. послед. Ограничена.4. 3. Если последовательность монотонна и ограниченна, то она сходится.5. если a_nb_nсход. послед.Причем limа_n(n-> )=a, lim а_n(n-> )=b, тоlimа_n + b_n=a , lim а_n * b_n(n-> )=a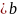 , lim c* c_n(n-> )=c*a(c=const)Рассмотрим последовательность (1+ )ⁿ, при n . Доказывается, что эта последовательность монотонная огранич. и возрастающая => имеет придел и этот придел обознач. е=2,718(Эйлерово число) т.е. предел (1+ )ⁿ(n =е