Вопрос №1 Матрицей

размера mxn наз-ся прямоуг-я табл чисел, содерж-я m строк и n столбцов. Вектор-строкой наз-т матрицу, сост-ую из 1 строки. Вектор-столбцом - из 1 столбца. Матрица, у которой кол-во столбцов равно кол-ву строк, наз-ся квадратной матрицей

Понятие матрицы, виды матрицы, примеры

ого порядка. Элементы матрицы, у которых номер строки и номер столбца совпадает, называются диагональными и образуют главную диагональ матрицы. Если все недиагональные элементы матрицы равны нулю, то матрицу называют диагональной. Если у диагональной матрицы n-ого порядка на главной диагонали все элементы равны 1, то матрица называется единичной и обозначается Е. Матрица любого размера, все элементы которой равны 0, называется нуль-матрицей, треугольная, трапециевидная, симметрическая.

Вопрос №2

Умножение матрицы на число, сложение матриц. Св-во операций сложения и умножения. Примеры

1)Умножение матрицы на число: условий нет, умножить на число можно любую матрицу. Произведением матрицы А на число  называется матрица В, равная А, каждый элемент которой находится по формуле: bij = x aij. Для того, чтобы умножить матрицу на число необходимо умножить на это число каждый элемент матрицы. 2)Сложение 2-х матриц: условие - складывать можно только матрицы одинакового размера. Суммой 2-х матриц А и В называется матрица С=А+В, каждый элемент которой находится по формуле Сij=aij+bij. Для того, чтобы сложить 2 матрицы, необходимо складывать между собой элементы, стоящие на одинаковых местах. 3)Вычитание 2-х матриц: операция аналогична сложению.

Вопрос №3

Умножение матриц. Транспонирование матриц. Примеры

Умножение 2-х матриц: умнож-е А на В возможно тогда и только тогда, когда число столбцов А равно числу строк В; произв-ем матрицы А размера mxk на матрицу В размера kxn наз-ся матрица С размера mxn, каждый эл-т которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие эл-ты j-ого столбца матрицы В. 5)Возведение в степень: возводить в степень можно только квадратные матрицы; целой полож-ой степенью квадратной матрицы Аm наз-ся произведение m-матриц, равных А. 6)Транспонирование: условий нет; трансп-ие-операция, в результате которой строчки и столбцы матрицы меняются местами с сохранением порядка элемента, при этом элементы главной диагонали остаются на своих местах.

Вопрос №4

Определитель матриц 1-ого, 2-ого, 3-ого порядков. Их вычисление. Примеры

Определитель- число, характеризующее матрицу. Определителем матрицы 1-го порядка А=(а11) является единственный элемент этой матрицы. Определителем 2-го порядка называется число, характеризующее матрицу 2-го порядка, которое находится по следующему правилу: из произведений элементов главной диагонали вычитается произведение элементов второй диагонали матрицы А. Определителем матрицы 3-го порядка называется число, вычисляемое по правилу Сарруса. Правило Сарруса: определитель 3-го порядка (3) равен алгебраической сумме 6-ти тройных произведений элементов, стоящих в разных строках и разных столбцах; со знаком «+» берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников, чьи основания параллельны главной диагонали, остальные слагаемые берутся со знаком «-».

Вопрос №5

Определитель квадратной матрицы n-го порядка. Теорема Лапласа. Примеры

Определитель квадратной матрицы n-ого порядка высчитывается рекуррентным способом, при этом используется понятие минора и алгебраического дополнения элемента матрицы. Теорема Лапласа: определитель квадратной матрицы равен сумме произведений элементов к.-л. строки или столбца на их алгебраические дополнения.

Вопрос №8

Минор r-го порядка матрицы. Базисный минор матрицы. Ранг матрицы и его свойства. Теорема о рангах матрицы. Вычисление ранга

Минором Мij квадратной матрицы n-го порядка для элемента аij называется определитель (n-1)-ого порядка, полученный с данного вычёркиванием i-ой строки и j-ого столбца.В матрице   размеров   минор r-го порядка называется базисным, если он отличен от нуля, а все миноры (r+1)-ro порядка равны нулю или их вообще не существует.Рангом матрицы А называется наивысший порядок отличных от 0 миноров этой матрицы rang A=r(A). Ранг матрицы не изменяется при проведении элементарных преобразований. Преобразования: 1)отбрасывание строки или столбца, состоящих из одних нулей; 2)умножение всех эл-ов к.-л. строки или столбца матрицы на одно и то же число, отличное от 0; 3)изменение порядка строк или столбцов матрицы; 4)прибавление к каждому эл-ту к.-л. строки или столбца эл-ов др. строки или столбца, умноженных на одно и то же число, не равное 0; 5) транспонирование матрицы

Вопрос №6

Свойства определителей

1) Если к.-л. строка или столбец в матрице состоит из одних нолей, то  этой матрицы равен 0. 2)При транспон-ии матрицы её определ-ль не измен-ся: А = А’ . 3) Если все эл-ты к.-л. строки или столбца матрицы умножить на одно и то же число, то и  этой матрицы умнож-ся на это же число. 4) При перестановке местами 2-х строк или столбцов матрицы её опр-ль меняет свой знак на противопол. 5) Если квадратная матрица содержит 2 одинак строки или столбца, то её опр-ль равен 0. 6)Если 2 строки или 2 столбца матрицы пропорц-ны, то её  равен 0. 7) Опр-ль матрицы не измен-ся если к эл-там 1ой строки или столбца прибавить эл-ты другой строки или столбца, умноженный на одно и то же число. 8)Если к.-л. столбец или строка матрицы представляет собой сумму 2-х элементов, то  этой матрицы может быть представлен в виде суммы 2-х определителей.

Вопрос №7

Обратная матрица. Теорема существования обратной матрицы. Ее вычисление

Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении её на заданную как справа так и слева получатся единичная матрица. Теорема (необходимое и достаточн.условие сущ-я обратн.матрицы): обратная матрица А-1 сущ-т и единственна тогда и только тогда, когда заданная матрица не вырожденная. Матрица называется вырожденной, если её определитель равен 0, в противном случае она – не вырожденная. Алгоритм: 1)Определитель заданной матрицы. 2)Транспонирование. 3)Алгебраические дополнения всех элементов транспонированной матрицы. 4) Присоед.матрица А (на месте каждого эл-та Ат его алгебраич.доп-я). 5) А-1= 1/А . 6) ПроверкаА-1 А=Е.

Вопрос №9

Система m-линейных уравнений с n неизвестными. Матричная запись системы. Метод обратной матрицы. Метод Крамера

Линейным ур-ем относительно неизв-ых x1,x2,…,xn наз-ся выражение вида a1x1+a2x2+…+anxn=b, где a1,a2,…,an и b- простые числа, причём a1,a1,…,an наз-ся коэффициентами при неизвестных, а b- свободным коэффициентом. Послед-сть чисел k1,k2,…,kn наз-ся решением ур-я, если при подстановке этих чисел в ур-е оно обращ-ся в верное рав-во. Два лин-ых ур-я наз-ся равносильными, если их решения совпадают. Чтобы получить равносил ур-е из заданного, необходимы следующие преобраз-я: 1) перенос слагаемых из одной части ур-я в другую; 2) поэлементное умножение всего ур-я на одно и то же число, отличное от ноля. Решить линейное ур-е –это значит найти все его решения или установить, что их нет. Система уравнений называется совместной, если она имеет хотя бы одно решение. Система ур-ий называется определённой, если она имеет одно единственное решение, и неопределённой, если решений множество. Неизвестное x1 называется разрешённым, если к.-н. ур-е системы содержит неизвестное x1 с коэффициентом, равным 1, а во все др. ур-я системы неизвестное x1 не входит. Если каждое ур-е системы содержит разрешённое неизвестное, то такую систему называют разрешённой. Неизвестные СЛУ, которые не входят в разрешённый набор, называются свободными. Разрешённая СЛУ всегда совместна, она будет определённой, если число ур-ий равно числу неизвестных; и неопределённой, если число неизвестных больше, чем ур-ий. Для того, чтобы определить совместна система или нет, не решая её, можно воспользоваться теоремой Кронекера-Капелли. Матрица, эл-тами которой являются коэффициенты при неизвестных системы, называется матрицей системы. Матрица системы, дополненная столбцом свободных коэффициентов, называется расширенной матрицей. Правило Крамера: пусть А-определитель матрицы системы, а j-определитель матрицы, полученной из матрицы системы заменой j-ого столбца на столбец свободных коэффициентов; тогда, если А0, то система имеет единственное решение, определяемое по формуле  Xj= j/ A.

Вопрос №10

Метод Гаусса. Эквивалентные преобразования системы. Базисные и свободные неизвестные. Критерий совместимости

Метод Гаусса: каждую СЛУ при помощи конечного числа преобразований можно превратить в разрешённую системы ур-ий или в систему, содержащую противоречивое ур-е. Противоречивым называется ур-е вида OX1+OX2+...+OXn=b. Если каждое ур-е системы содержит разрешённое неизвестное, то такую систему называют разрешённой. Неизвестное x1 называют разрешённым, если к.-н. ур-е системы содержит неизвестное x1 с коэффициентом, равным 1, а во все другие ур-я системы неизвестное x1 не входит. Если ранг системы меньше числа неизвестных и система разрешима, то решений получится множество. Это множество решений принято описывать специальным образом. Например, пусть имеется 3 неизвестных, а независимых уравнений только 2. Одно из неизвестных можно перенести (вместе с его коэффициентом) в правую часть (с обратным знаком, конечно), и объявить это неизвестное "свободным". Ему можно произвольно задавать любые значения, а оставшиеся два неизвестных будут единственным образом выражаться через правые части. Эти два неизвестных называются "базисными". Пример: x+y+z=2, x-y+z+3; x+y=2-z, x-y=3-z; Здесь z - свободное неизвестное, x,y - базисные неизвестные;Ответ: x=5/2-z, y=1/2Теорема Кронекера-Капелли: СЛУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы. Система ур-ий называется совместной, если она имеет хотя бы одно решение.

Вопрос №11

Системы линейных однородных уравнений. Фундаментальная система решений

Система m лин ур-ий с n переменными наз-ся системой линейных однородных ур-ий, если все своб-ые члены равны 0. Система лин однород ур-ий всегда совместна, т.к. она всегда имеет,хотя бы, нулевое реш-е. Система лин однород ур-ий имеет ненул-е реш-е тогда и только тогда, когда ранг её матрицы коэффициентов при переменных меньше числа переменных, т.е. при rang A  n. Всякая лин. комбинация решений системы лин. однородн. ур-ий также является решением этой системы. Система лин.независимых решений е1, е2,…,еk называется фундаментальной, если каждое решение системы является линейной комбинацией решений. Теорема: если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений меньше числа переменных n, то всякая фундаментальная система решений системы состоит из n-r решений. Поэтому общее решение системы лин. однордн. ур-ий имеет вид: с1е1+с2е2+…+сkеk, где е1, е2,…, еk – любая фундаментальная система решений, с1, с2,…,сk – произвольные числа и k=n-r. Общее решение системы m линейных ур-ий с n переменными равно сумме общего решения соответствующей ей системы однородн. линейных ур-ий и произвольного частного решения этой системы.

Вопрос №13

Векторы на плоскости и в пространстве. Линейные операции над векторами, их св-ва. Базис их плоскости и в пространстве. Ортонормированный базис

Система n—мерных лин. независимых векторов называется базисом Rn (R2-плоскость,R3-пространство), если каждый вектор этого пространства R разлагается по векторам этой системы. Базисом называется совокупность всех лин. независимых векторов системы пространства. Теорема: для того, чтобы -- 1)2 вектора на плоскости (2)3-в пространстве) были линейно не зависимы необходимо и достаточно, чтобы они были не 1) коллиниарны (2) компланарны).  Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Вопрос №14

Необходимое и достаточное условие компланарности векторов. Скалярное произведение векторов и их св-ва. Критерий перпендикулярности векторов, угол между векторами, длина векторов

В математике исп-ся 2 вида величин: а) скалярные – величины, которые полностью определяются заданием их числовых значений (длина, площадь, объём, масса и т.д.); б) векторные – величины, для полного определения которых помимо числ-го значения треб-ся ещё и напр-ия в пространстве (изобр-ся при помощи векторов). Вектор – направленный отрезок на плоскости или в пространстве, имеющий определ длину, у которого одна из точек принята за начало, а другая за конец. Координатами вектора а явл-ся координаты его конечн точки. Длиной вектора (нормой) или модулем наз-ся число, равное длине отрезка, изобр-его вектор ax2+y2(+z2). Если начало и конец вектора совпадают, то такой вектор наз-ся нулевым и обозначается 0. ( напр-е 0 произвольно, не определено). Для каждого а, отличного от 0, сущ-ет противоположный -а, кот-ый имеет модуль, равн а, коллиниарен с ним, но напр-ен в др сторону. 2 вектора а ив наз-ся коллинеарными, если они расположены на 1ой прямой или на параллельных прямых. 2 вектора наз-ся равн, если они: 1)имеют равн модули; 2)коллиниарны; 3)напр-ны в одну сторону. Векторы наз-ся компланарными, если они лежат в одной плоскости или параллельны одной плоскости. 2 вектора а ив наз-ся коллинеарными, если они расположены на одной прямой или на параллельных прямых. Теорема: если диагональная система явл-ся частью n-мерных векторов, то она же является базисом этой системы. Теорема: любой вектор системы векторов единственным образов разлаг-ся по векторам её базиса.Скалярным произведением 2х вект-в   и   наз-ся ЧИСЛО, равное произведению длин этих векторов на косинус угла между ним

Вопрос №15

n-мерное векторное пространство. Аксиомы n-мерного векторного пространства. Скалярное произведение n-векторов, длина n-вектора. Примеры

N-мерным вектором наз-ся упорядоч-ая совокупность n-действительных чисел, записанных в виде x=(x1,x2,xi,xn), где Xi-компонента X. 2 N-мерных вектора равны тогда, когда равны их соответствующие компоненты: x =y, если xi=yi i. Множ-во векторов с действительными компонентами, в котором определ операции слож-я векторов и умнож-я вектора на число, удовлетв-ее всем св-вам суммы(коммутативное, ассоциативные), наз-ся векторным простр-ом. Размерность вект-го простр-ва равна кол-ву векторов в базисе этого простр-ва. Совок-сть n-мерных векторов, рассм-ая с определ-ми в ней операциями слож-я векторов и умнож-я вектора на число, наз-ся n-мерным координатным простр-ом. Система n—мерных лин. Незав-ых векторов наз-ся базисом Rn (R2-плоскость,R3-пространство), если кажд вектор этого простр-ва R разлаг-ся по векторам этой системы.

Вопрос №16

Линейная зависимость n-векторов. Критерий линейной зависимости системы n-векторов. Ранг. БазисСистема n—мерных лин. Незав-ых векторов наз-ся базисом Rn (R2-плоскость,R3-пространство), если кажд вектор этого простр-ва R разлаг-ся по векторам этой системы. Базисом наз-ся совокупность всех лин. Незав-х векторов системы простр-ва.Система векторов наз-ся лин-но зависимой, если сущ-ют такие числа α_1, α₂ .. α_m , из которых хотя бы 1 не =0, что Если среди векторов системы есть нул вектор, то система лин-но зависима.Если r векторов системы лин-но зависимы, то все m векторов лин-но зависимы.Для того, чтобы система была лин-но завис-й, необх-мо и достат-но, чтобы хотя бы 1из векторов лин-но выражался через остальные.Рангом системы векторов наз-ся число векторов в любом базисе системы, т.е.и ранг есть макс-ое число лин-но незав-х векторов системы. Следствие: Система, сост-ая более чем из n n-мерных векторов, лин-но зависима.Набор любых n лин-но независ векторов n-мерного векторного простр-ва наз-ся базисом этого простр-ва.

Вопрос №17

Линейные операторы. Собственные векторы и собственные значения линейного оператора.

Лине́йный опера́тор — обобщение лин числ функции (точнее, функции  ) на случай более общего множ-ва аргументов и значений. Пусть А – лин-ый оператор из  . Число   наз-ся собственным значением оператора А, если сущ-ет ненул вектор   такой, что А . При этом вектор    наз-ся собственным вектором оператора А, отвечающим собств-ому значению  . Множ-во всех собств-ых значений лин-го оператора А наз-ся его спектром. Для того чтобы число l было собств-ым значением оператора А, необходимо и достаточно, чтобы это число было корнем характеристического ур-ия (7.7) оператора А. Для тождественного оператора все ненул векторы простр-ва являются собственными (с собств-ым значением, равным 1). Для нул оператора все ненул векторы простр-ва являются собств-ыми (с собств-ым значением, равным 0). Наиболее простой вид принимает матрица лин оператора, имеющего n лин-но независимых векторов.

Вопрос №18 Свойства собственных значений и собственных векторов.

Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:1) характеристический многочлен оператора, действующего в Rn является многочленом n -й степени относительно   и не зависит от выбора базиса2) линейный оператор, действующий в Rn имеет не более n различных собственных значений;3) собственные векторы, отвечающие различным собственным значениям, линейно независимы.

Вопрос №20 .Ортогональные матрицы. Диагонализация симметрической матрицы. .

Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на AT равен единичной матрице: Для действительных симметричных матриц собственные векторы действительны и ортонормальны, таким образом, трансформирующая матрица является ортогональной. При этом преобразование подобия является  ортогональным преобразованием: A -> ZTAZ. Хотя действительные несимметричные матрицы и могут быть диагонализированы "почти во всех" случаях, трансформирующая матрица не обязательно будет действительной. Однако выходит так, что "почти" всю работу в этом случае делает также действительное преобразование подобия. Оно может привести матрицу к системе малых блоков (2 x 2), расположенных по диагонали; все остальные элементы будут нулевыми. Каждый из блоков размера (2 x 2) соответствует комплексно - сопряженной паре собственных чисел.

Вопрос №19 Подобные матрицы; их свойства. Задача диагонализации матрицы. Необходимое и достаточное условия приводимости матрицы к диагональному виду. Квадр матр-ы   и   n-го порядка наз-ся подобными, если сущ-ет такая невырожд матр  , что Преобр-ие матр   по формуле   наз-ся преобр-ие подобия, а матрица  — преобраз-ей.Св-ва подобн матриц1. Каждая кв матр подобна самой себе:  .2. Если матр   подобна матр  , то и   подобна   при  .3. Если матр   подобна матр  , а   подобна  , то   подобна  , .4. Подобие явл-ся частным случ эквивалентных преобр-ий.5. В случае ортогональности преобраз-ей матр подобн матр явл-ся конгруэнтными. Если в   сущ-ет базис из собств-х векторов лин опер-ра   то матр лин опер-ра будет диагон-ой в этом базисе Условия сущ-ия.Пусть   – собств-ые значя лин опер-ра   кратностей  , причём  . Если для кажд   сущ-ет   собств-ых векторов – решений ФСР соотв-ей однородной СЛАУ, то сущ-ет базис из собств-ых векторов, а значит, матр   лин опер-ра   можно привести к диагон-му виду. В частности, если  , т. е. спектр лин опер-ра простой, то базис из собств-х векторов сущ-ет.Но, если среди корней характеристического ур-я найдётся хотя бы 1 пара комплексно-сопряжённых, то в веществ-ом лин простр-ве не сущ-ет базиса из собств-ых векторов.Если спектр простой, то матр лин опер-ра в базисе из собств-х векторов будет диагональной.Рассм кв матр  , в столбцах которой стоят координаты собств-х векторов  , соотв-их собств-м знач-ям  . Это ознч-т, что матр   явл-ся матр перехода к базису из собств-х векторов. в этом случае  , т. е. матрица   – невырожд-я, и для неё сущ-ет обратная –  Из опр-я собств-х векторов лин опер-ра следует  Где   – векторы-столбцы, соотв-щие собств-ым векторам   лин опер-ра  .   Где   – диагональная матр, у которой на главн диагонали собств-ые числа   т. е.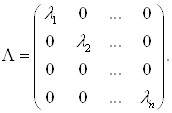 Умножим 2 части рав-ва слева на матрицу  :  или   Это означ, что матр лин опер-ра при переходе к базису из собств-х векторов станет диагональной в результате преобр-ия подобия