
- •Лекционный курс по сапр (система автоматизированного проектирования).
- •Тема 1. Общие сведения о проектировании.
- •Тема 2. Общие сведения о сапр.
- •Техническое обеспечение сапр
- •Математическая модель объектов проектирования.
- •Требования к м.М.
- •Классификация м.М.
- •Постановка задачи теплового расчёта эм методом эквивалентных тепловых схем замещения (пример моделирования на макроуровне).
- •Требования к методам анализа.
- •Методы анализа.
- •Синтез технических объектов сапр.
- •Постановка задачи оптимизации эм.
- •Оптимизация с использованием комплексных агрегированных переменных
- •Программное обеспечение компьютерной графики.
Постановка задачи теплового расчёта эм методом эквивалентных тепловых схем замещения (пример моделирования на макроуровне).
Метод конечных элементов для расчёта температурного поля используется для двухмерной задачи (в плоскости, в поперечном сечении). Для расчёта трёхмерного поля МКЭ возникают трудности, связанные с неоднородной средой, а соответственно с размерами элементов (имеют небольшую толщину по сравнению с размерами проводников и размерами магнитопровода).
При тепловых расчётах объёмных задач в ЭМ большее применение находит метод эквивалентных тепловых схем замещения.
Сущность эквивалентных тепловых схем замещения заключается в том, что ЭМ и охлаждающий воздух разбиваются на элементы. В качестве элементов можно принимать обмотку, либо часть её, полюс, коллектор, зубцовый слой или зубец, элемент станины и т.д.
При этом делаются следующие допущения:
- температура в пределах элемента принимается неизменной
- потери, если они есть в элементе, сосредотачиваются в геометрическом центре элемента
- теплоизлучающим элементом пренебрегаем (тепло передаётся между элементами теплопроводностью и конвекцией).
Если все центры элементов, на которые разбит сектор ЭМ соединить между собой посредством тепловых сопряжений, то получим схему замещения ЭМ подобие электрической схемы. Тепло будет передаваться от более нагретого элемента к менее нагретому.
Для получения математической модели в методе ЭТС замещения воспользуемся уравнением теплового баланса (закон сохранения энергии).
Для однородного тела уравнение теплового баланса записывается следующим образом:
![]() (1)
(1)
![]() -
потери, выделяемые в элементе за время
-
потери, выделяемые в элементе за время
![]()
![]() -эта
составляющая идёт на нагревание элемента
-эта
составляющая идёт на нагревание элемента
![]() -передаётся
охлаждающему воздуху.
-передаётся
охлаждающему воздуху.
![]() -потери
в элементе
-потери
в элементе
-промежуток времени
![]() -удельная
теплоёмкость элемента
-удельная
теплоёмкость элемента
![]() -масса
элемента
-масса
элемента
![]() -превышение
температуры элемента
-превышение
температуры элемента
-коэффициент теплоотдачи с поверхности (обдуваемой)
![]() -величина
обдуваемой поверхности (площадь)
-величина
обдуваемой поверхности (площадь)
-температура (превышение)
Т.к. ЭМ разбита на n-элементов, то вторую составляющую в правой части уравнения (1) можно заменить суммой.
![]() (2)
(2)
Тогда для i-того элемента схемы замещения уравнение (1) можно записать в следующем виде
![]() (3)
(3)
Поделив обе части на получим:
![]()
Если потери в элементе зависят от температуры (для элементов меди потери зависят от температуры а для элементов стали практически не зависят)
![]() -учитывает
потери в стали
-учитывает
потери в стали
![]() (4)
(4)
Разложим уравнение (4) относительно
производной
![]()
![]() (5)
(5)
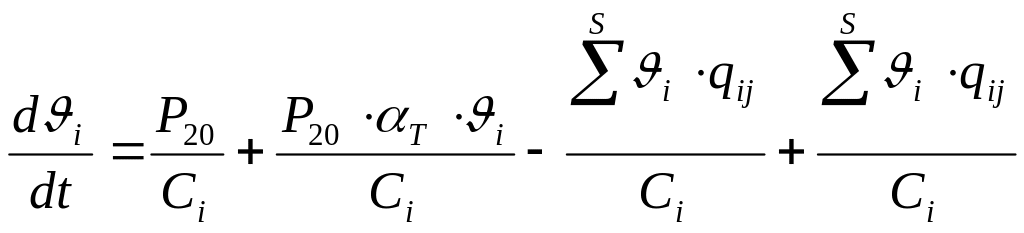
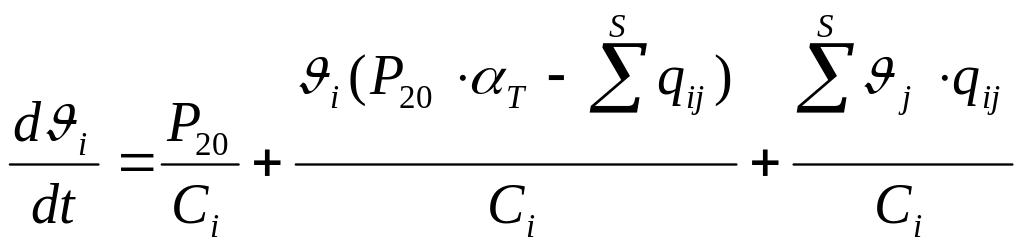
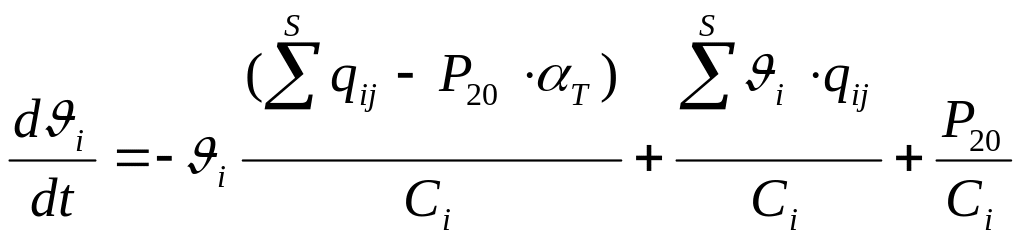
У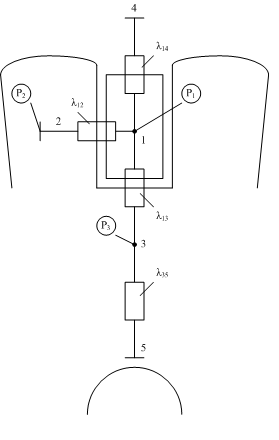 равнение
(6)- это общая запись уравнения теплового
баланса для i-того элемента-
это есть не что иное как обыкновенное
дифференциальное уравнение с постоянными
коэффициентами.
равнение
(6)- это общая запись уравнения теплового
баланса для i-того элемента-
это есть не что иное как обыкновенное
дифференциальное уравнение с постоянными
коэффициентами.
Схема замещения в общем случае описывается для элементов конструкции системой уравнений вида (6).
Уравнение для элементов охлаждающего воздуха представляют собой линейные алгебраические уравнения с коэффициентами, имеющими одностороннюю проводимость.
(Точка 1):
![]()
(Точка 3):
![]()
Анализ и синтез технических объектов САПР.
Анализ - это изучение свойств существующего объекта, а синтез направлен на создание объекта.
Анализ может быть одновариантным и многовариантным.
Анализ технических объектов САПР основан на математическом моделировании, т. е. на исследовании проектируемых объектов путем оперирования их математическими моделями.
Математическое моделирование на микро- и макро-уровнях, как было рассмотрено ранее, описывается системами обыкновенных дифференциальных уравнений или системами линейных и нелинейных алгебраических уравнений. Оперирование такими моделями в одновариантном анализе означает решение соответствующих уравнений, которое возможно, как правило, численными методами.
В многовариантном анализе решения таких систем заключается в многократном повторении при варьировании внутренними и/или внешними параметрами.
Примерами многовариантного анализа является анализ чувствительности и статический анализ.
В математике известно большое число методов решения задач одновариантного, многовариантного анализа, но эффективность их различна. То что приемлемо для решения обычных задач может быть совершенно не эффективно в САПР (решается система из большого числа уравнений, может потребоваться много времени и большой объем оперативной памяти.
