Математическая модель объектов проектирования.

Математическая модель (ММ)-совокупность математических объектов (чисел, символов, множеств и т.д.) и связей между ними, отражающих важнейшие для проектирования свойства проектируемого объекта.

Моделирование большинства технических объектов можно выполнять на микро-, макро- и метоуровнях, эти уровни отличаются степенью детализации рассмотрения процессов в объекте.

М.м. на микроуровне является система дифференциальных уравнений. В частных производных описывающая процессы. В сплошной среде с заданными краевыми условиями.

Но такое решение такой системы удаётся решить лишь для частных случаев, поэтому: 1-я задача при моделировании состоит в построении приближённой дискретной модели. Для этого могут использоваться метод конечных разностей, метод конечных элементов, метод интегральных уравнений 1-м из вариантов которого является метод графических элементов. Система дифференциальных уравнений при испытании этих элементов заменяется системой уравнений.

М.М. на макроуровне описывается системой обыкновенных дифференциальных уравнений с заданными начальными условиями.

М.М. на метоуровне. На метоуровне моделируют в основном 2-е категории технических объектов.

-объекты являются предметом исследования ТАУ

-объекты являются предметом исследования массового обслуживания.

Требования к м.М.

К М.М. предъявляются требования:

-универсальности

-адекватности

-точности

-экономичности.

Степень универсальности М.М. характеризует полноту отображения в модели свойств реального объекта М.М. отображает как правило лишь некоторые свойства объекта, например электромагнитные процессы в электрической машине.

Точность оценивается степенью совпадения значений параметров реального объекта и значений тех параметров рассчитанных с помощью М.М.

Адекватность М.М.- способность отображать заданные свойства объекта с погрешностью не выше заданной.

Экономичность М.М. характеризуется затратами вычислительных ресурсов (время решения задачи, объём оперативной памяти).

Классификация м.М.

По характеру отображаемых свойств М.М. делится на структурные и функциональные.

Структурные предназначены для отображения структурных свойств объекта.

Различают топологические и геометрические М.М. В топологических М.М. отображаются состав и взаимосвязь элементов объекта они могут иметь форму матриц, таблиц и списков.

В геометрической М.М. отображается геометрические свойства объекта в них дополнительно а сведениям о взаимном расположении объектов содержащих сведения о форме детали (они выражаются совокупностями уравнений и алгебраическим соотношением и т.д.).

Функциональные М.М. предназначены для отображения физических и информационных процессов протекающих в объекте. Обычно функциональные М.М. представляют собой системы уравнений связывающие внешние и внутренние выходные параметры. Функциональные М.М. могут описывать электромеханические, механические, гидравлические, оптические, химические и др. процессы функционирования объектов.

М.М. комплексного расчёта магнитных и температурных полей (пример М.М. на микроуровне. Для расчёта температурных полей необходимо знать распределение источников тепловыделений, это в первую очередь относится к областям с ферромагнитными материалами т.к. распределение индукции в магнитопроводе электрической машины то и неравномерно распределены источники тепловыделения (Р_ст).

Потери в элементах магнитопровода состоят из двух составляющих: потери на гистерезисе и от вихревых токов. Для их расчёта необходимо знать индукции отдельных элементов. Для расчёта распределения индукции необходимо рассчитать магнитное поле. Для облегчения расчёта магнитного поля с токонесущими областями используют векторный магнитный потенциал.

Магнитное поле (2^х мерное) в неоднородной нелинейной среде описывается нелинейным дифференциальным уравнением в частных производных.

(1)

Где А и -составляющие векторы магнитного потенциала и плотности тока по оси Z.

-нелинейная величина.

Уравнение (1) получено при следующих допущениях:

-ферромагнитные материалы магнитопровода изотропии и явление гистерезиса не учитываются.

-не учитывается действие вихревых токов.

-заданные токи равномерно распределены по токонесущим областям и изоляцией этих областей, можно пренебречь.

Уравнению (1) могут соответствовать различные граничные условия, можно выделять 3 граничных условий:

1. расчёт магнитного поля при ХХ

2. расчёт магнитного поля в отдельных областях поперечного сечения машины

3. расчет магнитного поля при нагрузке.

В 1^х 2^х типах задач заданы условия Дирихле, т.е. на границах области (отдельных областях) заданы значения векторного потенциала, а на других участках заданы условия Неймана.

(Дирихле)

(Неймана)

В 3^м типе задач, если нагрузки симметричный векторный магнитный потенциал является функцией двойного полюсного деления. Это позволяет выбрать граничные условия так, чтобы рассчитать магнитное поле только на одном полюсном делении (условия периодичности).

В областях с разными средами (воздух-сталь) должны выполнятся следующие условия на границе раздела; т.е. должны быть равны нормальные значения индукции и касательные составляющие напряженности магнитного поля.

B_n и H_t

В методе конечных элементов эти условия выполняются автоматически при получении расчётных уравнений.

В методе конечных элементов (МКЭ) энергетичный функционал, соответствующий уравнению (1) (для 2^х мерного поля) заменяется системой нелинейных алгебраических уравнений.

Для получения расчётной системы нелинейных уравнений расчётная область разбивается на большое количество подобластей (элементов), они могут быть прямоугольные, треугольные и т.д. Наиболее проста система расчётных уравнений получается для треугольных элементов, с их помощью легко апроксимируется сложная граница области.

Для формирования системы расчётных уравнений необходима следующая информация:

1. количество расчётных узлов внутри области

2. количество треугольных элементов

3. массив номеров треугольников и номеров вершин, которые образуют этот треугольник

4. координаты всех узлов области (x,y)

5. массив номеров треугольников с указанием признака среды, где расположен треугольник (воздух или железо).

Постановка задачи расчёта двухмерного температурного поля.

Температурное поле в общем случае в двухмерной области описывается нелинейным дифференциальным уравнением частных производных вида:

(2)

Где , -коэффициенты теплопроводности по осям x и y

-температура (превышение температуры)

-мощность тепловыделений (потери)

Уравнению (2) могут соответствовать 2 вида граничных условий: условие Дирихле, т.е. когда задана температура на границе или условие Коши, т.е.

, -направляющие косинусы внешней нормали к граничной поверхности.

-поток тепла через единичную поверхность.

-превышение температуры охлаждающей среды.

-коэффициент теплоотдачи.

Если ; и , то

Сравнивая уравнения (1) и (2) видим, что они имеют один и тот же вид. Это позволяет использовать 1 алгоритм формирования расчётной системы уравнения.

Рассмотрим расчётную область, в которой будем находить решение поставленной задачи. Область представляет собой сектор машины постоянный ток якоря, приходящийся на половину полюсного деления. Расчёт ведётся без учёта реакции якоря (машина с компенсационной обмоткой и действие реакции якоря незначительное).

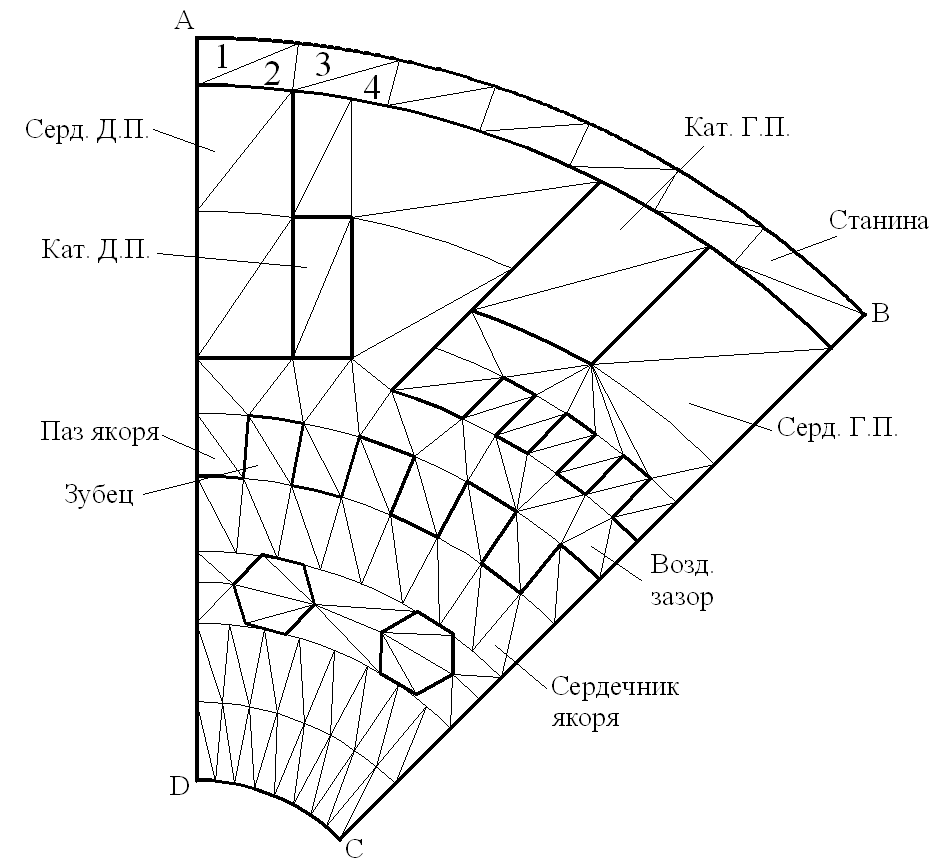
Расчёт магнитного поля производится для всех элементов области (в стали и в воздухе).

Для температурного поля область остаётся той же, но количество узлов и количество треугольников изменяется, исключаются узлы и треугольники, легко делящиеся в воздухе.

В тепловой задаче граничные условия выглядят следующим образом AD, DC, BC , а на всех остальных границах, омываемых воздухом выполняется условие Коши.