2. Введение обратной связи.

Определение. Выходная переменная зависит от входной переменной с запаздыванием, если для любого момента времени и для любых входных последовательностей

Если автоматная функция задана каноническими уравнениями, то в уравнении переменная будет отсутствовать, так как для она является фиктивной.

Если переменная зависит от входной переменной с запаздыванием, можно ввести обратную связь по переменным .

На рис. 22 схематично показано введение обратной, если автоматная функция реализована СФЭЗ. На схеме видно, что при такой процедуре уменьшается и число входных переменных, и выходных переменных, может уменьшиться вес функции.

Рис. 22

Если автоматная функция задана каноническими уравнениями, то во всех уравнениях вместо переменной надо поставить функцию .

Пример 11. Построить канонические уравнения автоматной функции, если в системе канонических уравнений:

ввести обратную связь по переменным .

зависит с запаздыванием, так как не входит в уравнение для . Подставив его вместо , получим

Уравнение можно упростить и привести систему к тривиальному виду

или

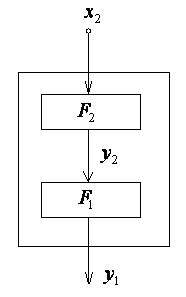
3. Суперпозиция двух автоматных функций

Если функция реализована СФЭЗ, то схематично она изображена на рис.23

Рис. 23

Один или несколько выходов функции поступают на входы , может иметь и свои входные переменные. Если функция имела вес , функция имела вес , то вес суперпозиции не превосходит .

Мы ограничимся автоматными функциями с одним входом и причем у функции входная переменная выходная , выходная для имеет вид:

Если и заданы каноническими уравнениями, то вместо в систему для подставим , и добавим к системе уравнений уравнения задающие состояния автомата , вместе с начальными условиями.

Пример 12. Автоматные функции и заданы каноническими уравнениями:

Построить канонические уравнения автоматной функции и найти ее вес.

Так как у нас осталось только одна входная переменная, положим , аналогично: и упростим систему уравнений.

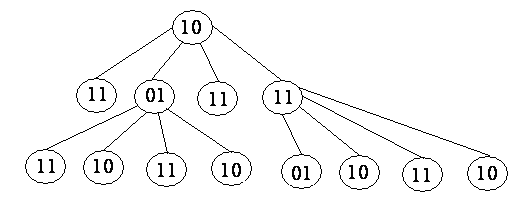
Построим информативное дерево, состояние в корне дерева (01)

Рис. 24

Эквивалентных состояний нет, поэтому вес дерева равен 4.

Рассмотрим еще один пример, который не связан с действиями с автоматными функциями.

Пример 13. Реализовать схемой из функциональных элементов с задержкой минимальной сложности в стандартном базисе, где суперпозицию функций по переменным

Канонические уравнения для суперпозиции по указанным переменным получаются подстановкой выражения для вместо переменной в канонические уравнения для и добавляем к полученной системе уравнения и начального условия .

Перейдем к стандартному базису, по возможности, уменьшая сложность:

Вес полученной суперпозиции не превосходит четырех, но может быть и меньше. Для определения веса построим информативное дерево.

Душ, выходящие из каждой вершины, соответствуют наборам : (00), (01), (10), (11).

Рис.25

Вес функции равен трем, так как в дереве нет эквивалентных состояний, а состояние 00 отсутствует. Для описания трех состояний переменные и необходимы и упростить систему дальше не удается. Постоим СФЭЗ.

Рис.26

25