§3. Схемы из функциональных элементов с задержкой с одним входом и одним выходом

Рассмотрим автоматную функцию, задерживающую информацию на 1 шаг по времени, т.е.

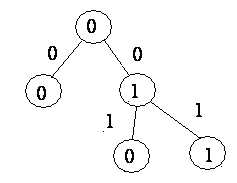
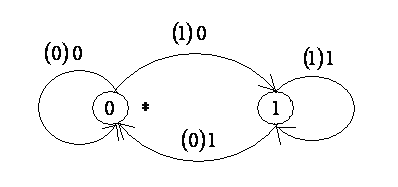
Построим для нее усеченное дерево, диаграмму Мура и канонические уравнения.

Рис.17

Канонические уравнения:

Такой автомат с единичной задержкой называется элементом задержки.

Определение. Схемой из функциональных элементов с задержкой – СФЭЗ в некотором базисе состоящем из функций алгебры логики и элементов задержки называется орграф, удовлетворяющий следующим требованиям:

1. любой вершине графа приписана переменная, разным вершинам приписаны разные переменные;

2. любой вершине, куда входит дуг, сопоставлен элемент из базиса, зависящий от переменных, взаимно–однозначным образом соответствующих дугам;

3. выделено некоторое количество вершин, названных выходными;

4. в графе есть орциклы, но каждый ориентированный цикл проходит через элемент задержки.

Это последнее условие отличает СФЭЗ от СФЭ.

Рассмотрим функционирование СФЭЗ. Пусть в схеме есть элементов задержки . Рассмотрим орцикл, проходящий через элемент задержки .

Пусть вершины графа, в вершину помещен элемент задержки , вершине приписана переменная , вершине – переменная .

Пусть входным вершинам приписаны переменные , выходным вершинам приписаны переменные .

Удалим из графа дуги и элементы задержки, тем самым мы ликвидируем орциклы. Вершины отнесем к входным, так как в них не входит ни одна дуга, а вершины – к выходным. Получим СФЭ с входными переменными и выходными переменными , .

В каждой выходной вершине реализуется некоторая функция от входных переменных

,

.

Так происходит в каждый момент времени, следовательно, для любого момента времени

,

.

Теперь вернемся к элементам задержки: и получим систему уравнений

,

.

Эти уравнен6ия являются каноническими для СФЭЗ и описывают ее функционирование.

Канонические уравнения для СФЭЗ с элементами задержки совпадают с каноническими уравнениями автоматной функции веса . Поэтому для любой автоматной функции можно построить СФЭЗ, которая будет ее реализовывать.

Пример 9. Построить СФЭЗ в базисе , с входами , осуществляющую сложение двух входных последовательностей (пример 2).

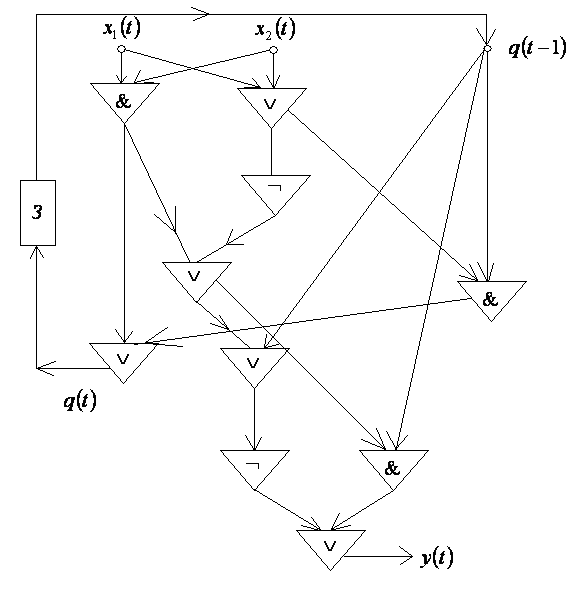
Канонические уравнения для этой функции получены (пример 4). Упростим их, чтобы получить схему как можно меньшей сложности.

.

Переменные сделаем входными, переменные и – выходными, построим СФЭ.

Рис. 18

Затем выходную переменную через элемент задержки отождествляем с .

§ 4. Операции над автоматными функциями

Рассмотрим некоторые операции над автоматными функциями.

1. Отождествление двух или большего числа входных переменных. Если функция реализована схемой, то соответствующие этим переменам вершины будут просто отождествлены.

Если функция задана каноническими уравнениями, то при отождествлении каких-то переменных может уменьшиться вес автоматной функции.

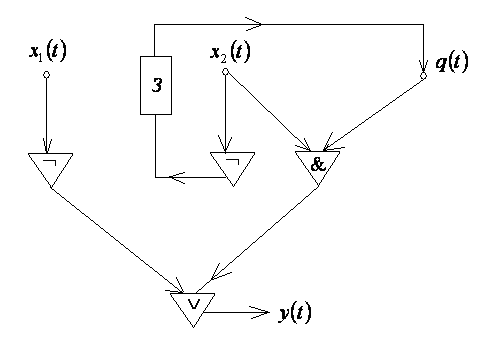
Пример 10. Реализовать СФЭЗ автоматную функцию, получающуюся из заданной:

отождествленными переменных и .

Положив , получим систему уравнений

Для определения веса этой функции надо построить дерево по системе канонических уравнений, вершины будем нумеровать двоичными кодами: .

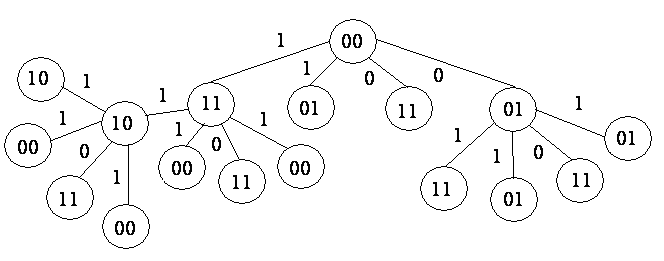
Рис. 19

Когда строим дерево по заданной системе канонических уравнений, мы сразу получаем усеченное дерево. На графе видно, что состояние , а состояние . Поэтому вес функции равен 2, можно получить более простую систему уравнений и, следовательно, более простую СФЭЗ для ее реализации. Начальное состояние обозначим 0, другое 1, построим информативное дерево:

Рис. 20

и каноническую таблицу

0	0	0	1	1
0	0	1	1	1
0	1	0	1	0
0	1	1	1	0
1	0	0	0	1
1	0	1	0	1
1	1	0	0	0
1	1	1	1	0

По канонической таблице получим простую систему уравнений:

и СФЭЗ для нее реализации

Рис. 21