34. Сопряженные, самосопряженные и унитарные операторы и их свойства

Совокупность всех непрерывных линейных функционалов, определенных на некотором линейном нормированном пространстве Е, образует линейное пространство, которое называется пространством, сопряженным с Е, и обозначается .

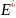Рассмотрим непрерывный линейный оператор у=Ах, отображающий линейное топологическое пространство Е в такое же пространство . Пусть – линейный функционал, определенный на , т.е. . (g, Ax)=( ).

Это соотношение можно принять за определение сопряженного оператора.

Линейный оператор А, действующий в евклидовом пространстве, называют самосопряженным если

Линейный оператор самосопряженный, если для любых векторов х и у верно равенство

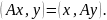
Определение: пусть H – комплексное гильбертово пространство. Линейный оператор U называется унитарным, если он отображает пространство H на все H с сохранением нормы, т.е. если U :H →H и = .

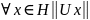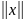Замечание: свойства унитарных операторов таковы: унитарные операторы действительно являются линейными операторами, кроме того, любой унитарный оператор ограничен, имеет обратный оператор, который также унитарен.

Теорема (критерий унитарного оператора): пусть H – комплексное гильбертово пространство. Линейный ограниченный оператор U :H→H является унитарным тогда и только тогда, когда

31. Компактность операторов. Критерий компактности в пространстве Теорема Рисса (с доказательством).

Оператор , отображающий банахово пространство в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если он каждое ограниченное множество переводит в предкомпактное.

Для компактности множества в полном метрическом пространстве необходимо и достаточно, чтобы оно было замкнутым и вполне ограниченным.

32. Компактные операторы. Теорема Арцелла. (док-во достаточности).

Оператор , отображающий банахово пространство в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если он каждое ограниченное множество переводит в предкомпактное.

Теорема Арцелла: Для того, чтобы Семейство оператора A определённых на некотором отрезке [a,b] было компактным, необходимо и достаточно, чтобы этот оператор был равномерно ограниченным и равностепенно непрерывным.

Достаточность[править исходный текст]

Необходимо доказать, что равномерная ограниченность и равностепенная непрерывность семейства F влечёт существование конечной -сети для всякого конечного .Фиксируем .

Пусть K — это константа, которая фигурирует в определении равномерной ограниченности.

Выберем такое 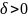, которое фигурирует в определении равномерной непрерывности и соответствует величине 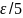. Рассмотрим прямоугольник 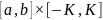и разобьём его вертикальными и горизонтальными прямыми на прямоугольные ячейки размером меньше чем 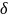по горизонтали и по вертикали. Пусть ,…, — узлы этой решётки (по оси абсцисс).

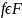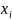Если рассмотреть произвольную функцию , то для каждого узла решётки обязательно найдётся такая точка решётки, что . Если рассмотреть ломаную функцию , которая в узлах принимает соответствующие значения, уклоняющиеся от функции не более чем на , то в силу того что сама функция уклоняется на каждом отрезке не более чем на , ломаная на каждом таком отрезке уклоняется не более чем на .

Поскольку каждая точка x отрезка [a,b] оказывается на одном из таких отрезков, скажем, [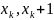 ], то получается что уклонение функции от построенной таким образом ломанной не превосходит :

.

Тем самым показано, что конечная (!) система ломанных функций указанного вида является -сетью для заданного .