21. Сопряженное пространство. Теорема о полноте сопряженного пространства

22. Гильбертово пространство. Неравенство Коши-Буняковского

23. Компактные операторы. Свойства. Примеры.

24. Линейные операторы в линейных нормированных пространствах

25. Теорема Хана-Банаха о продолжении линейного функционала (с док-вом). Следствия.

26. Принцип сжимающих отображений (с док-ом) и его применение.

27. Интегральные уравнения Вольтерра второго рода. Представление решения через резольвенту ядра.

28. Спектр оператора в Банаховом пространстве. Резольвента. Аналитические свойства резольвенты.

29. Собственные значения интегрального уравнения с вырожденным ядром. Методика нахождения собственных значений интегрального уравнения с вырожденным ядром.

30. Ортогональные и ортонормальные системы в Гильбертовых пространствах. Пример ортогональной системы.

31. Компактность операторов. Критерий компактности в пространстве Теорема Рисса (с доказательством).

32. Компактные операторы. Теорема Арцелла. (док-во достаточности).

33. Пространства со скалярным произведением. Гильбертовы пространства. Примеры гильбертовых пространств.

34. Сопряженные, самосопряженные и унитарные операторы и их свойства.

35. Ряд Фурье по тригонометрической системе на симметричных отрезках

36. Сопряженные, самосопряженные и унитарные операторы в Гильбертовых пространствах.

37. Интегральные уравнения с вырожденным ядром. Методика решения интегральных уравнений с вырожденным ядром.

38. Интегральные уравнения Фредгольма. Случай вырожденных ядер.

39. Операторы с чисто точечным спектром. Теорема о связи с собственными значениями (с док-ом).

40. Слабая компактность шара в сопряженном пространстве. Теорема о вложенных шарах (с док-ом).

21. Сопряженное пространство. Теорема о полноте сопряженного пространства

Пусть L - линейное пространство над полем P .

Линейным функционалом на пространстве L называется отображение , обладающее свойством: , где

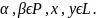
Обозначим через 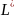множество всех линейных функционалов на L.

Определим операции сложения и умножения на числа по формулам:

1)

2)

Таким образом, на множестве вводится структура линейного пространства. Это линейное пространство называется сопряженным пространством для пространства L .

Теорема о полноте сопряженного пространства

22. Гильбертово пространство. Неравенство Коши-Буняковского.

Гильбертово пространство - линейное (векторное) пространство (над полем вещественных или комплексных чисел), в котором для любых двух элементов пространства x и y определено скалярное произведение (x,y) и полное относительно порожденной скалярным произведением метрики . Если условие полноты пространства не выполнено, то говорят о предгильбертовом пространстве. Гильбертово пространство есть банахово пространство (полное нормированное пространство).

23. Компактные операторы. Свойства. Примеры.

Определение: Оператор , отображающий банахово пространство в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если он каждое ограниченное множество переводит в предкомпактное.

Свойства компактных операторов

1. Любой линейный компактной оператор является ограниченным, следовательно, непрерывным.

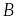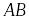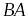2. Если – компактный оператор, – ограниченный, то операторы и – компактные.

3. Если операторы и компактные, действующие из нормированного пространства 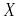в нормированное пространство 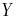и 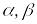– любые числа, то оператор 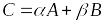также компактен.

4. Если 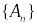– последовательность компактных операторов в банаховом пространстве , сходящаяся по норме к некоторому оператору , то оператор тоже компактен.

5. Оператор, сопряженный компактному оператору, компактен.

Примеры компактных операторов.

1. Одномерный линейный оператор вида: 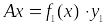, где – фиксированный элемент из пространств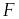а , а 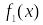– фиксированный линейный функционал из пространства , которое является банаховым пространством.

2. В пространстве непрерывных функций важный класс компактных операторов образуют операторы вида:

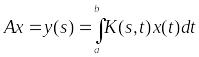(3), где функция непрерывна на квадрате .

24. Линейные операторы в линейных нормированных пространствах

Непустое множество элементов называется линейным, если оно удовлетворяет таким условиям:

I. Для любых двух элементов определен единственный элемент , называемый суммой и обозначаемый , причем

1) ; 2) ; 3) в существует такой элемент 0, что для всех ; 4) для каждого существует такой элемент , что .

II. Для любого числа и любого элемента определен элемент , причем

1) ; 2) ; 3) ;

4) ;

Множество называется нормированным пространством, если:

1) – линейное пространство над полем действительных или комплексных чисел.

2) Для каждого элемента определено вещественное число, называемое его нормой и обозначаемое , и выполнены условия:

а) для любого ;

б) для любого и любого ;

в) , для любых

Пусть – линейные нормированные пространства.

Линейным оператором, действующим из в , называется отображение , удовлетворяющее условию: для любых , .

Будем говорить, что в (вещественной или комплексной линейной системе) определен функционал , если каждому элементу поставлено в соответствие некоторое вещественное (комплексное) число .

Линейный оператор, действующий из Е в Е₁, называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное.

Оператор А называется непрерывным в точке , если для любой последовательности выполняется условие .

Оператор А называется непрерывным, если он непрерывен в каждой точке пространства Е.

Теорема: Для того, чтобы линейный оператор был непрерывным, необходимо и достаточно, чтобы он был ограничен.