Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Уфимский Государственный Авиационный Технический Университет»

в г. Кумертау

Кафедра ЕН и ОТД

Лабораторная работа № 4 Определение моментов инерции твердых тел методом трифилярного подвеса

Заведующий кафедрой ЕН и ОТД:

профессор Даутов А.И.

Составил: Старший преподаватель

Медведев И.А.

Кумертау 2010г.

Определение моментов инерции твердых тел методом трифилярного подвеса

Приборы и принадлежности: 1. Трифилярный подвес;

2. Набор твердых тел, подлежащих измерению

(диск, стержень, полый цилиндр);

3. Секундомер;

4. Штангенциркуль;

5. Масштабная линейка.

Цель работы:

1.Эксперементальное определение моментов инерции твердых тел.

2. Проверка теоремы Штейнера.

Теория метода

Момент инерции твердого тела относительно некоторой оси определяется выражением

J=∑∆miri²; J=∫r²dm; (1) где ri расстояние элемента массы от оси ∆mi вращения.

1. Момент инерции J является мерой инертности при вращательном движении. Величина момента инерции зависит от массы данного тела и от ее распределения относительно оси вращения.

2. Момент инерции некоторых однородных тел правильной геометрической формы можно найти теоретически. Возьмем, например, однородный сплошной цилиндр. Это тело, можно мысленно разбить на тонкие цилиндрические слои, частицы которых находятся на одинаковом расстоянии от оси. Цилиндр радиуса разобьем на концентрические слои толщиной dR (рис.1)

Рис 1.

Пусть радиус какого-то слоя R , тогда масса частиц, заключенных в этом слое будет:

dm=2ΠRhpdR, (2)

Где h – высота цилиндра;

p – плотность вещества цилиндра.

Все частицы слоя будут находиться на расстоянии R от оси, следовательно, момент инерции этого слоя будет:

DJ=dmR²=2ΠphR³dR; (3)

Тогда момент инерции всего цилиндра:

J=∫dJ=∫R²dm=2Πhp∫R³dR=2Πph(R/4) (4)

Поскольку масса цилиндра m=ΠR²ph, формула (4) запишется так:

J_с=1/2mR²_цил.; (5)

Момент инерции полого цилиндра, имеющего внутренний радиус R, а внешний – R. Просто вычислить по формуле (4), интегрируя в пределе от R до R :

J=2Πph∫R³dR=2Πph(R /4- R /4); (6)

Так как масса полого цилиндра m=Πph(R²- R²), его момент инерции можно записать так:

J_с=1/2m(R²+ R²); (7)

Таким же простым методом можно вычислить момент инерции любого тела, которое можно разбить на: совокупность колец, дисков: и т.д. Момент инерции неоднородных тел и тел произвольной формы определяется опытным путем. Например: при помощи трифилярного подвеса, как в данной работе. Если каким-то способом определить момент инерции тела относительно некоторой оси, проходящей через центр массы, то очень просто определить момент инерции тела относительно любой параллельной оси. Момент инерции зависит и от направления оси и от места её прохождения. Если нет специальной оговорки, то предполагается, что ось вращения проходит через центр инерции тела. Если ось сдвинута по отношению к центру инерции (рис. 2) на расстояние d, то новый момент инерции J, будет отличен от момента инерции J относительно параллельной оси ССт, проходящей через центр инерции.

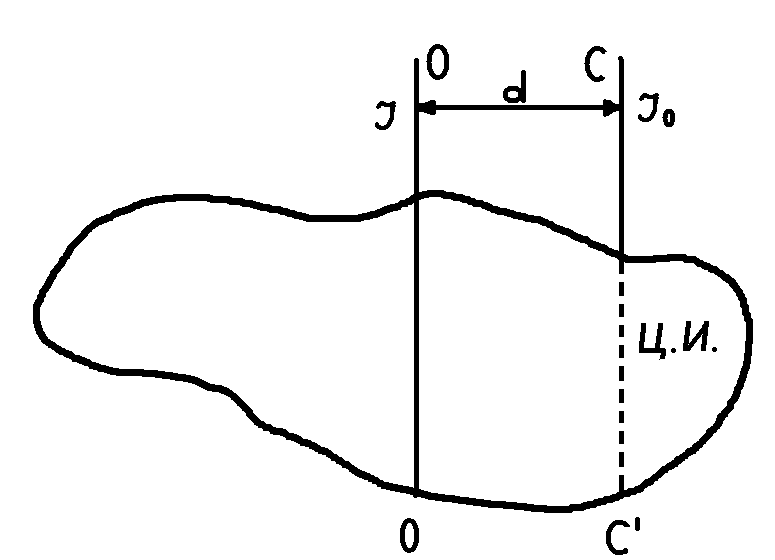
J= J_с +md²; (8)

Данное выражение представляет собой теорему Штейнера, которая формулируется так:

Момент инерции тела относительно оси, не проходящей через центр инерции равен моменту инерции этого тела относительно параллельной ей оси, проходящей через центр инерции, плюс произведение массы тела, на квадрат расстояния от оси до центра инерции.

Кинетическая энергия тела при вращении около неподвижной оси равна:

Wкин= Jω²/2; (9)