7. Геометрическое и аналитическое условие равновесия сходящейся системы сил. Теорема о трех силах.

1.Геометрическое условие равновесия. Так как равнодействующая R сходящихся сил определяется как замыкающаяся сторона силового многоугольника, построенного из этих сил, то Rможет обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой, т.е. когда многоугольник замкнётся. Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугльник, постоенный из этих сил, был замкнут. 2.Аналитические условия равновесия. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трёх координатных осей были равны нулю. Теорема о трёх силах. Если свободное твёрдое тело находится в равновесии под действием трёх непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Доказанная теорема выражает необходимое, но недостаточное условие равновесия свободного твёрдого тела под действием трёх сил.

8. Алгебраический момент силы относительно центра и его свойства.

Вращательный эффект силы характеризуется ее моментом. Моментом силы F относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча. . Отметим следующие свойства момента силы: 1.Момент силы не изменяется при переносе точкиприложения силы вдоль её линии действия. 2.Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю). 3. Момент силы численно выражается удвоенной площадью треугольника ОАВ.

9. Понятие о ферме, назначение, применение. Простейшая ферма. Зависимость между количеством шарниров и стержней. Основные определения и допущения.

Фермой называется жёсткая конструкция из прямолинейных стержней, соединённых на концах шарнирами. Если все стержни лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие.

10. Определения усилий в стержнях фермы методом вырезания узлов. Достоинства и недостатки метода.

Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом

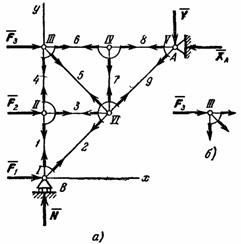из узлов фермы. Ход расчётов поясним на конкретном примере. Рассмотрим изображённую на рис,83 ферму, образованную из одинаковых равнобедренных прямоугольных треугольников, действующих на силы параллельны оси x и равны : F1=F2=F3=F=2T. В этой ферме число узлов n=6, а число стержней k=9. Следовательно соотношение выполняется и ферма является жёсткой, без лишних стержней. Составляя уравнения равновесия для фермы в целом, найдём, что реакции опор направлены, как показано на рисунке, и численно равны Переходим к определению усилий в стержнях. Пронумеруем узлы фермы римскими цифрами, а стержни арабскими. Искомые усилия будем обозначать (в стержне 1)…Отрежем мысленно все узлы вместе со сходящимися в нихстержнями от осталтьной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям … Изображаем сразу эти силы на рисунке, напрвляя их от узлов, т.е. считая все стержни растянутыми. Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия , . Начинаем с узла 1, где сходятся 2 стержня, так как из 2 уравнений равновесия можно определить только 2 неизвестных усилия. Составляя уравнения равновесия для узла 1, получим , . Отсюда находим , Теперь ,зная S1, переходим к узлу 2. Для него уравнения равновесия дают S3+F2=0, S4-S1=0,откуда S3=-F=-2T, S4=S1=-1T. Определив S4, составляем аналогичным путём уравнения раывновесия сначала узла 33, а затем узла 4. Из этих уравнений находим: , , . Для вычисления S9 составляем уравнени равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим , откуда . Второе уравнение равновесия для узла 5 и два уравнения для узла 4 можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уранения равновесия всей фермы в целом при определении . Окончательные результаты можно занести в таблицу:

№ стержня…….	1	2	3	4	5	6	7	8	9
Усилие в Т……..	-1	-2,82	-2	-1	+1,41	-3	0	-3	-4,23

Как показывают знаки усилий , стержень 5 растянут, остальные сжаты, стержень 7 не нагружен (нулевой стержень). Наличие в ферме нулевых стержней обнаруживается сразу, так как если в узле, не нагруженном внешними силами, сходятся 3 стержзня, из которых 2 направлены вдоль одной прямой, то усилие в третьем стержне равно нулю.