3. Оценка качества всего уравнения регрессии

В таблице № 3 приведены вычисленные (предсказанные) по модели значения зависимой переменной У и значения остаточной компоненты. Значение коэффициентов детерминации и множественной корреляции можно найти по таблице Регрессионная статистика.

Коэффициент множественной корреляции:

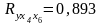
Он показывает, что связь между переменной У и объясняющими переменными х2 и х3 является сильной.

Коэффициент детерминации:

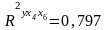
Он показывает долю вариации результативного признака под воздействием изучаемых факторов. В нашем случае 79,7 % вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов х2 и х3.

4. Проверка значимости уравнения регрессии на основе вычисления f-критерия Фишера.

Значение F-критерия Фишера можно найти в таблице № 3 протокола EXCEL, а имеено F_факт=43,23.

Для определения табличного значения F-критерия при доверительной вероятности 0,95 и пр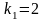и и 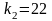воспользуемся функцией FРАСПОБР.

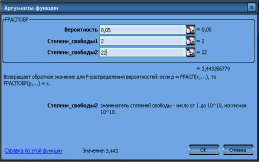
В результате получаем значение F-критерия, равное 3,44. Поскольку F_факт > F_табл, то уравнение регрессии с вероятностью 0,95 следует признать статистически значимым.

5.Оценка статистической значимости коэффициентов уравнения множественной регрессии с помощью t-критерия Стьюдента

Значимость коэффициентов уравнения регрессии, оценим с использованием t-критерия Стьюдента.

Расчетные значения t-критерия Стьюдента для коэффициентов уравнения регрессии, приведены в таблице № 3 протокола EXCEL.

t_расч1‌ ‌= 7,832

t_расч2‌ ‌= -0,107

Табличное значение t-критерия Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР.

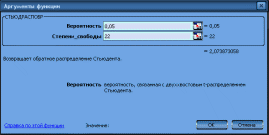
Табличное значение t-критерия Стьюдента при пятипроцентном уровне значимости и степенях свободы (25-2-1) составляет 2,07388. Так как для х2 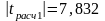_> t _табл, то коэффициент регрессии а2 при x2 с вероятность 95% является статистически значим. Для х₃ 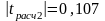< t _табл, следовательно коэффициент регрессии а3 при x3 статистически незначим и фактор х3 не значим.

6. Анализ влияния факторов на зависимую переменную по модели (для каждого коэффициента регрессии вычислить коэффициент эластичности, β-коэффициент)

Учитывая, что коэффициент регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, расчитаем коэффициенты эластичности (Э) и бета-коэффициенты, по следующим формулам:

;

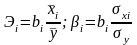Используя математические и статистические функции, найдем средние значения переменных и средние квадратические отклонения.

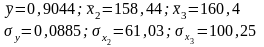
Рассчитаем коэффициенты эластичности. Коэффициент эластичности показывает, на сколько процентов в среднем изменится зависимая переменная, если фактор изменится на 1%.

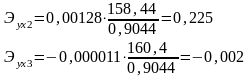Таким образом, при увеличении только фактического потребления домашних хозяйств на 1% индекс человеческого развития увеличится в среднем на 0,225%, а при увеличении только индекса потребительских цен на 1% индекс человеческого развития снизится в среднем на 0,002%.

Рассчитаем бета-коэффициенты. Бета-коэффициент с математической точки зрения показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.

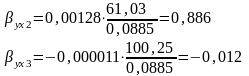
Таким образом, бета-коэффициенты показывают, что, так как коэффициент β_ух2>β_ух3, то второй фактор оказывает на индекс человеческого развития большее влияние, чем третий.