Решение задачи:
1. Построение системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции. Выбор факторных признаков для построения двухфакторной регрессионной модели.
Статистические данные по всем переменным приведены в табл. 1. Из условия следует, что n=25, m= 3.
Для построения корреляционного анализа воспользуемся пакетом прикладных программ Microsoft Excel, функцией «Анализ данных».
Выполняем следующие действия:
Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.
Выбрать команду «Сервис» → «Анализ данных».
В диалоговом окне «Анализ данных» выбрать инструмент «Корреляция», а затем щелкнуть кнопку «ОК».
В диалоговом окне «Корреляция» в поле «Входной интервал» необходимо ввести диапазон ячеек, содержащих исходные данные. Если введены и заголовки столбцов, то установить флажок «Метки в первой строке».
Выбрать параметры вывода. В данном случае «Новый рабочий лист».
«ОК»
Таблица 2
Результаты корреляционного анализа
|
y |
x1 |
x2 |
x3 |
y |
1 |
|
|
|
x1 |
0,874796 |
1 |
|
|
x2 |
0,892779 |
0,932276 |
1 |
|
x3 |
-0,48126 |
-0,51986 |
-0,5293 |
1 |
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная Y, т.е. индекс человеческого развития, имеет тесную связь с ВВП на душу населения по итогам 2009 г. (ryx1 = 0,875) и с фактическим конечным потреблением домашних хозяйств по паритету покупательной способности на душу населения (ryx2 = 0,893). С индексом потребительских цен зависимая переменная Y имеет слабую обратную связь (ryx3=-0,481). Между объясняющими факторами х1 и х2 наблюдается тесная взаимосвязь, что говорит о том, что они являются дублирующими, то есть мультиколлинеарными. Из них выберем тот, который оказывает наибольшее влияние на зависимую переменную у (фактор х2). Таким образом в модели остаются факторы х1 и х3.
2.Рассчитаем параметры линейной модели регрессии
Для того чтобы составить уравнение регрессии зависимости индекса человеческого развития от ожидаемой продолжительности жизни при рождении 2009г. и суточной калорийности питания населения, воспользуемся функцией программы Microsoft Excel, а именно инструмента «Регрессия».
Применение инструмента «Регрессия»
(Анализ данных EXCEL)
Для проведения регрессионного анализа необходимо выполнить следующие действия:
Выбрать команду «Сервис»→ «Анализ данных».
В диалоговом окне «Анализ данных» выбрать инструмент «Регрессия», а затем щёлкнуть по кнопке ОК.
В диалоговом окне «Регрессия» в поле «Входной интервал У» ввести адрес одного диапазона ячеек, который представляет зависимую переменную. В поле «Входной интервал Х» ввести адреса одного или нескольких диапазонов, которые содержат значения независимых переменных.
Если введены и заголовки столбцов, то следует установить флажок «Метки в первой строке».
Выбрать параметры вывода. В данном случае «Новая рабочая книга».
ОК
Результат произведенных действий см. Таблицу 3
Таблица 3
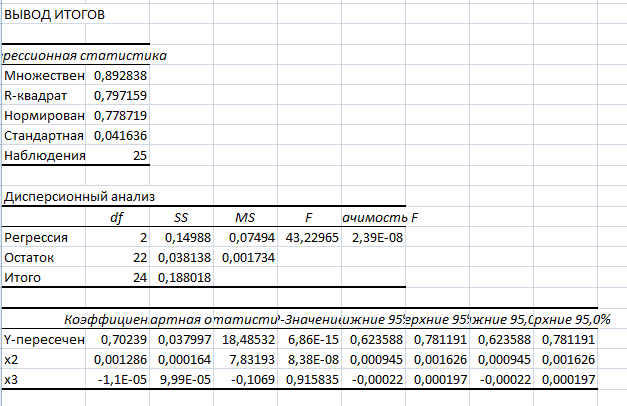
Для того чтобы составить уравнение регрессии по нашим данным, проанализируем полученные итоги. Найдем графу «Коэффициенты» в Таблице 3.
У= 0,7024 +0,0013х2-0,000011х3
Вывод: при увеличении фактического потребления домашних хозяйств на 1 при той же величине индекса потребительских цен индекс человеческого развития увеличится в среднем на 0,0013. А при увеличении индекса потребительских цен на 1% при той же величине фактического потребления домашних хозяйств индекс человеческого развития снизится в среднем на 0,000011.