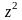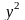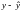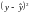Построение гиперболической модели парной регрессии.
Уравнение
гиперболической регрессии:
.
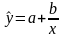Произведем
линеаризацию модели путем замены
.
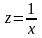В результате получим линейное уравнение
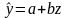
Рассчитаем его параметры по данным следующей рабочей таблицы.
№ |
х |
у |
Z |
yz |
|
|
|
|
|
|
1 |
10 |
26 |
0,100 |
2,600 |
0,01 |
676 |
9,583 |
16,417 |
269,53 |
0,63 |
2 |
71 |
30 |
0,014 |
0,423 |
0,00020 |
900 |
30,028 |
-0,028 |
0,00 |
0,00 |
3 |
17 |
11 |
0,059 |
0,647 |
0,00346 |
121 |
19,381 |
-8,381 |
70,25 |
0,76 |
4 |
64 |
26 |
0,016 |
0,406 |
0,00024 |
676 |
29,662 |
-3,662 |
13,41 |
0,14 |
5 |
22 |
6 |
0,045 |
0,273 |
0,00207 |
36 |
22,563 |
-16,563 |
274,33 |
2,76 |
6 |
13 |
10 |
0,077 |
0,769 |
0,00592 |
100 |
15,074 |
-5,074 |
25,75 |
0,51 |
7 |
11 |
9 |
0,091 |
0,818 |
0,00826 |
81 |
11,746 |
-2,746 |
7,54 |
0,31 |
8 |
61 |
31 |
0,016 |
0,508 |
0,00027 |
961 |
29,479 |
1,521 |
2,31 |
0,05 |
9 |
83 |
44 |
0,012 |
0,530 |
0,00015 |
1936 |
30,513 |
13,487 |
181,91 |
0,31 |
10 |
44 |
33 |
0,023 |
0,750 |
0,00052 |
1089 |
27,971 |
5,029 |
25,29 |
0,15 |
∑ |
396 |
226 |
0,453 |
7,724 |
0,031 |
6576 |
|
7,11E-15 |
870,315 |
5,616 |
Уравнение регрессии имеет вид:
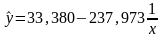
Определим индекс корреляции
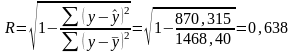
Связь между показателем у и фактором х можно считать умереной, так как 0,5<R<0,7
Индекс
детерминации: детерминации
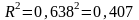
Вариация результативного признака у (объем выпуска продукции) на 40,7% объясняется вариацией фактора х (объем капиталовложений). На остальные факторы, не учтенные в модели, приходится 59,3%.
Рассчитаем F-критерий Фишера:
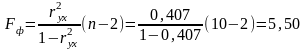
для α=0,05; k1=m=1, k2=n-m-1=8.
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, так как
Средняя относительная ошибка:
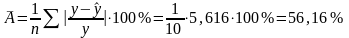
В среднем расчетные значения для гиперболической модели отличаются от фактических значений у на 56,16%, что выходит за пределы нормы.
9) Выбор лучшей модели.
Для выбора лучшей модели построим сводную таблицу результатов.
-
Коэффициент детерминации R
F-критерий Фишера
Коэффициент (индекс) корреляции
Относительная ошибка
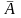
Линейная
0,666
15,97
0,816
39,00%
Степенная
0,610
12,51
0,781
35,75%
Гиперболическая
0,407
5,50
0,638
56,16%
Все модели имеют примерно равные характеристики, но большее значение F-критерия Фишера и большее значение коэффициента детерминации имеет линейная модель. Ее можно взять для построения прогноза.
10) Прогнозироание.
Xmax=83, следовательно, xp=83∙0,8=64,4
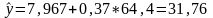
Рассчитаем доверительный интервал прогноза
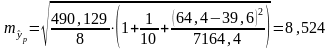
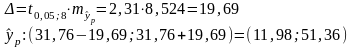
Определим
точность прогноза:
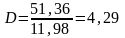
Выполненный прогноз оказался не надежным (р=1-α=1-0,05=0,95), и не точным, так как диапазон верхней и нижней границ составляет 4,29.