
- •Задача 1.
- •Решение
- •5. Проверим предпосылки мнк.
- •Построение степенной модели парной регрессии.
- •Построение гиперболической модели парной регрессии.
- •9) Выбор лучшей модели.
- •Задача 2.
- •Решение задачи:
- •1. Построение системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции. Выбор факторных признаков для построения двухфакторной регрессионной модели.
- •Результаты корреляционного анализа
- •2.Рассчитаем параметры линейной модели регрессии
- •3. Оценка качества всего уравнения регрессии
- •4. Проверка значимости уравнения регрессии на основе вычисления f-критерия Фишера.
- •5.Оценка статистической значимости коэффициентов уравнения множественной регрессии с помощью t-критерия Стьюдента
- •6. Анализ влияния факторов на зависимую переменную по модели (для каждого коэффициента регрессии вычислить коэффициент эластичности, β-коэффициент)
5. Проверим предпосылки мнк.
а) Проверка равенства математического ожидания остаточной последовательности нулю.
Вычислим среднее значение ряда остатков.
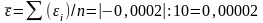 .
.
Так
как
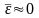 ,
то модель не содержит постоянной
систематической ошибки и адекватна по
критерию нулевого среднего.
,
то модель не содержит постоянной
систематической ошибки и адекватна по
критерию нулевого среднего.
б) Проверка свойства гомоскедастичности
Расположим
значения факторного признака
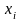 в порядке возрастания.
в порядке возрастания.
х |
10 |
11 |
13 |
17 |
22 |
44 |
61 |
64 |
71 |
83 |
у |
26 |
9 |
10 |
11 |
6 |
33 |
31 |
26 |
30 |
44 |
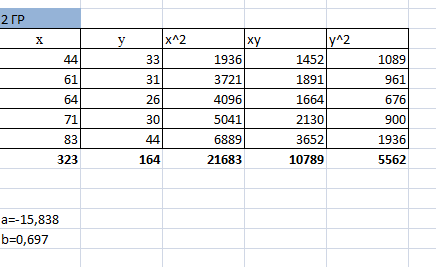
Разделим совокупность наблюдений на две группы и для каждой группы с помощью программы Анализ данных в EXCEL, инструмент Регрессия определим параметры уравнений регрессий и остаточные суммы квадратов.
Таблица 2.4
Расчётные значения
|
Уравнение регрессии |
Остаток |
1 группа |
|
|
2 группа |
|
|
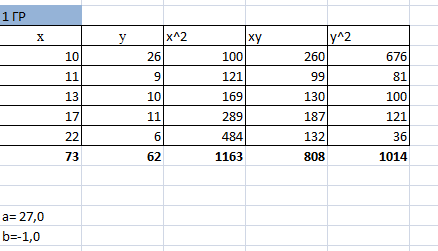
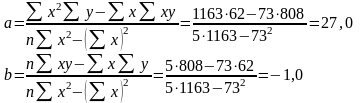
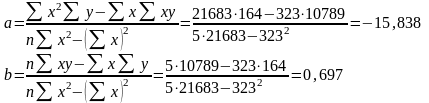
Расчетный
критерий равен:
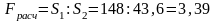 .
.
Табличное
значение F-критерия
с
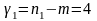 и
и
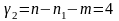 степенями
свободы и при доверительной вероятности
0,95
степенями
свободы и при доверительной вероятности
0,95
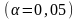 равно 6,39.
равно 6,39.
Величина
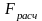 не превышает табличное значение
F-критерия,
следовательно, свойство гомоскедастичности
выполняется, остатки имеют постоянную
дисперсию. Модель по данному критерию
адекватна.
не превышает табличное значение
F-критерия,
следовательно, свойство гомоскедастичности
выполняется, остатки имеют постоянную
дисперсию. Модель по данному критерию
адекватна.
в) Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществим с помощью d-критерия Дарбина-Уотсона.
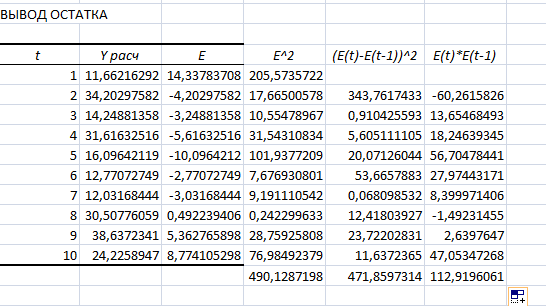
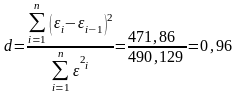 .
.
Расчетное
значение критерия сравнивается с нижним
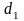 и
верхним
и
верхним
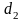 критическими
значениями статистики Дарбина-Уотсона.
При n=10
и уровне значимости 5%,
критическими
значениями статистики Дарбина-Уотсона.
При n=10
и уровне значимости 5%,
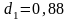 ,
,
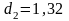 .
.
Поскольку
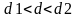 - область неопределенности, переходим
к расчету первого коэффициента
автокорреляции:
- область неопределенности, переходим
к расчету первого коэффициента
автокорреляции:
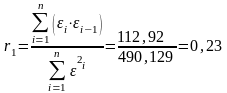
Расчетное значение критерия сравнивается с табличным значением r табл = 0,36.
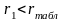 ,
то гипотеза о независимости остатков
принимается, автокорреляция в остатках
отсутсвует, и модель признается адекватной
по данному критерию.
,
то гипотеза о независимости остатков
принимается, автокорреляция в остатках
отсутсвует, и модель признается адекватной
по данному критерию.
г) Случайные отклонения далжны быть независимы от объясняющих переменных.
Так
как
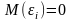 ,
то
,
то
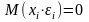
д) Проверку соответствия распределения остаточной последовательности нормальному закону распределения осуществим с помощью R/S-критерия. формуле:
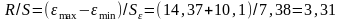 .
.
Расчетное значение R/S-критерия сравнивается с табличными значениями (нижней и верхней границами данного отношения).
Нижняя
и верхняя границы отношения при уровне
значимости
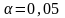 равны соответственно 2,67 и 3,57.
равны соответственно 2,67 и 3,57.
Расчетное значение отношения попадает в интервал между критическими границами, следовательно, с заданным уровнем значимости гипотеза о нормальности распределения принимается.
Выполним пункты 6)-8) для степенной модели

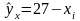
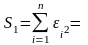 148
148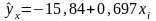
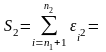 43,6
43,6