Раздзел 4. Метад геаметрычных пераўтварэнняў

§ 1. Выкарыстанне рухаў пры развязанні задач

Для некаторых задач дадзеныя на рысунку размешчаны нязручна, што абцяжоўвае пошук развязання. Калі пэўным чынам пераўтварыць рысунак, то схаваныя сувязі праявяцца, што дазволіць знайсці шлях развязання.

У залежнасці ад таго, што трэба захаваць, выбіраецца тое ці іншае пераўтварэнне.

Прыклад 1. Знайсці плошчу трапецыі з асновамі 10 і 7 і бакавымі старанамі 5 і 4 (рыс. 132).

Н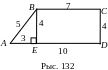 яхай у трапецыі АВСD, ВС // АD, АD = 10, ВС = 7, АВ = 5, СD = 4.

Зрушым СD на вектар , тады ВЕ = 4, АЕ = 10 – 7 = 3. Паколькі АЕ² + ВЕ² = АВ², то  АЕВ = 90. Значыць, ВЕ ёсць вышыня трапецыі. Таму

S = (ВС + АD)æВЕ = (7 + 10)æ4 = 17æ2 = 34.

Прыклад 2. Знойдзем плошчу трапецыі, у якой асновы роўныя 7 і 6, а дыяганалі – 5 і 12. (рыс. 133)

Н яхай АВСD трапецыя, ВС // АD, у якой АD = 7, ВС = 6, АС = 5, ВD = 12.

Зрушым СА на вектар , атрымаем адрэзак ВК. Паколькі КВ² + АD² = 25 + 144 = 169 = 13² = КD², то  КВD = 90. Значыць, S_КВD = КВæВD = æ5æ12 = 30. Плошча трапецыі АВСD роўная плошчы трохвугольніка, бо ў іх агульная вышыня, а КD = АD + ВС. Значыць, S_АВСD = 30.

Прыклад 3. На прамой l знойдзем пункт М такі, што ламаная АМВ мае найменшую даўжыню, А і В – дадзеныя пункты.

Н яхай пункты А і В знаходзяцца па розныя бакі прамой l (рыс. 134). Тады шуканы пункт М ёсць пункт перасячэння АВ з l. Калі ўзяць любы іншы пункт, то даўжыня ламанай АNВ будзе большай за даўжыню АМВ, у адпаведнасці з няроўнасцю трохвугольніка.

Няхай А і В ляжаць па адзін бок ад прамой l (рыс. 135). Адлюструем В сіметрычна адносна l, атрымаем пункт В₁. Паколькі АМ + МВ₁ = АМ + МВ, то пункт М ёсць шуканы пункт.

Прыклад 4. На старанах востравугольнага трохвугольніка АВС (рыс. 136), выбраць 3 пункты М, N, Р так, каб трохвугольнік МNР меў найменшы перыметр.

Н яхай пункты М, N, Р ёсць шуканыя пункты. Адлюструем пункт М адносна прамых ВА і ВС, атрымаем пункты М₁ і М₂. Тады перыметр трохвугольніка МNР роўны даўжыні ламанай М₁NРМ₂. Пры выбраным М даўжыня ламанай М₁NРМ₂ найменшая, калі пункты N і Р ляжаць на прамой М₁М₂. Цяпер вызначым, як трэба выбраць пункт М, каб перыметр быў найменшым.

Трохвугольнік М₁ВМ₂ ёсць раўнабокі, бо М₁В = ВМ = М₂В. Паколькі  М₁ВА =  АВМ, а  М₂ВС =  СВМ, то  М₁ВМ₂ = 2  АВС. Велічыня вугла М₁ВМ₂ не залежыць ад выбара пункта М.

Такім чынам, пры любым выбары пункта М трохвугольнік М₁ВМ₂ раўнабокі з вуглом М₁ВМ₂ роўным падвоенаму вуглу АВС. Аснова М₁М₂ найменшая, калі бакавая старана М₁В найкарацейшая, г.зн. калі адрэзак ВМ – найкарацейшы, г.зн. калі ВМ – вышыня. Такім чынам, М ёсць аснова вышыні, праведзенай з вяршыні В на старану АС.

Гэтак сама N і Р – асновы вышыняў, праведзеных з вяршыняў С і А.

Мы даказалі, што з усіх трохвугольнікаў, утвораных вяршынямі, выбранымі на старанах востравугольнага трохвугольніка найменшы перыметр у артатрохвугольніка гэтага трохвугольніка.

Прыклад 5. На трох дадзеных паралельных прамых a, b, c выбраць тры пункты, па адным на кожнай прамой, так, каб яны былі вяршынямі квадрата.

Р ашэнне. Дапусцім, што патрэбны квадрат PQRS пабудаваны (рыс. 137). Пры павароце на 90 вакол вяршыні P вяршыня Q пяройдзе ў вяршыню S, а разам з гэтым прамая a – у перпендыкулярную прамую a₁, што праходзіць праз пункт S. Адсюль зразумела наступнае развязанне задачы. Няхай P – пэўны пункт на прамой b. Прамую a паварочваем на 90 вакол пункта P.

Няхай a₁ прамой a пры гэтым павароце перасякае прамую c у пункце S. Пункт S ёсць другая вяршыня квадрата. Вобраз пункта S пры павароце вакол P на 90 у супрацьлеглым кірунку дае яшчэ адну вяршыню Q квадрата. Пасля гэтага знаходзім і чацвёртую вяршыню R.