Часть 2. Геометрия

Школьная геометрия (ШГ) знакомит с основными свойствами трёхмерного евклидового пространства, которые зафиксированы в аксиомах планиметрии и стереометрии. Эти свойства используются при изучении геометрических фигур, как основных, т.е. названных в самих аксиомах, так и новых, которые вводятся определениями. К основным фигурам в школьном учебнике относятся точка, прямая, плоскость, полупрямая, полуплоскость. Другие фигуры – отрезок, угол, треугольник, четырёхугольник, окружность и т.д. – вводятся через определение.

Школьная планиметрия знакомит с элементами теорий треугольника, четырёхугольника, окружности. В стереометрии рассматриваются взаимное расположение прямых и плоскостей, многогранники и тела вращения. Изучение декартовых координат, векторов, движения, подобия образует базу использования в геометрии кроме синтетического (его называют ещё методом разных треугольников) других методов: алгебраического, координатного, векторного, геометрических преобразований.

Наш курс элементарной геометрии направлен на усвоение основных методов в геометрии, которое будет связано с углублением и расширением знаний.

Раздел 1. Алгебраический метод

§ 1. Сущность алгебраического метода

Алгебраический метод применяется при решении задач, в которых по данным величинам нужно найти другие, искомые величины.

Задача 1. Стороны треугольника равны 5, 6, 8 (рис. 1). На сторонах длиной 5 и 6 выбраны точки М и N соответственно так, что ВМ : МА = 4 : 1, BN : NC = 1 : 2. Найти длину отрезка МN.

Р ешение.

Поскольку , , то ВМ =   = = = 4, ВN = =  = 2.

Из треугольника авс по теореме косинусов

АС = ВА + ВС – 2 ВА ВС соsВ,

или соsВ = = = – = – .

Из треугольника МВN по теореме косинусов:

МN = BM + BN – 2 BM BN cosB = 4 + 2 – 2 4 2 (– ) = 16 + 4 + = 20,8, откуда МN = 2 .

При решении задачи 1 проводилось поэтапное вычисление, при котором из данных величин через вычисления ряда промежуточных найдена искомая величина. При этом были использованы известные геометрические факты.

Задача 2. На сколько треугольных частей можно разрезать тысячеугольник, в котором отмечены 500 внутренних точек, если вершинами треугольников могут быть только вершины тысячеугольника и отмеченные точки.

Р ешение.

Пусть после разрезания возникло х треугольных частей. Сумма их внутренних углов равна 180 х. Поскольку до разрезания треугольников эти углы составляли все внутренние углы тысячеугольника и все полные углы с вершинами в отмеченных точках, то их сумма равна

180 (1000 – 2) + 360 500. Поэтому

180 х = 180 (1000 – 2) + 360 500,

или х = 998 + 1000, или х = 1998.

Отметим, что вместе с ответом на вопрос задачи, мы доказали, что количество частей – треугольников не зависит от способа разрезания.

При решении задачи 2 неизвестная величина найдена с помощью уравнения, которое было составлено с учетом условия задачи и известных геометрических фактов.

§ 2. Основные отношения школьной геометрии

Использование алгебраического метода основывается на связях между элементами фигур. Из школьного курса известно, что:

• сумма смежных углов равна 180 ;

• вертикальные углы равны;

• в равнобедренном треугольнике углы при основании равны;

• если в треугольнике два угла равны, то стороны против них также равны;

• в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

• сумма углов треугольника равна 180 ;

• внешний угол треугольника равен сумме внутренних углов, не смежных с ним;

• серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной около этого треугольника окружности;

• биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанной в этот треугольник окружности;

• при пересечении двух прямых а и b третьей прямой с внутренние накрест лежащие углы равны тогда и только тогда, когда а || b;

• противоположные стороны выпуклого четырёхугольника равны тогда и только тогда, когда этот четырёхугольник – параллелограмм;

• диогонали четырёхугольника точкой пересечения делятся пополам тогда и только тогда, когда этот четырёхугольник – параллелограмм;

• параллелограмм имеет равные диагонали тогда и только тогда, когда он – прямоугольник;

• параллелограмм имеет взаимно перпендикулярные диагонали тогда и только тогда, когда он – ромб;

• если на одной стороне угла параллельные прямые отсекают равные отрезки, то при пересечении их с другой стороной угла также возникают равные отрезки (теорема Фалеса);

• средняя линия треугольника параллельна третьей стороне и равна её половине;

• средняя линия трапеции параллельна основаниям и равна их полусумме;

• параллельные прямые отсекают на сторонах угла пропорциональные отрезки;

• в треугольнике квадрат большей стороны равен сумме квадратов двух других сторон тогда и только тогда, когда этот треугольник прямоугольный;

• для любых трёх точек А, В, С, лежащих на одной прямой, АВ = АС + СВ или АВ = АС – СВ;

• центральный угол окружности измеряется дугой, на которую опирается;

• вписанный в окружность угол измеряется половиной дуги, на которую опирается;

• произведение частей хорды, на которые она делится своей точкой М, одно и то же для всех хорд, проведённых через М;

• произведение секущей, проведённой через точку М, находящуюся вне окружности, на её внешнюю часть одно и то же для всех секущих, проведённых через М;

• квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними (теорема косинусов);

• стороны треугольника пропорциональны синусам противолежащих углов (теорема синусов);

• в треугольнике против большего угла лежит большая сторона;

• в треугольнике против большей стороны лежит больший угол;

• отношение длины окружности к её диаметру есть величина постоянная (константа), она обозначается ;

• для вычисления площадьи S некоторых фигур применяют формулы:

S_{прямоугольника} = ab, где а и b – измерения прямоугольника;

S_{параллелограмма} = аh, где а – сторона параллелограмма, h – высота к ней;

S_{треугольника} = аh, где а – сторона треугольника, h – высота к ней;

S_{треугольника} = аb sіnC, где а и b – стороны треугольника, С –угол между ними;

S_{треугольника} = , где а, b, c – стороны треугольника,

р = (а+b+c) –его полупериметр;

S_{трапеции} = h, где а и b – основания трапеции, h – проведённая к ним высота;

S_круга =  r² , где r – радиус круга;

S_{сектора} = , где r – радиус сектора,  – его градусная мера;

• R = , r = , a, b, c – стороны треугольника, S – его площадь, R и r – радиусы описанной около него и вписанной в него окружностей соответственно;

• площади подобных фигур относятся как квадраты их линейных размеров;

• S_пр = S₀ cos , где S₀ – площадь фигуры Ф, размещённой в плоскости , S_пр – площадь ортогональной проекции фигуры Ф на плоскость ,  – двугранный угол между плоскостями  и ;

• противолежащие грани параллелепипеда параллельны и равны;

• диагонали параллелепипеда пересекаются в одной точке и делятся ей пополам;

• квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений;

• для вычисления боковых поверхностей тел применяются формулы:

  • S_{бок.цилиндра} = 2 rh, где r – радиус основания цилиндра, h – его высота;

  • S_{бок. конуса} =  rl, где r – радиус основания конуса, l – его образующая;

  • S_шара = 4 r² , где r – радиус шара;

• для вычисления объёмов тел применяют следующие формулы:

  • V_{прямоуг.параллелепипеда} = abc, где a, b, c – измерения прямоугольного параллелепипеда;

  • V_призмы = S_осн.Н, где S_осн. – площадь основания призмы, Н – её высота;

  • V_{пирамиды} = S_осн.Н, где S_осн. – площадь основания пирамиды, Н – её высота;

  • V_{усеч. пирамиды} = _. Н (S₁ + S₂ + ), где H – высота усечённой пирамиды, S₁, S₂ – площади её оснований;

  • V_{цилиндра} =  r²H, где r – радиус основания цилиндра, H – его высота;

  • V_конуса = _.  r²Н, где r – радиус основания конуса, H – его высота;

  • V_{усеч. конуса} = _. Н (r₁² + r₁ r₂+r₂²), где H – высота усечённого конуса, r₁ и r₂ – радиусы его оснований;

  • V_шара =  R³, где R – радиус шара;

  • V_{шар. сегмента} =  Н²(R – ), где R – радиус сегмента, H – его высота;

  • V_{шар. сектор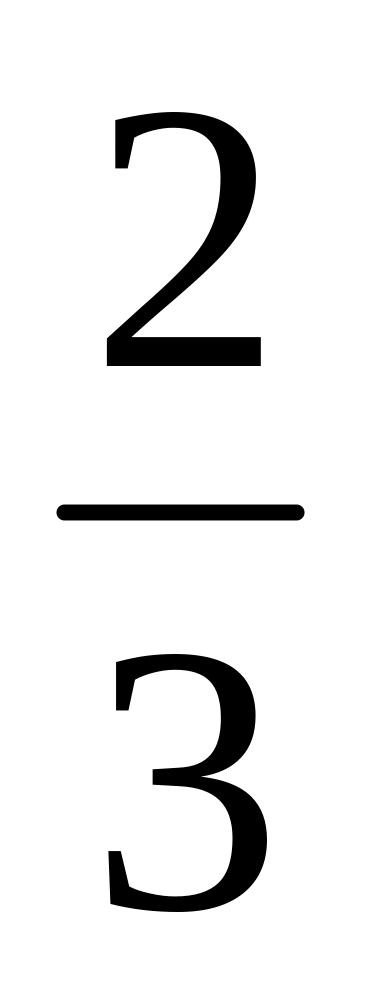а} = R²Н, где R – радиус сектора, H – высота соответствующего шарового сегмента;

• объёмы подобных тел относятся как кубы их линейных размеров.