1.5.4. Аналіз кластер-кластерного агрегування електропровідних полімерів

Процедура, подібна до вищеописаної, використовується також для визначення фрактальної розмірності електропровідних полімерів. Її особливістю є використання зображень, одержаних методом скануючої електронної мікроскопії. СЕМ-зображення після комп’ютерної обробки перетворюють у двокольорові і лише тоді аналізують щодо фрактальних характеристик полімерного шару, використовуючи як і у випадку кремнезему, модельну сітку. Зокрема фрактальна природа добре прослідковуються для тонких (3–4 мкм) плівок провідного політіофену з нанотрубчастою структурою (рис. 1.40, а–б) [40]. Результат комп’ютерної обробки цих зображень наведено на (рис. 1.40, в–г). Однак виявилося, що фрактальні характеристики морфології поверхневої плівки суттєво залежать від вибраного порогового значення k при перетворенні одержаного сірого 256-кольорового зображення. Це означає, що окремий (сірий) піксель на зображенні під час комп’ютерної обробки буде сприйматися як чорний (буде віднесений до субстрату) за умови, що його насиченість l буде більшою порівняно k, і навпаки, при k > l він вважатиметься білим (буде віднесений до полімеру). Залежність фрактальної розмірності від порогового значення k можна виразити наступною функцією

,

(1.108)

а б

в г

Рис. 1.40. СЕМ-зображення поверхневої мікроструктури тонких шарів нанотрубок провідного політіофену (збільшення у 9000 (а) та 20000 (б) разів), а також їхнє чорно-біле зображення після комп’ютерної обробки [40]

де n – так звана ідеальна фрактальна розмірність;  і А – підгоночні коефіцієнти. Тож, як випливає з наведеної формули, величина D_fr зростає зі збільшенням порогової величини сірого забарвлення для СЕМ-зображення.

Ще один підхід було реалізовано для аналізу фрактальності поліаналінових мікростержнів [41]. Він ґрунтується на припущенні, що процес електрохімічної полімеризації залежить від перенесення заряду вздовж макромолекулярного ланцюга, а тому електрична провідність лінійних макромолекулярних ланцюгів вища ніж для ланцюгів з розгалуженою структурою. Розгалуження зумовлюють стеричні перешкоди, які відповідають за зменшення перекривання -орбіталей і, як результат, за підвищення опору протіканню електричного струму вздовж ланцюга.

Ймовірність приєднання мономерної ланки С₆H₄N до ростучого ланцюга пропорційна 1 / R_ef, де R_ef ефективний опір у розглянутій точці. На практиці визначальну роль для характеристики фрактальної структури відіграє відношення R / R₀

де R₀ та R – опір незбуреного ланцюга та опір при його поодинокому розгалуженні відповідно. Це дає змогу оцінити фрактальну природу провідного полімерного ланцюга, використовуючи електричні схеми-аналоги.

Зокрема, модель росту поліанілінового ланцюга з розгалуженнями і, відповідну йому, електричну схему зображено на рис. 1.41. Нехай ймовірність лінійного

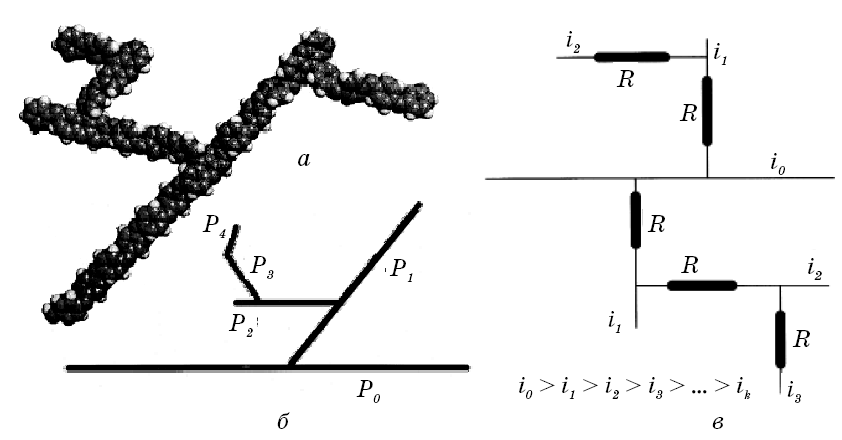
Рис. 1.41. Макромолекулярний ланцюг (а), мономерні ланки в структурі поліаніліну (б) і електрична схема фрактального росту поліаніліну (в)

приєднання мономерної ланки до зростаючого ланцюга становить P_i–1, тоді як ймовірність утворення нового розгалуження становитиме Р_і. Тут індекс і означає порядок розгалуження. Тоді для розгалуження першого порядку можна записати

,

(1.109)

або, в загальному випадку,

.

(1.110)

Відношення R / R₀, окрім ймовірності розгалуження, також характеризує швидкість реакції в новій гілці.

Фрактальна структура поліаніліну розраховувалась в широких межах зміни R / R₀ – від 1 до 100. Було знайдено, що генеровані комп’ютером електричні моделі можуть бути віднесені за формою до мікростержнів при R / R₀ = 5, 9, 16, 18 і 19, або до наноструктур при R / R₀ = 2–5 та 18. При цьому величина фрактальної розмірності D_fr, розрахована на основі електричних моделей, збігається з даними тунельної електронної мікроскопії і становить 1,69 та 1,88 для мікростержів (R / R₀ = 1 та 9) та для наноструктур (R / R₀ = 5) відповідно.