1.5.2. Фрактальна розмірність і методи її визначення

Теорію фракталів можна використати для аналізу як процесів, так і синтетичних (штучно створених) чи складних природних (ензими, протеїни, ДНК тощо) об’єктів: Недивлячись на невизначеність фрактальної розмірності процесу, фрактальний підхід успішно використовують для аналізу хімічних, електрохімічних і сорбційних процесів. Серед фрактальних наноструктур умовно можна виділити два типи об’єктів, а саме, регулярні і нерегулярні. Регулярні фрактали володіють симетрією самоподібності, тобто інваріантні до зміни форми у всіх напрямках. Ці об’єкти самовідображаються після зміни їхніх розмірів. В свою чергу нерегулярні фрактали неінваріантні відносно більшості операцій симетрії, наприклад, обертання чи відображення в просторі Евкліда, і не відображаються самі на себе при зміні довжини шкали. Їх ще називають статистично самоподібними фракталами, оскільки всі статистичні величини, які їх характеризують, інваріантні до зміни масштабу.

Статистично самоподібні фрактали придатні для моделювання лімітованих дифузією процесів кластер-кластерного агрегування, коли більші кластери утворюються в результаті об’єднання менших за розміром частинок [39]. Процес агрегування можна уявити як заповнення частинками центрів квадратної ґратки розмірами LL, яке відбувається за законом випадку. Приймають, що сусідні зайняті центри належать одному і тому ж кластеру, а сам він може переміщатися в одному з чотирьох рівноймовірних напрямів у двовимірному просторі (у центри сусідніх квадратних комірок).

Загалом для статистично самоподібного фракталу критерій µ(l) в межах відстані l від точки на фрактальному об’єкті задається співвідношенням

.

(1.97)

Тут µ(Y) – критерій для зайнятої області розміром Y; Λ – стала, що залежить від типу описуваного процесу; D_fr – фрактальна розмірність. Параметр µ(l) може, зокрема, відповідати загальній масі М, а характеристична довжина l –загальному розмірові об’єкта L. В цьому випадку рівняння (1.97) набуде вигляду

,

(1.98)

де Λ_M – амплітуда або фактор форми, пов’язаний з лакунарністю (про що йтиметься далі), а m – маса складової частинки розміром Y. Ця масштабуюча залежність між масою і розмірами подібна до відповідної масштабуючої залежності (М  L^d) для евклідових об’єктів у евклідовому просторі, коли розмірність d може дорівнювати 1, 2 та 3. З рівняння (1.98) слідує, що фрактальна розмірність пов’язана з кількістю частинок N розміром Y на відстані L від точки на об’єкті визначається співвідношенням

.

(1.99)

Один з найпростіших методів визначення фрактальної розмірності ґрунтується на тому, що фрактал, будучи у d-вимірному просторі Евкліда, є покритий d-вимірною сіткою з розмірами комірок l. Тоді фрактальна розмірність еквівалента ємності сітки, яка визначається кількістю зайнятих частинками місць у сітці

,

(1.100)

де N(l / L) – кількість заповнених елементів сітки. Однак стану, коли l→0, практично неможливо досягнути, тому оцінити D_fr можна, вимірявши залежність log (N(l / L)) від log (l / L) в інтервалі l₁ < l < l₂, де l₁ >Y (нижня межа), а l₂ < L (верхня межа):

.

(1.101)

Амплітуда (або фактор форми) Λ_М кількісно характеризує так звану лакунарність (від сл. лакуна – вільна порожнина): фрактали з більшою величиною амплітуди Λ_М заповнюють простір більш однорідно і тоді кажуть, що він менш лакунарний, тобто, у ньому є менше пустот. Як поняття лакунарності, так і фрактальної розмірності необхідно вживати для того, щоб знати як фрактальні об’єкти заповнюють простір, а також для повнішої характеристики геометрії об’єкта. Крім того, для багатьох реальних об’єктів є верхня межа характеристичної довжини ξ, яка може бути більшою порівняно з загальними розмірами об’єкта, але вище якої фрактальний масштаб більше не підтримується. Ця верхня межа є так званою кореляційною довжиною, вище якої структуру можна вважати однорідною і евклідовою. Фрактальність виникає для рівнів, нижчих від кореляційної довжини, і тоді рівняння (1.99) набуває вигляду

,

(1.102)

де Λ_М – лакунарність, а параметр n враховує кількість (статистичних) копій фрактальної області, які містить об’єкт загальним розміром L . Для реальних об’єктів при визначенні фрактальної розмірності використовують сітки з квадратними чарунками розмірами l / ξ, а кількість комірок N_T, потрібна для заповнення усієї сітки, становитиме

,

(1.103)

Ділення (1.102) на (1.103) дає вираз

,

(1.104)

згідно з яким фрактальна розмірність (для l<ξ) виразиться співвідношенням

.

(1.105)

Кореляційну довжину можна оцінити, використовуючи автокореляційну функцію С(s), яка виражає ступінь кореляції у наборі послідовних експериментальних даних (x_n). Детальніше, означаючи _n як

(1.106)

матимемо

.

(1.107)

Тут середні значення, наведене у дужках , означають усереднення набору експериментальних даних {x_n}, який еквівалентний множині місць у модельній сітці. В контексті модельних сіток, (x_n) відповідає ступеню заповнення у наборі x_n. Ступінь заповнення дорівнює одиниці, якщо місце зайняте, і, навпаки, незайняті місця характеризуються нулем. Характеристичними величинамими цієї функції є значення С при s = 1 та значення s, коли С(s)=0. Перша величина характеризує ступінь кореляції, тоді як друга, відома як кореляційна довжина (ξ), характеризує протяжність лінійної кореляції. Якщо два фрактальні об’єкти ідентичні, то їх кореляційні довжини мають бути ідентичними.
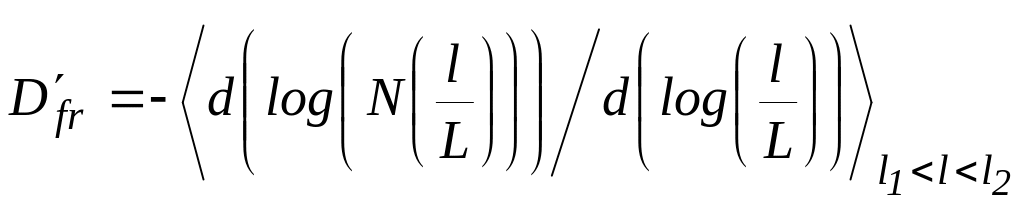