- •История развития чертежа.
- •Правила оформления чертежа ескд
- •Формат, рамка и основная надпись чертежа
- •Основная надпись на чертежах
- •Основная надпись на учебном чертеже
- •Масштаб
- •Шрифты чертежные
- •Линии чертежа
- •Разрезы, их отличие от сечений, виды разрезов
- •При выполнении разрезов на чертежах:
- •Виды Разрезов
- •Расположение видов на чертеже
- •Основные виды
- •Местные виды и виды с разрывами
- •Дополнительные виды
- •Выносные элементы
- •Шпоночные соединения. Виды шпонок: призматические, сегментные, клиновые
- •Шпоночное соединение: вал, ступица, призматическая шпонка
- •Шпоночное соединение призматической шпонкой
- •Призматические шпонки
- •Виды шпонок: призматическая, сегментная, клиновая
- •Основные типы сварных соединений[править | править исходный текст]
- •Заклепочные соединения. Виды заклепок. Расчет заклепок
- •Заклепка
- •Заклепочное соединение
- •Заклепки со сплошным стержнем, полупустотелые, пустотелые
- •Выполнение чертежа общего вида Чертеж
Шрифты чертежные
Все надписи на чертежах должны быть выполнены чертежным шрифтом. Начертание букв и цифр чертежного шрифта устанавливается стандартом. Стандарт определяет высоту и ширину буки и цифр, толщину линий обводки, расстояние между буквами, словами и строчками. Стандарт устанавливает десять размеров шрифта: 1,8; 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. За размер шрифта принимается величина, определяющая высоту прописной (заглавной) буквы. Шрифт может быть выполнен как с наклоном в 75°, так и без наклона.
Прописные буквы. Высота прописной буквы (h) равна размеру шрифта. Нижние элементы букв Д, Ц, Щ и верхний элемент буквы Й выполняются за счет расстояний между строками. Толщину линии шрифта (d) выбирают равной 0,1 h. Используя названные параметры (h, 0,lh), выстраивают вспомогательную сетку, в которую вписывают буквы. Ширина большинства прописных букв (g) равна 0,6h или 6d, что примерно соответствует размеру h ближайшего наименьшего номера шрифта. Исключение составляют буквы А, Д, М, X, Ц, Ы, Ю, ширина которых равна 0,7d, ширина букв Ж, Ф, Щ, Ш, Ъ принимается за 0,8d, а ширина букв Г, 3, С составляет 0,5d.
Строчные буквы. Высота большинства строчных букв (с) равна 0,7h, что примерно соответствует размеру (h) ближайшего наименьшего номера шрифта. Например, для шрифта № 10 высота строчной буквы будет равна 7 мм, а для размера № 7 — 5 мм. Верхние и нижние элементы строчных букв выполняются за счет расстояний между строками и выходят на величину 3d. Ширина большинства строчных букв равна 5d. Ширина букв а, м, ц, ъ равна 6d, букв ж, т, ф, ш, щ, ы, ю — 7d, а букв з, с — 4d.


При написании чертежного шрифта следует усвоить следующие правила:
1. Все надписи на чертеже должны быть выполнены от руки.
2. Высота букв, цифр и знаков на чертежах должна быть не менее 3,5 мм.
3. Начертание букв выполняйте по частям. Движение руки при выполнении прямолинейных элементов букв осуществляется сверху вниз или слева направо, а закругленных — движением вниз и влево или вниз и вправо.
4. Одинаковые элементы различных букв, цифр, знаков следует выполнять одним и тем же приемом, что способствует выработке автоматизма при их написании.
5. Выдерживайте заданный наклон шрифта с помощью направляющих штрихов.
6. Строго соблюдайте конструкцию каждой буквы и соотношение высоты и ширины буквы.
7. Старайтесь выдерживать такое расстояние между буквами, чтобы зрительно оно казалось одинаковым.
8. Четкость, ясность и удобство чтения чертежа зависят от качества его выполнения и правильного выбора размеров шрифта.
9. Все надписи на чертеже должны быть аккуратными.
Линии чертежа
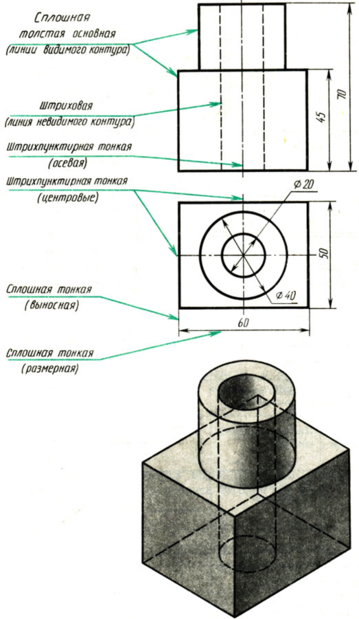
Чертеж и наглядное изображение детали имеют различные линии. Одни из них изображают реально существующие поверхности - видимые и невидимые контуры. Другие линии показывают размеры предмета, плоскости симметрии и т. п.; их нельзя увидеть на детали, так как это условные линии, которые не показывают реальных очертаний предмета. Очевидно, что условные линии должны по начертанию отличаться от линий, изображающих контуры детали.
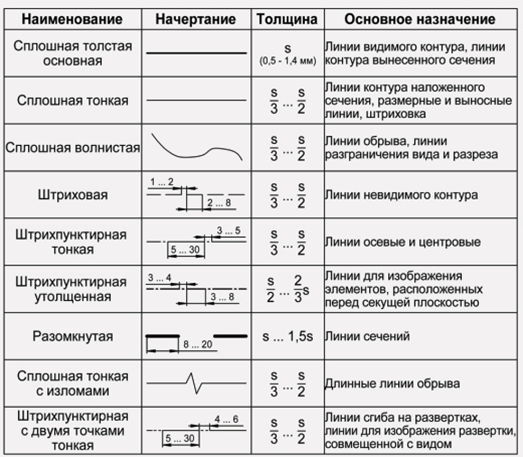
Сплошная толстая основная линия. Для изображения видимых контуров предметов применяется линия, называемая сплошной толстой основной. Толщина этой линии, обозначаемая латинской буквой s, установлена стандартом в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения. Выбранная толщина s линии должна быть одинаковой для всех изображений на данном чертеже.
Такой линией обведено изображение видимых очертаний предмета на рис.
Штриховая линия. Для невидимых очертаний предмета применяют линию, которую называют штриховой. На рис. такой линией показано невидимое на данном изображении отверстие, находящееся внутри детали. Штриховая линия состоит из штрихов (черточек) одинаковой длины. Их длина установлена стандартом в пределах от 2 до 8 мм (для ученических чертежей рекомендуется 4 мм). Длина всех штрихов в линии должна быть приблизительно одинаковой. Расстояние между штрихами должно составлять от 1 до 2 мм и быть приблизительно одинаковым в линии. Толщина штрихов зависит от выбранной толщины сплошной толстой основной линии и должна составлять от s/2 до s/3. Это означает, что толщина штриховой линии в 2-3 раза тоньше основной. Штриховые линии должны начинаться и заканчиваться штрихами. Неверно называть штриховую линию пунктирной. Раньше ее чертили в виде точек. По-немецки пункт означает точка, отсюда и название пунктирная. Теперь это название не соответствует характеру линии.
Штрихпунктирная тонкая линия. Для проведения осевых, а также центровых линий, указывающих центры окружностей и дуг, используют линию, называемую штрихпунктирной тонкой, которая состоит из длинных тонких штрихов и точек между ними. Длина штрихов от 5 до 30 мм, расстояние между ними от 3 до 5 мм (для учебных чертежей длину штрихов рекомендуют 20 мм). Толщину штрихпунктирной линии берут от s/2 до s/3.
Осевые и центровые линии концами должны выступать за контур изображения на 2-5 мм и оканчиваться штрихом, а не точкой. Положение центра окружности определяется пересечением штрихов.
Вычерчивание деталей надо начинать с проведения осевых и центровых линий, являющихся основой чертежа. С их помощью удобно строить симметричные изображения, откладывая от этих линий размеры, по которым вычерчивают контуры предмета.
Штрихпунктирная с двумя точками тонкая линия показывает линии сгиба на развертках и крайние положения подвижных предметов. Длина штрихов от 5 до 30 мм, расстояние между ними от 4 до 6 мм.
Сплошная тонкая линия. Кроме перечисленных выше линий, на рис. помечены надписями размерные и выносные линии. Выносные линии служат для связи между изображением и размерными линиями, проведенными вне контура. Для размерных и выносных применяют линию, называемую сплошной тонкой, толщина которой должна находиться в пределах от s/3 до s/2.
Выносные линии должны выходить за концы стрелок размерной линии примерно на 1-5 мм.
Сплошные тонкие линии применяют также для штриховки в сечениях.
Нанесение размеров на чертежах |
|
Общие сведения. Чертёж без размеров даёт только представление о форме детали, но практического значения иметь не может, поэтому наиболее ответственной и важной частью составления рабочих чертежей, т. е. чертежей, по которым будет выполняться деталь, является правильное нанесение размеров. Ввиду этого нанесение размеров является самой ответственной частью работы конструктора при составлении им чертежей и представляет известную трудность для лиц, начинающих изучать машиностроительноечерчение. В практике нередко встречаются чертежи очень сложных деталей, и конструктору приходится решать самостоятельно вопрос о нанесении размеров в каждом отдельном случае. Для удачного решения таких вопросов, помимо знаний ГОСТ, требуется и производственный опыт. При нанесении размеров на чертёж необходимо соблюдать следующие требования, предусмотренные ГОСТ 3458-46. Нанесение размеров. Стандартом предусматриваются общие правила нанесения размеров на чертёж; правила простановки размеров в зависимости от выбора конструктивных и технологических баз указанным стандартом не устанавливаются.
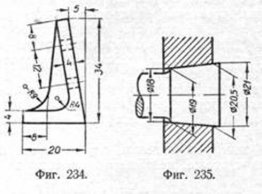
8. Размерные линии не должны служить продолжением линий контура, осевых, центровых и выносных. 9. Размерную линию следует проводить параллельно тому отрезку, размер которого указывается (фиг. 234).
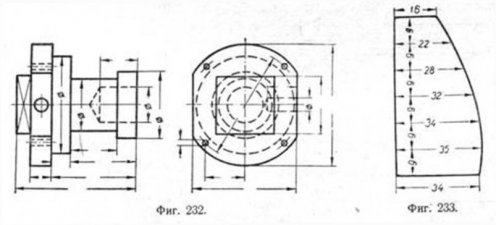
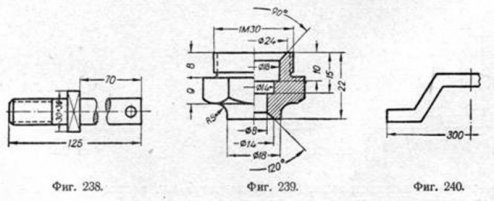
11. Размерные и выносные линии следует проводить тонкими, сплошными согласно ГОСТ 3456-46. 12. При отсчёте линейных размеров от некоторой базы размерные линии наносят параллельно (фиг. 232 и 236). Допускается проведение одной общей размерной линии по образцу фиг. 237. 13. При разрыве изображения размерную линию следует проводить полностью (фиг. 238). Если вид (или разрез) вычерчен только до оси симметрии (фиг. 239) или с обрывом (фиг. 240), то размерную линию проводят несколько дальше оси или линии обрыва.
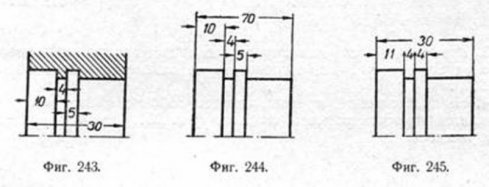
14. Стрелки, ограничивающие размерные линии, должны упираться острием в соответственные линии контура, осевые и т. п. Тип стрелки (в увеличенном виде) показан на фиг. 241. Величина стрелок выбирается в зависимости от толщины линии видимого контура (фиг. 242) и должна быть выдержана по возможности одинаковой для всего чертежа.
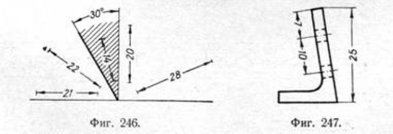
15. Если при нанесении размерного числа нет достаточного места для стрелок, то их ставят снаружи, обращая остриё к соответственным линиям контура, к выносным линиям и т. д. (фиг. 232, 234, 239, 243, 244 и др.). Допускается при последовательно-смежном размещении размерных чисел в случае недостатка места заменять некоторые стрелки на выносных линиях точками (фиг. 245).
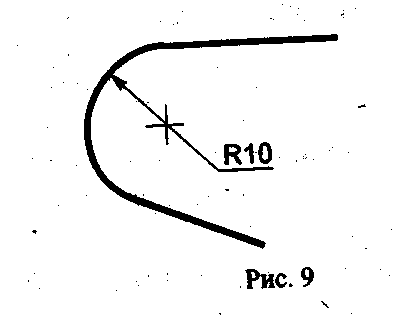
16. При указании размера радиуса дуги окружности стрелку следует ставить только у дуги; центр же дуги, если он не находится на пересечении осевых или центровых линий, допускается указывать маленьким кружком или точкой (фиг. 234) либо крестиком (фиг. 239).
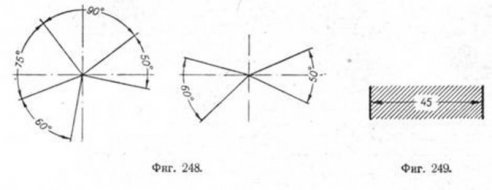
17. Цифры размерных чисел следует наносить вдоль размерных линий так, чтобы высота цифр располагалась перпендикулярно к этим линиям. Расположение цифр при различных наклонах размерных линий должно соответствовать фиг. 246. Следует, по возможности, избегать про-ведения размерных линий в пределах угла, отмеченного на фиг. 246 штриховкой; если этого избежать нельзя, то цифры следует располагать по общему правилу (фиг. 247).
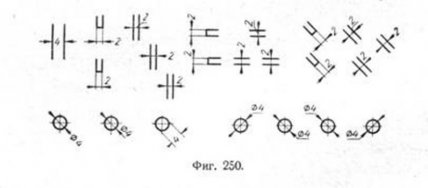
18. При указании размеров углов следует располагать цифры согласно примерам фиг. 248. 19. Если размерное число наносят на заштрихованном поле, то следует прерывать штриховку, но только в том месте, где вписывают цифры (фиг. 249). 20. Размерные числа не следует разделять или пересекать какими быто ни было линиями чертежа. Не допускается наносить размерные числа в месте пересечения двух размерных линий. В случае необходимости допускается прерывать осевую линию для нанесения размерного числа (фиг. 255). 21. В соответствующих случаях размерные числа можно наносить согласно примерам фиг. 250. 22. При нескольких параллельных между собой размерных линиях следует избегать расположения смежных размерных чисел одного под другим (фиг. 231, 239 и др.).
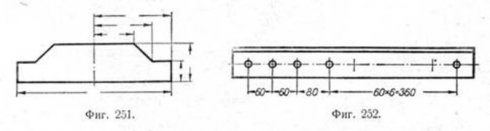
23. Размерные числа для внутренних и для наружных размеров детали следует, как правило, располагать по разные стороны изображения (фиг. 239). 24. На изображении, представляющем собой симметричную фигуру, допускается наносить размеры согласно фиг. 251. Для тел вращения это не допускается.
25. При расположении ряда одинаковых элементов (например, отверстий) на равных расстояниях друг от друга предпочтительно заменять длинные размерные цепочки числовыми указаниями (фиг. 252) или соответственной надписью.
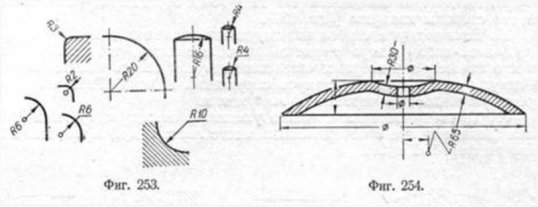
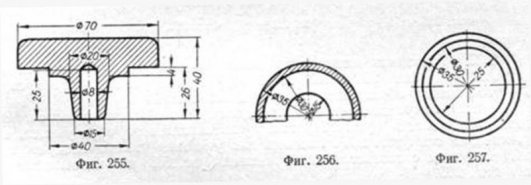
26. Размерные числа для радиусов следует дополнять обозначением R по типу R10. Располагать стрелку с внешней стороны дуги рекомендуется при размере радиуса (на чертеже) менее 6 мм (фиг. 253). 27. Когда центр дуги окружности из-за отсутствия места или при большой величине радиуса не может быть указан в пределах чертежа без нарушения масштаба, но показать положение центра необходимо для его координирования, размерную линию для нанесения размера радиуса следует изображать согласно фиг. 254.
28. Нанесение условного знака ? перед размерным числом для обозначения диаметра обязательно, если: а) отсутствует проекция на плоскость, перпендикулярную к оси изображаемой поверхности вращения (фиг. 255);
б) размерная линия для диаметра проведена с обрывом (фиг. 256 и 257) независимо оттого, изображена ли окружность неполностью (фиг. 256) или полностью (фиг. 257); в) размерное число вынесено за пределы окружности без выносных линий (фиг. 250);
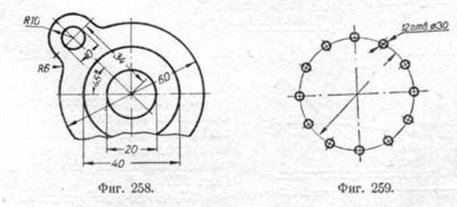
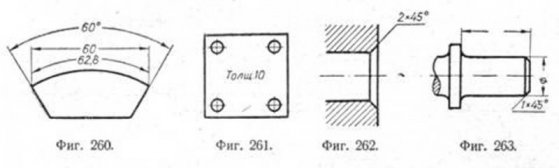
г) размер диаметра указан не на том виде или разрезе, на котором имеется проекция в форме окружности (фиг. 231). В случаях, аналогичных приведённым на фиг. 258 (размеры диаметров 10, 20, 40, 60), наносить знак диаметра не обязательно. 29. Повторяющиеся одинаковые отверстия могут быть указаны надписью, как изображено на фиг. 259. 30. Для указания длины дуги окружности размерную линию проводят в виде концентрической дуги (фиг. 260; для сравнения показана постановка размеров угла, его дуги и хорды этой дуги). 31. Квадрат обозначается по типу 30X30, где 30 — номинальный размер стороны квадрата (фиг. 238). 32. Если радиусы сгибов или скруглений одинаковы на всём чертеже или какой-либо радиус является преобладающим, то рекомендуется вместо нанесения размерных чисел для радиусов делать надписи по типу: „Радиусы сгибов 4 мм", „Радиусы скруглений 10 мм", „Радиусы сгибов, кроме указанных на чертеже, 4 мм" и т. п. 33. Толщину материала можно указывать наряду с другими способами (надписывание в определённом месте листа и др.) и так, как показано на фиг. 261 и 269.
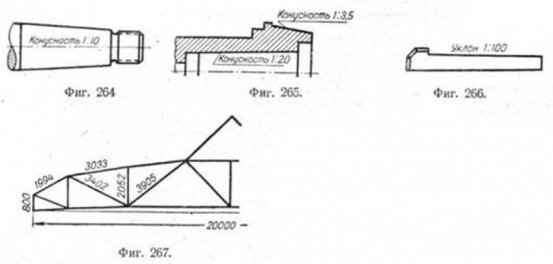
34. При указании конических фасок надписью рекомендуется её делать по типу фиг. 262 и 263, где 2 и 1— высота усечённого конуса, а 45°—угол между образующей конуса и его осью. 35. Если конусность указывают надписью, то её следует располагать вдоль осевой линии (фиг. 264) или у соответственной образующей, но параллельно оси (фиг. 265). Надпись для указания уклона следует располагать рядом с соответственной линией (фиг. 266) или на выноске по типу фиг. 265.
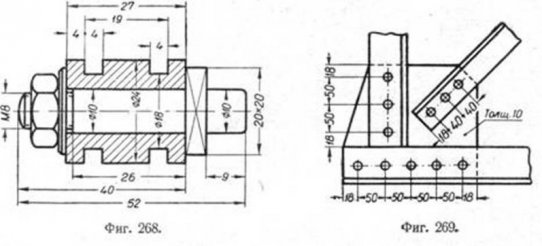
36. При схематическом изображении металлических конструкций размеры длин отдельных стержней проставляют без выносных и размерных линий, как показано на фиг. 267. 37. В случае указания размеров смежных деталей в сборочном чертеже следует чётко разграничивать размеры одной детали от размеров другой (фиг. 268). Исключение допускается для размеров, являющихся общими (фиг. 269).
|
|||
|
|||
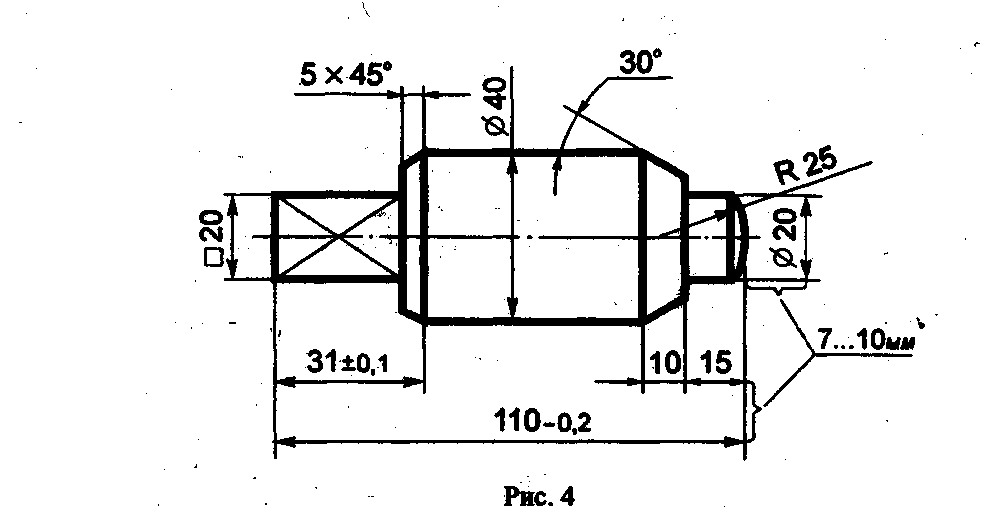
ОСНОВНЫЕ ПРАВИЛА НАНЕСЕНИЯ РАЗМЕРОВ НА ЧЕРТЕЖАХ (ВЫНОСНАЯ ЛИНИЯ, РАЗМЕРНАЯ ЛИНИЯ, СТРЕЛКИ, ЗНАКИ ДИАМЕТРА, РАДИУСА, РАСПОЛОЖЕНИЕ РАЗМЕРНЫХ ЧИСЕЛ) Величину изображённой детали можно определять только по размерным числам. Их наносят над размерными линиями возможно ближе к их середине (рис. 4).
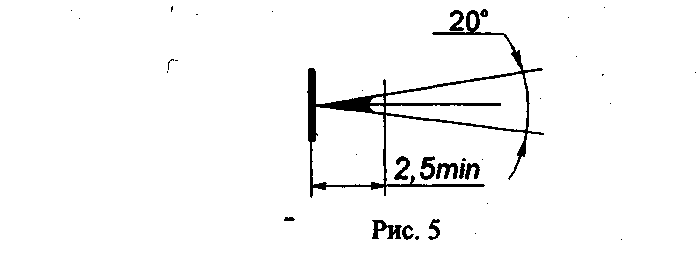
Размерные линии 'Ограничивают стрелками, которые остриём должны касаться выносных линий (размеры 110, 30, 15, 0 20 и другие на рис. 4), линий контура (размер 040) или осевых линий. Размерную линию следует проводить параллельно отрезку, размер которого указывают по возможности вне контура изображения. Расстояние между параллельными размерными линиями и от размерной линии до параллельной ей линии контура берут от 7 до 10 мм. Нельзя допускать, чтобы размерные линии пересекались с выносными или являлись продолжением линий контура, осевых, центровых и выносных. Запрещается использовать линии контура, осевые, центровые и выносные в качестве размерных. Чтобы размерные линии не пересекались с выносными, меньший размер наносят ближе к изображению, а больший - дальше (размеры 15, 30 и размер 110 на рис. 4). Форма стрелки показана на рис. 5. Размер стрелок следует выдерживать приблизительно одинаковым на всём чертеже.
Каждый размер на чертеже указывают только один раз. Размерные числа линейных размеров наносят в соответствии с положением размерных линий, как показано на рис. 6. Если размерная линия вертикальная, то размерное число ставят справа (рис. 6а). На наклонных размерных линиях цифры пишут так, чтобы они оказались в удобном для чтения положении, если дать размерной линии "упасть" в горизонтальное положение, как это указано стрелками на рис. 6 а, б, в.
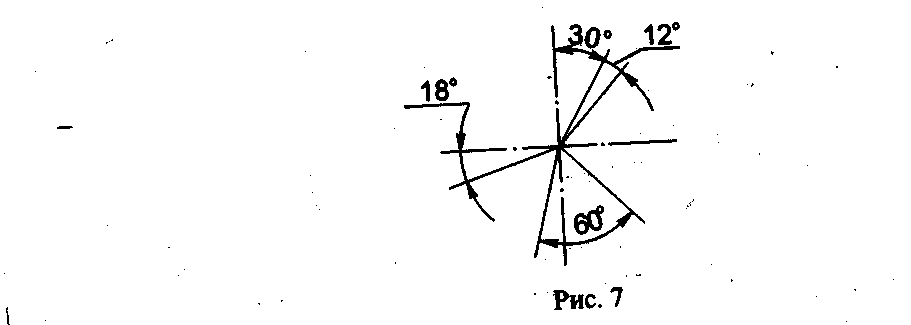
Линейные размеры на машиностроительных чертежах указывают в миллиметрах; если размеры нанесены у изображений, то единицы измерений (мм) не проставляют (см. рис.4). Угловые размеры наносят, как показано на рис. 7. Их указывают в градусах (°), минутах (') и секундах ("), проставляя единицы измерения, например, размер 30° на рис. 7. Размерную линию при этом проводят в виде дуги окружности с центром в вершине угла.
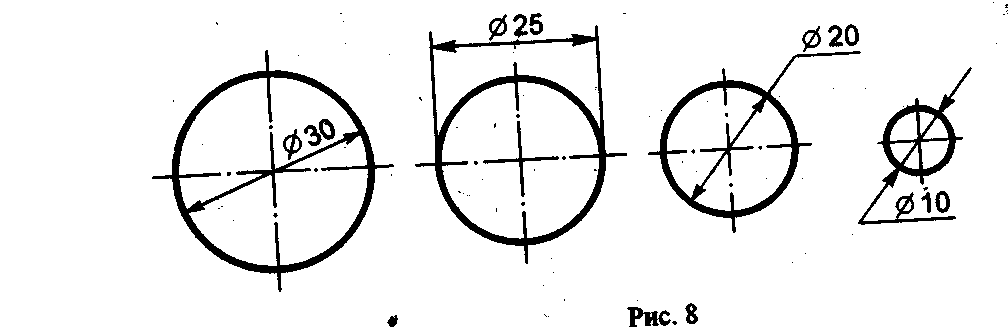
Для обозначения диаметра перед размерным числом во всех случаях наносят знак - кружок, перечеркнутый прямой линией под углом 75°. Применение и построение этого знака показано на рис. 8.
Если деталь имеет несколько одинаковых отверстий или других элементов (кроме скруглений), то наносится размер одного из них, а количество отверстий или других элементов указывают перед размерным числом, например 3 отв. 16 (рис. 10а).
Размеры толщины или длины детали, форма которой задана одним видом, наносят, как показано на рис. 10. Перед числом, указывающим толщину детали, наносят букву S, а перед числом, указывающим длину детали, - букву L |
|||
|
Деление отрезков и построение углов. Чтобы разделить отрезок АВ на несколько равных частей, из его конца, например из точки А, проводят под любым углом к нему произвольной длины прямую (рис. 55, а) . Из точки А по ней откладывают циркулем или линейкой столько равных частей, на сколько нужно разделить отрезок, например четыре. Соединяют точку 4 с точкой В прямой и проводят параллельные ей другие прямые через точки 3, 2, 1. Полученные точки 1 2 , 30 делят отрезок АВ на четыре равные части.
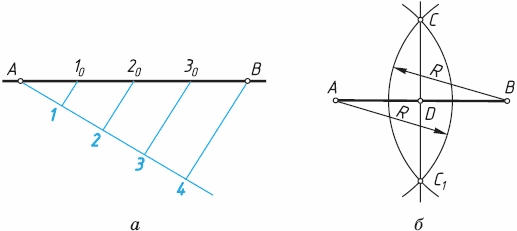
Рис. 55
Разделить отрезок на две равные части можно с помощью циркуля и линейки (рис. 55, б). Для этой цели из точек А и Б радиусом больше половины отрезка проводят дуги до их взаимного пересечения в точках С и С1. Соединив эти точки прямой, получим в пересечении ее с отрезком АВ точку D, которая является серединой заданного отрезка.
Построение различных углов, например в 45°, 60°, лучше выполнять с помощью угольников. Но строить углы, как и делить их на равные части, можно и с помощью других инструментов. Такие графические построения рассматриваются в геометрии.
Построение сопряжений линий. Контуры многих деталей (рис. 62) имеютплавные переходы одной линии в другую - кривой в прямую, одной кривой в другую и др. Такие плавные переходы называют сопряжениями. Точки, в которых одна линия переходит в другую, называют точками сопряжений (точки А и Б на рис. 63). Центры, из которых проводят дуги для построения сопряжений, называют центрами сопряжений. Радиус дуги, с помощью которой осуществляют построение сопряжения, называют радиусом сопряжения.
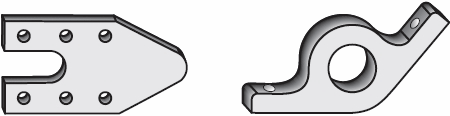
Рис. 62
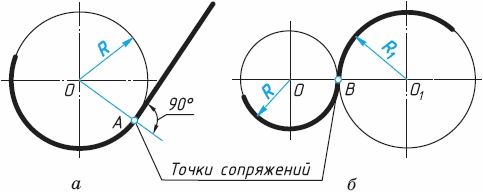
Рис. 63
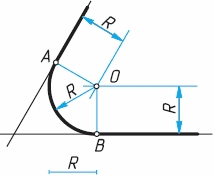
Рассмотрим некоторые примеры. Для построения сопряжения двух прямых линий, пересекающихся под любым углом (рис. 64), необходимо выполнить следующие построения.
Деление окружности на равные части. Некоторые детали имеют равномерно расположенные окружности или другие элементы, для построения которых нужно делить заданную окружность на равные части.
Для того чтобы разделить окружность на три равные части, нужно принять за центр точку пересечения окружности с одним из диаметров и провести из нее дугу, радиус которой R равен радиусу изображенной окружности (рис. 56, а). Полученные точки 1 и 3 вместе с точкой 2 разделяют заданную окружность на три равные части. Соединив точки 1, 2 и 3 прямыми, получим вписанный треугольник (рис. 56, б).
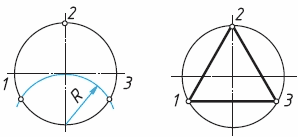
Рис. 56
Два взаимно перпендикулярных диаметра делят окружность на четыре равные части. Соединив точки 1, 2, 3 и 4 прямыми (рис. 57), получим вписанный четырехугольник.
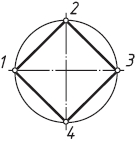
Рис. 57
На шесть равных частей окружность делят так. Приняв за центры дуг точки пересечения одного из диаметров с окружностью - А и В, проводят две дуги радиусом R, равным радиусу изображенной окружности (рис. 58, а). Эти дуги пересекают окружность в четырех точках 1, 2, 3 и 4. Вместе с точками А и Б они делят окружность на шесть равных частей (рис. 58, б). Ту же задачу можно решить при помощи угольника с углами 30° и 60° и линейки (рис. 58, в).
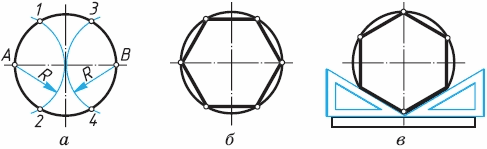
Рис. 58
На рисунке 59, а показано деление окружности на восемь равных частей. Для этой цели дуги 1-3, 3-5 и др. делят пополам точками 2, 4 и т. д. или делят на две равные части отрезки 1-3, 3-5 и т. д. Можно поступить так: провести через центр окружности две пары взаимно перпендикулярных диаметров (рис. 59, б).

Рис. 59
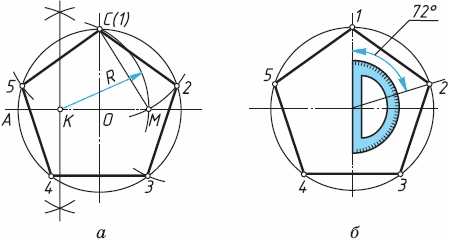
На пять равных частей окружность можно разделить с помощью циркуля и линейки (рис. 60, а). Если разделить радиус ОА окружности пополам (точка К), провести из точки К дугу радиусом КС до пересечения ее с диаметром окружности (точка М), то отрезок СМ и будет стороной вписанного пятиугольника. Последовательно откладывая полученный отрезок на окружности, можно получить точки, которые разделят окруж-ность на пять равных частей.
Эту графическую задачу можно решить и так: пятой части окружности соответствует угол в 72° (360°: 5 = 72°); такой угол можно построить с помощью транспортира (рис. 60, б).
Сопряжение |
|
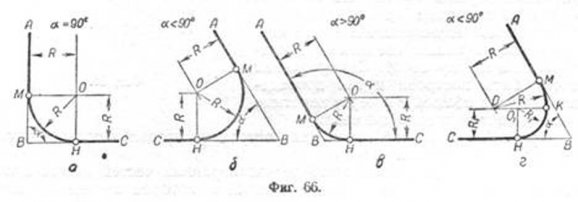
Сопряжением называется плавный переход по кривой от одной линии к другой. Сопряжения бывают циркульные и лекальные. Построение их основано на свойствах касательных к кривым линиям. Сопряжение отрезков прямых с циркульными кривыми будет возможно, если точка сопряжения является одновременно и точкой касания прямой к дуге кривой. Следовательно, радиус сопряжения должен быть перпендикулярным к прямой в точке касания. Сопряжение циркульных кривых возможно тогда, когда точка сопряжения будет являться одновременно и точкой касания сопрягаемых дуг. Следовательно, точка касания должна находиться на линии центров дуг окружностей. Сопряжение пересекающихся прямых: Пример 1. Даны пересекающиеся прямые AB и ВС и радиус сопряжения R; требуется выполнить сопряжение прямых (фиг. 66, а, б, в). Сопряжение будет возможным, если прямые AB и ВС будут касательными к окружности радиуса R. Для нахождения центра этой окружности
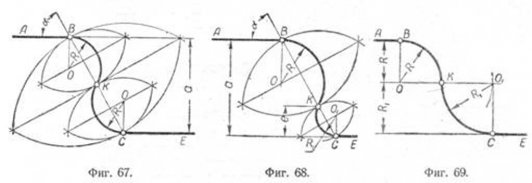
необходимо провести на расстоянии R параллельно заданным прямым вспомогательные прямые до их взаимного пересечения в точке 0. Из точки О, как из центра, проводится дуга радиуса R. Точками сопряжения будут точки M и Н, определяемые пересечением прямых AB и ВС с опущенными на них перпендикулярами из точки О. Пример 2. Даны пересекающиеся прямые AB и ВС и радиусы сопряжения R и R1 Построение сопряжения возможно, если угол а<90. Способ построения такого сопряжения приведён на фиг. 66,г. Сопряжение параллельных прямых Пример 1. Даны две параллельные прямые AB и СЕ и точки сопряжения В и С (фиг. 67). Надо построить плавное сопряжение циркульными кривыми так, чтобы оно проходило через заданную точку K, посредине отрезка ВС. Для определения радиусов и центров дуг сопряжения делим отрезки BK и КС прямыми так, чтобы они были перпендикулярны этим отрезкам и делили их пополам. Так как радиус сопряжения должен быть перпендикулярным к прямой в точке сопряжения, то для нахождения центров О дуг сопряжения восстанавливаем из точек В и С перпендикуляры до пересечения их с ранее проведёнными перпендикулярами к прямой ВС. Точки пересечения этих перпендикуляров определят положение центров сопряжений О—О, а равные между собой отрезки 05 и ОС дадут величины радиусов сопряжений. Пример 2 (фиг. 68), Этот пример отличается от предыдущего
тем, что точка К взята на прямой ВС произвольно, на некотором расстоянии e от прямой СЕ; следовательно, радиусы сопряжений R и R1— разные по величине. Ход построения сопряжений такой же, как и в предыдущем примере. П p и м e p 3. Даны: расстояние между двумя параллельными прямыми AB и СЕ, равное сумме сопрягаемых радиусов R и R1, и точка сопряжения В (фиг. 69). Для построения сопряжения проводим параллельно AB на расстоянии R вспомогательную прямую 0—01. Центр сопряжения 0 для радиуса R будет находиться на пересечении перпендикуляра, проведённого из точки В к вспомогательной прямой. Описывая из точки О дугу радиусом R, найдём точку К, из которой радиусом R1 делаем на вспомогательной прямой засечку, определяющую центр сопряжения O1. Из точки О1 опускаем перпендикуляр на прямую СЕ и, найдя точку сопряжения С, сопрягаем точки К и С дугой радиуса R1. Сопряжение дуги окружности с прямой
На ней будет находиться центр сопряжения 0, для определения которого проводим параллельно AB на расстоянии R1 вспомогательную прямую ее до пересечения с проведённой дугой. Соединив точки O1 и О, найдём точку сопряжения С. Для определения точки а опускаем из О1 перпендикуляр на AB. Далее, радиусом R1 из центра O1 сопрягаем точки а и С. Пример 2. Даны: дуга радиуса R, прямая AB и точка сопряжения а. Требуется найти точку сопряжения С и радиус сопряжения R1 (фиг. 71). Проводим через точку а перпендикуляр к AB, на котором откладываем вниз отрезок aK, равный R. Соединяем центр О с точкой К. Для нахождения центра сопряжения O1 проводим через середину отрезка OK перпендикулярную прямую, которая пересечётся с прямой aK в точке O1 Соединив О1 с О, найдём точку сопряжения С. Сопряжение дуг окружностей дугой окружности
<(C-(R+R1))/2. Во всех случаях решение задачи сводится к нахождению центра 02сопрягающей дуги радиуса R2 и точек сопряжения A и В.
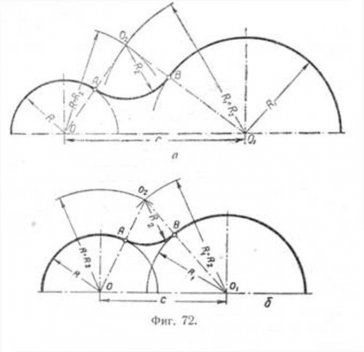
Внешнее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 72,a). Требуется построить сопряжение при условии, что C>R+R1. Для построения сопряжения необходимо определить центр 02 и точки сопряжения Л и В. Для нахождения центра 02 проводим из центра О дугу радиуса R2+R, а из центра О1 дугу радиуса R2+R1 Пересечение этих дуг определит центр 02. Соединив прямыми центры О и 01 с центром 02, найдём на пересечении этих прямых с соответствующими дугами точки сопряжения A и В. Полученные точки сопрягаем радиусом R2.
Построение сопряжения для случая, когда C<R+R1, дано на фиг. 72, б. Построение этого сопряжения ничем не отличается от предыдущего построения.
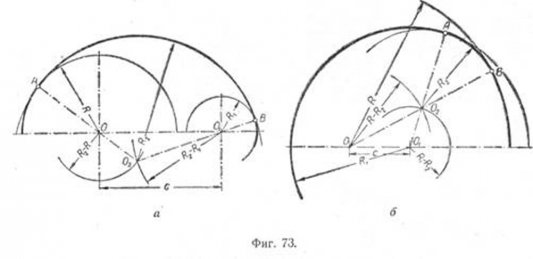
Внутреннее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 73, а). Требуется построить сопряжение, если C>R+R1 Решение этой задачи такое же, как и предыдущей, с той лишь разницей, что из центров О и О1 проводятся дуги радиусами R2 - R и R2 - R1. На фиг. 73, б приведено построение сопряжения для случая, когда C<R+R1. Это построение ничем не отличается от построения, приведённого в предыдущем примере (фиг. 73,a). |
Аксонометрическая проекция (греч. άχοπ — «ось» и «метрия») — способ изображения геометрических предметов на чертеже при помощи параллельных проекций. Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получается две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция. Стандартизированные аксонометрические проекции: - прямоугольная проекция (направление проецирования перпендикулярно к плоскости проекции): 1) прямоугольная изометрическая проекция; 2) прямоугольная диметрическая проекция; - косоугольная проекция (направление проецирования не перпендикулярно к плоскости проекции): 1) фронтальная изометрическая проекция; 2) фронтальная диметрическая проекция; 3) горизонтальная изометрическая проекция.

 10.
Выносные линии должны быть перпендикулярны
к размерной линии. Проведение выносных
линий под углом к размерной линии
(фиг. 235) допускается как исключение.
Выносные линии должны несколько
выходить за концы стрелок размерных
линий (приблизительно на 2 мм).
10.
Выносные линии должны быть перпендикулярны
к размерной линии. Проведение выносных
линий под углом к размерной линии
(фиг. 235) допускается как исключение.
Выносные линии должны несколько
выходить за концы стрелок размерных
линий (приблизительно на 2 мм).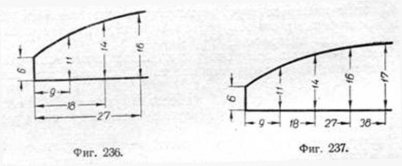
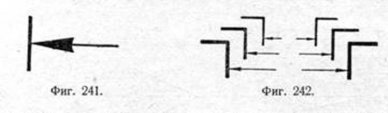
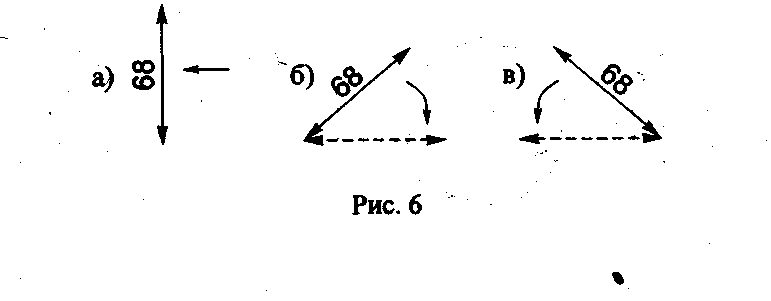
 Для
обозначения радиуса перед размерным
числом всегда наносят знак R -
латинская прописная буква (см. рис.
4). Стрелку наносят с одной стороны
(см. рис. 9)
Для
обозначения радиуса перед размерным
числом всегда наносят знак R -
латинская прописная буква (см. рис.
4). Стрелку наносят с одной стороны
(см. рис. 9)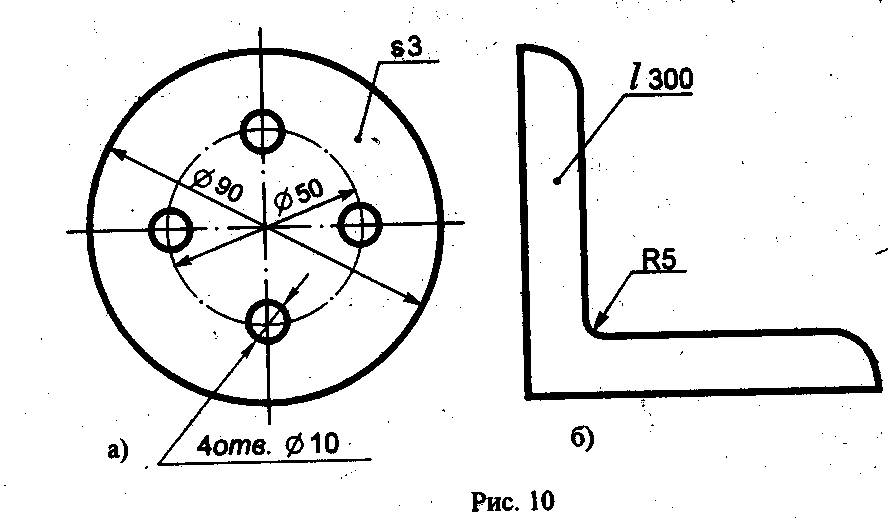
 Пример
1. Построим сопряжение дуги радиуса R
с прямой AB радиусом R1 (фиг. 70). Для этого
необходимо найти центр сопряжения 0
и точки сопряжения С и а. Точка С
является одновременно точкой их
касания и должна лежать на линии
центров этих дуг. Радиус сопряжения
должен быть перпендикулярен к прямой
AB в точке касания а. Поэтому из центра
О описываем радиусом, равным сумме
R+R1, дугу.
Пример
1. Построим сопряжение дуги радиуса R
с прямой AB радиусом R1 (фиг. 70). Для этого
необходимо найти центр сопряжения 0
и точки сопряжения С и а. Точка С
является одновременно точкой их
касания и должна лежать на линии
центров этих дуг. Радиус сопряжения
должен быть перпендикулярен к прямой
AB в точке касания а. Поэтому из центра
О описываем радиусом, равным сумме
R+R1, дугу.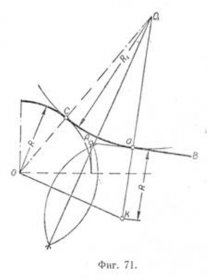 Сопряжение
дуг окружностей может быть внешним
(фиг. 72) или внутренним (фиг. 73). В
обоих случаях сопряжения выполнимы:
1) если расстояние С между центрами
О и 01 сопрягаемых
дуг больше суммы их радиусов R и R1 (фиг.
72, а и 73, а), т.е. C>R+R1 и 2) когда C<R+R1 (фиг.
72, б и 73, б). Сопряжение выполнить
невозможно, если один из радиусов
сопрягаемых дуг окажется большим или
равным сумме величины радиуса второй
сопрягаемой дуги и расстояния между
центрами сопрягаемых дуг, т. е. если
получится соотношение R>=C+R1 или
R1>=C+R. Для внешнего сопряжения дуг
сопряжение окажется также невозможно,
если радиус сопрягающей дуги R2 будет
меньше полуразности С — (R+R1), т. е. R2 <
Сопряжение
дуг окружностей может быть внешним
(фиг. 72) или внутренним (фиг. 73). В
обоих случаях сопряжения выполнимы:
1) если расстояние С между центрами
О и 01 сопрягаемых
дуг больше суммы их радиусов R и R1 (фиг.
72, а и 73, а), т.е. C>R+R1 и 2) когда C<R+R1 (фиг.
72, б и 73, б). Сопряжение выполнить
невозможно, если один из радиусов
сопрягаемых дуг окажется большим или
равным сумме величины радиуса второй
сопрягаемой дуги и расстояния между
центрами сопрягаемых дуг, т. е. если
получится соотношение R>=C+R1 или
R1>=C+R. Для внешнего сопряжения дуг
сопряжение окажется также невозможно,
если радиус сопрягающей дуги R2 будет
меньше полуразности С — (R+R1), т. е. R2 <