2.3 Види умовної ентропії

Вирізняють часткову та загальну умовні ентропії джерела повідомлень.

Часткова умовна ентропія - це кількість інформації, що припадає на одне повідомлення джерела X за умови встановлення факту вибору джерелом Y повідомлення y_j, або кількість інформації, що припадає на одне повідомлення джерела Y за умови, що відомий стан джерела X:

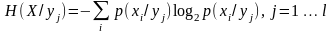, (1.16)

, (1.17)

де 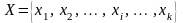, - алфавіти повідомлень; x_i - певне повідомлення джерела X, щодо якого визначається часткова умовна ентропія H(Y/x_i) алфавіту Y за умови вибору джерелом X повідомлення x_i; y_j - певне повідомлення джерела Y, щодо якого визначається часткова умовна ентропія H(X/y_j) алфавіту X за умови вибору повідомлення y_j; i - номер повідомлення з алфавіту X; j - номер повідомлення з алфавіту Y; p(x_i/y_j), p(y_j/x_i) – умовні імовірності.

Загальна умовна ентропія визначається так:

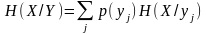, (1.18)

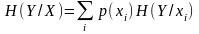. (1.19)

Отже, загальна умовна ентропія (1.18) - це середньостатистична кількість інформації (математичне сподівання), що припадає на будь-яке повідомлення джерела X, якщо відомий його статистичний взаємозв'язок з джерелом Y. Так само загальна умовна ентропія (1.19) - це середня кількість інформації, яка міститься в повідомленнях джерела Y за наявності статистичного взаємозв'язку з джерелом X.

З урахуванням (1.16), (1.17) та (1.7), (1.8) вирази (1.18), (1.19) набувають такого вигляду:

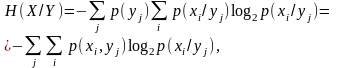, (1.20)

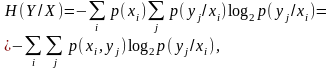, (1.21)

де p(x_i, y_j) - сумісна імовірність появи повідомлень x_i, y_j; p(x_i/y_j), p(y_j/x_i) – їх умовні імовірності.

Властивості умовної ентропії:

1) якщо джерела повідомлень X і Y статистично незалежні, то умовна ентропія джерела X стосовно Y дорівнює безумовній ентропії джерела X і навпаки:

H(X/Y)=H(X), H(Y/X)=H(Y);

2) якщо джерела повідомлень X і Y настільки статистично взаємозв'язані, що виникнення одного з повідомлень спричиняє безумовну появу іншого, то їхні умовні ентропії дорівнюють нулю:

H(X/Y)=H(Y/X)=0;

3) ентропія джерела статистично взаємозалежних повідомлень (умовна ентропія) менша від ентропії джерела незалежних повідомлень (безумовної ентропії):

H(X/Y)<H(X), H(Y/X)<H(Y).

З властивості 3 випливає поняття статистичної надмірності, обумовленої наявністю статистичної залежності між елементами повідомлення:

, (1.22)

де H(X/Y) - загальна умовна ентропія джерела X стосовно джерела Y; H(X) - безумовна ентропія джерела X.

З урахуванням виразу (1.5) загальна статистична надлишковість алфавіту джерела інформації визначається так:

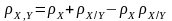. 1.23)

У разі малих значень 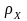, статистична надлишковість визначається виразом

. (1.24)

Наявність статистичної надмірності джерела інформації дозволяє використовувати кодування інформації, націлене на зменшення її надмірності. Таке кодування називається ефективним, або статистичним.

З метою зменшення статистичної надмірності, обумовленої наявністю статистичної залежності між елементами повідомлення, також застосовується укрупнення елементарних повідомлень. При цьому кодування здійснюється довгими блоками. Імовірнісні зв'язки між блоками менші ніж між окремими елементами повідомлень, і чим довші блоки, тим менша залежність між ними.

Значення укрупнення пояснимо на прикладі буквеного тексту: якщо імовірнісні зв'язки між буквами в будь-якій мові відносно сильні, то між словами вони значно менші, ще менші між фразами, а тим більше між абзацами. Тому кодування цілих слів, фраз, абзаців дозволяє достатньо повно усунути надлишковість, обумовлену імовірнісними зв'язками. Проте при цьому збільшується затримка передачі повідомлень, оскільки спочатку формується блок повідомлення і лише потім виконуються його кодування і передача.

Для зменшення статистичної надмірності, обумовленої нерівноімовірністю повідомлень джерела, використовуються оптимальні нерівномірні коди, в яких завдяки більш раціональній побудові повідомлень вторинного алфавіту досягається значне зменшення надмірності первинного алфавіту.

Ідея побудови оптимальних нерівномірних кодів полягає в тому, що найімовірнішим повідомленням ставляться у відповідність найкоротші кодові комбінації, а найменш імовірним – більш довгі. Проте через нерівномірність таких кодів і їх випадковий характер передача без втрат інформації з постійною швидкістю проходження кодових символів може бути забезпеченою лише за наявності буферного накопичувача з досить великою пам'яттю і, отже, при допустимості великих затримок.