
- •1.1 Предмет курсу. Види інформації. Теорема дискретизації
- •1.2 Базові поняття теорії інформації
- •1.3 Способи вимірювання інформації
- •1. 4 Ентропія джерела. Властивості кількості інформації та ентропії
- •Розв'язання
- •Розв'язання
- •2.1 Умовна ентропія
- •2.2 Модель системи передачі інформації
- •2.3 Види умовної ентропії
- •2.4 Ентропія об'єднання двох джерел інформації
- •2.5 Продуктивність дискретного джерела інформації. Швидкість передачі інформації
- •2.6 Інформаційні втрати при передачі інформації по дискретному каналу зв'язку
- •2.7 Пропускна здатність дискретного каналу. Основна теорема про кодування дискретного джерела
- •Розв'язання
- •Розв'язання
- •3.1 Способи задання кодів. Статистичне кодування
- •3.2 Елементи теорії префіксних множин
- •3.3 Оптимальні методи статистичного стиснення інформації Шеннона-Фано і Хаффмена
- •Розв'язання
- •I Метод Шеннона-Фано:
- •II Метод Хаффмена:
- •4.1 Теоретичні границі стиснення інформації
- •4.2 Метод блокування повідомлення
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Метод Шеннона-Фано
- •Арифметичний метод
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Розв'язання
Розв'язання
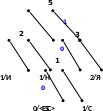
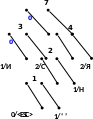
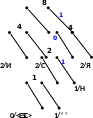
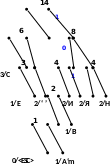
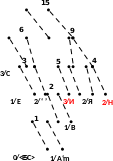
Процес кодування повідомлення і відповідні зміни кодового дерева подаються в табл. 1 і на рис. 1.
Т аблиця
1
аблиця
1
Вхідні дані |
Код |
Довжина Коду |
Номер дерева |
С |
‘C’ |
8 |
1 |
И |
0‘И’ |
9 |
2 |
Н |
00‘Н’ |
10 |
3 |
Я |
100‘Я’ |
11 |
4 |
Я |
001 |
3 |
5 |
|
100‘ ’ |
11 |
6 |
С |
101 |
3 |
7 |
И |
00 |
2 |
8 |
Н |
101 |
3 |
9 |
Е |
1100‘Е’ |
12 |
10 |
В |
11000‘В’ |
13 |
11 |
А |
10100‘А’ |
13 |
12 |
|
1010 |
4 |
13 |
С |
101 |
3 |
14 |
И |
101 |
3 |
15 |
Н |
101 |
3 |
16 |
И |
111 |
3 |
|
2 )
)


3)
4
0/<ESC>



 )
)

5
 )
)


6
 )
7)
)
7)

8)


9)
1

 0)
11)
0)
11)
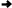


12)
1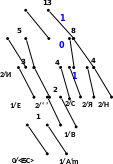
 3)
3)
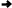

14)

15)


16)
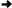
Рисунок 1
Довжина коду стиснутого повідомлення L(X)=114 (бітів).
Довжина ASCII+коду нестиснутого повідомлення L(X)=136(бітів).
Приклад 2 Розпакувати повідомлення ‘B’0‘D’00‘C’11111 110101011011110100101, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжину стиснутого і нестиснутого повідомлення у бітах.
Розв'язання
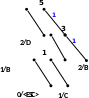
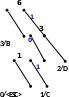
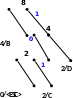
Процес декодування ілюструється таблицею 1, відповідні зміни кодового дерева – рис. 1.
Т аблиця
1
аблиця
1
Вхідний код |
Символ |
Довжина Коду |
Номер дерева |
|
‘B’ |
B |
8 |
1 |
|
0‘D’ |
D |
9 |
2 |
|
00‘C’ |
C |
10 |
3 |
|
11 |
D |
2 |
4 |
|
11 |
B |
2 |
5 |
|
11 |
B |
2 |
6 |
|
101 |
C |
3 |
7 |
|
0 |
B |
1 |
8 |
|
101 |
C |
3 |
9 |
|
101 |
D |
3 |
10 |
|
11 |
C |
2 |
11 |
|
101 |
D |
3 |
12 |
|
0 |
B |
1 |
13 |
|
0 |
B |
1 |
14 |
|
101 |
D |
3 |
|
|
=53 |
|
|||

2)



3) 4)

 5) 6)
5) 6)

7) 8)
9


 )
)


 10) 11)
10) 11)

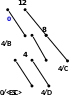

12) 13) 14)
Рисунок 1
Отже, закодоване повідомлення BDCDBBCBCDCDBBD.
Довжина стиснутого повідомлення L(X)=53 (біти).
Довжина нестиснутого повідомлення в коді ASCII+
L(X)=158=120 (бітів).
Задачі до розділу 6
Закодувати повідомлення AABCDAACCCCDBB за адаптивним алгоритмом Хаффмена. Обчислити довжину у бітах стиснутого повідомлення і його ASCII+-коду.
Закодувати повідомлення КИБЕРНЕТИКИ за адаптивним алгоритмом Хаффмена. Обчислити довжини в бітах стиснутого повідомлення і його ASCII+- коду.
Розкодувати повідомлення ‘A’0‘F’00‘X’01111101010110111101 00101, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.
Розкодувати повідомлення ‘D’0‘B’0100‘C’000‘A’11010 11111110, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.
Закодувати повідомлення МАТЕМАТИКА за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.
Розкодувати повідомлення ‘B’0‘D’00‘C’01111101010110111101 00101, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.
Розкодувати повідомлення ‘К’0‘Р’00‘А’100‘С’000‘Н’011100‘Я’ 0100‘ ’1100101001011110, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.
Закодувати повідомлення ПРОГРАММА за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.
Закодувати повідомлення ТЕОРИЯ ИНФОРМАЦИИ за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.
Розкодувати повідомлення ‘В’0‘О’00‘ ’100‘Д’1010000‘Р’0100‘Е’ 01011001010010000‘Н’10000‘И’111100‘К’, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.
Розкодувати повідомлення ‘X’0‘F’00‘Z’1111101100‘A’11101011, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.
1 Шеннон К. Работы по теории информации и кибернетике. - М., Изд-во иностранной литературы, 1963.
2 Фано Р. Передача інформації. Статистична теорія зв'язку. –М.:
Мир, 1965.
