3.2 Елементи теорії префіксних множин

Префіксною множиною S називається скінченна множина двійкових слів, в якій жодна з послідовностей не є префіксом (початком) ніякої іншої.

Якщо S={w₁, w₂, …, w_k} – префіксна множина, то можна визначити вектор (S)=(L₁, L₂, …, L_k), що складається із значень довжин відповідних префіксних послідовностей у неспадному порядку. Цей вектор називається вектором Крафта, для якого виконується нерівність Крафта:

. (2.1)

Для вектора Крафта справедливе таке твердження: якщо S - префіксна множина, то (S) - вектор Крафта.

Якщо нерівність (2.1) переходить в строгу рівність, то такий код називається компактним і має найменшу серед кодів з даним алфавітом довжину, тобто є оптимальним.

Приклади префіксних множин і відповідних їм векторів Крафта: S1={0, 10, 11} (S1)=(1, 2, 2); S2={0, 10, 110, 111} (S2)=(1, 2, 3, 3); S3={0, 10, 110, 1110, 1111} (S3)=(1, 2, 3, 4, 4); S4={0, 10, 1100, 1101, 1110, 1111} (S4)={1, 2, 4, 4, 4, 4}; S5={0, 10, 1100, 1101, 1110, 11110, 11111} (S5)=(1, 2, 4, 4, 4, 5, 5); S6={0, 10, 1100, 1101, 1110, 11110, 111110, 111111} (S6)=(1, 2, 4, 4, 4, 5, 6, 6).

Припустимо, використовується код без пам'яті для стиснення вектора даних x=(x₁, x₂, …, x_n) з алфавітом А об'ємом k символів.

Позначимо через F=(F₁, F₂, …, F_k) вектор частот символів алфавіту А в повідомленні X.

Кодування повідомлення кодом без пам'яті здійснюється у такий спосіб:

1. складається список символів алфавіту A: a₁, a₂, …, a_k у порядку спадання їх частот появи в X;

2. кожному символу а_j призначається кодове слово w_j з префіксної множини S двійкових послідовностей, для якої вектор Крафта (S)=(L₁, L₂, …, L_k);

3. виходом кодера є об'єднання в одну послідовність усіх отриманих кодових слів.

Тоді довжина кодової послідовності на виході кодера джерела інформації становить

L(X)=LF=L₁F₁+ L₂F₂+…+ L_kF_k. (2.2)

Оптимальним є префіксний код, для якого добуток LF мінімальний: LF min.

3.3 Оптимальні методи статистичного стиснення інформації Шеннона-Фано і Хаффмена

До оптимальних методів статистичного кодування повідомлень належать алгоритми Шеннона-Фано і Хаффмана. Ці алгоритми є найпростішими методами стиснення інформації і належать до так званих кодів без пам'яті, що не враховують значення попередніх символів.

Розглянемо алгоритми побудови оптимальних кодів Шеннона-Фано і Хаффмена.

Метод Шеннона-Фано. Значення д. в. в. розміщуються у порядку спадання ймовірностей. Потім уся сукупність розділяється на дві приблизно рівні за сумою ймовірностей частини: до коду першої частини додається 0, а до коду другої - 1. Кожна з частин за тим самим принципом знову розділяється (якщо це можливо) на дві частини і т.д.

Приклад 3 Побудуємо таблицю кодів за методом Шеннона-Фано для повідомлень, заданих розподілом ймовірностей (табл. 2.2).

Таблиця кодів подається у табл. 2.3.

Таблиця 2.3

Буква, хi	Імовір-ність, pi	Код								Довжина коду, li		pili
А	0,6	1							1		0,6
Б	0,2	0	1						2		0,4
В	0,1	0	0	1					3		0,3
Г	0,04	0	0	0	1				4		0,16
Д	0,025	0	0	0	0	1			5		0,125
Е	0,015	0	0	0	0	0	1		6		0,09
Ж	0,01	0	0	0	0	0	0	1	7		0,07
З	0,01	0	0	0	0	0	0	0	7		0,07
pi=1		pili=1,815

Середня довжина коду (біт/сим).

Надлишковість коду , тобто на порядок менше, ніж для рівномірного кодування (приклад 1).

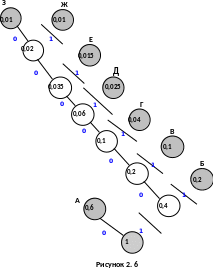
Метод Хаффмана. Код будується за допомогою бінарного дерева. Ймовірності д. в. в. розміщуються у спадному порядку і приписуються листю кодового дерева. Величина, що приписується вузлу дерева, називається його вагою. Два листи або вузли з найменшими значеннями ваги утворюють батьківський вузол, вага якого дорівнює сумарній вазі вузлів, що його складають. Надалі цей вузол враховується нарівні з вершинами, що залишилися, а листя або вузли, що його утворили, більше не розглядаються. Після побудови кореня кожна визначена гілка, що виходить з батьківського вузла, позначається 0 (як правило, якщо це ліва гілка) або 1 (права гілка). Коди значень д. в. в. – це послідовності 0 і 1, що утворюються, на шляху від кореня кодового дерева до листа із заданою імовірністю д. в. в.

Приклад 4 Побудуємо таблицю кодів за алгоритмом Хаффмена для повідомлень, заданих табл. 2.2.

Кодове дерево і таблиця кодів наведені на рис. 2.6 і в табл.2.4 .

Таблиця 2.4

Буква, xi	Ймовір- ність, рi		Код, Code(Хi)	Довжина коду, li	lipi
А	0,6		0	1	0,6
Б	0,2		1 1	2	0,4
В	0,1		1 0 1	3	0,3
Г	0,04		1 0 0 1	4	0,16
Д	0,025		1 0 0 0 1	5	0,125
Е	0,015		1 0 0 0 0 1	6	0,09
Ж	0,01		1 0 0 0 0 0 1	7	0,07
З	0,01		1 0 0 0 0 0 0	7	0,07
pi=1		pili=1,815

Середня довжина коду (біт/сим).

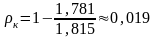Надлишковість коду , тобто істотно менше, ніж для примітивного рівномірного коду.

Звернемо увагу, що для кодів Хаффмена і Шеннона-Фано середня кількість бітів на одне елементарне повідомлення х_i наближається до ентропії джерела Н(Х), але не може бути менше. Такий висновок є наслідком теореми кодування джерела у відсутності шуму³:

Будь-яке джерело дискретних повідомлень можна закодувати двійковою послідовністю з середньою кількістю двійкових символів (бітів) на одне елементарне повідомлення, скільки завгодно близькою до ентропії джерела Н(Х), і неможливо досягти середньої довжини коду, меншої за Н(Х).

Недоліки алгоритмів Шеннона-Фано і Хаффмена:

1 Необхідність побудови таблиці ймовірностей для кожного типу даних, що стискаються. Цей недолік неістотний, якщо стисненню підлягає російський або англійський текст. Проте в загальному випадку, коли імовірність символів невідома, ці алгоритми реалізуються в два проходи: у перший здійснюється збирання частот символів, оцінка їхніх ймовірностей і складання таблиці кодів, другий - використовується саме для стиснення.

2 Необхідність зберігання (передачі) таблиці кодів разом із стисненим повідомленням, що знижує ефект стиснення.

3 Мінімальна довжина кодових слів не може бути менше одиниці, тоді як ентропія повідомлень може бути близькою до нуля. У цьому випадку оптимальні методи кодування виявляються істотно надмірними. Цей недолік долається використанням алгоритму до блоків символів, але при цьому ускладнюється процедура кодування/ декодування і значно розширюється таблиця кодів.

4 Найкращий ефект стиснення досягається тільки у випадку, коли імовірності символів є цілими від'ємними степенями двійки, тобто 1/2, 1/4, 1/8, 1/16 і т.д. На практиці такі ситуації досить рідкі або можуть бути штучно створені розбиттям повідомлень на блоки різної довжини і кодуванням цих блоків, розглядаючи їх як одиниці повідомлення, що викликає відповідне ускладнення алгоритму.

Зразки розв'язування задач до розділу 3

Приклад 1 Для ансамблю повідомлень, заданого таким розподілом ймовірностей: 0,18; 0,17; 0,16; 0,15; 0,1; 0,08; 0,05; 0,05; 0,04; 0,02, побудувати двійкові коди Шеннона-Фано і Хаффмена. Визначити основні характеристики кодів.