3.1 Способи задання кодів. Статистичне кодування

Кодування інформації, здійснюване для зменшення надмірності повідомлень, називається економним кодуванням, або стисненням інформації.

Мета стиснення - зменшення кількості бітів, необхідних для зберігання і передачі інформації, що надає можливість передавати повідомлення швидше і зберігати економніше і оперативніше.

Розглянемо приклади кодів і способи їх задання.

Найпростішим способом представлення кодів є кодові таблиці, що зіставляють символам повідомлень певні кодові комбінації. Приклад кодової таблиці подається в табл. 2.1.

Неважко переконатися, що будь-яке повідомлення x_i з алфавіту об'ємом k можна закодувати послідовністю кодових символів з набору розміром N=q^l комбінацій, де Nk, l - довжина кодової комбінації. У загальному випадку . Наприклад: k=32, q=2, тоді l=5, відповідними двійковими кодовими комбінаціями будуть 00000…11111; k=1000, q=10, тоді l=3, кодові комбінації – 0…999.

Основа коду q може бути довільною, проте в комп'ютерних системах передачі і зберігання інформації найбільш поширені двійкові (бінарні) коди.

Таблиця 2.1

Символ xi	Число	Код з основою 10	Код з основою 4	Код з основою 2
А	0	0	00	000
Б	1	1	01	001
В	2	2	02	010
Г	3	3	03	011
Д	4	4	10	100
Е	5	5	11	101
Ж	6	6	12	110
З	7	7	13	111

Наочним і зручним способом задання кодів є їхнє подання у вигляді кодового дерева (рис. 2.1).

Рисунок 2. 1

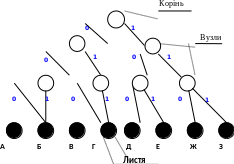
Для цього, починаючи з деякої точки - кореня кодового дерева, проводяться гілки, що позначаються 0 або 1. На листях кодового дерева знаходяться символи алфавіту джерела, причому кожному символу відповідає свій лист і свій шлях від кореня до відповідного листа, який утворює певну кодову комбінацію.

Код, поданий кодовим деревом на рис. 2.1, є примітивним рівномірним трирозрядним кодом. Перевага рівномірних кодів, що мають однакову для всіх символів довжину, полягає в простоті кодування/декодування і синхронізації системи (рис. 2.2).

Прикладом нерівномірного коду може бути кодове дерево, зображене на рис. 2.3.

Рисунок 2. 2

Це приклад непрефіксних кодів. На практиці такі коди не можуть застосовуватися без спеціальних роздільників.

Найбільш поширені нерівномірні коди, що однозначно декодуються. Для цього необхідно, щоб всім символам алфавіту відповідали листя кодового дерева (рис. 2.4), причому жодна кодова комбінація не повинна бути початком (префіксом) іншої, більш довгої, - це префіксні коди.

Задача прийому і декодування нерівномірних кодів набагато складніша, оскільки надходження елементів повідомлення стає неперіодичним (рис.2.5).

Розглянемо приклади кодування повідомлень x_i з алфавіту об'ємом k=8 за допомогою l-розрядного двійкового коду.

Приклад 1 Нехай джерело видає одне з 8 повідомлень А...З, що мають однакову імовірність.

Кодування цих повідомлень рівномірним трирозрядним кодом наведено в табл. 2.1. Тоді:

- ентропія джерела  (біт/сим);

- надлишковість джерела ;

- середня довжина коду (біт/сим);

- надлишковість коду .

Отже, при передачі рівноімовірних повідомлень надлишковість рівномірного коду дорівнює нулю, тобто в цьому випадку рівномірне кодування є оптимальним.

Приклад 2 Припустимо, що повідомлення нерівноймовірні (табл. 2.2).

Таблиця 2.2

А	Б	В	Г	Д	Е	Ж	З
0,6	0,2	0,1	0,04	0,025	0,015	0,01	0,01

Ентропія джерела при цьому буде менше: Н(Х)1,781 (біт/сим).

Середнє число символів на одне повідомлення при використовуванні рівномірного трирозрядного коду (біт/сим).

Надлишковість коду , тобто має досить велику величину (в середньому 3 символи з 10 не несуть ніякої інформації).

Отже, при кодуванні нерівноімовірних повідомлень рівномірні коди характеризуються значною надмірністю. У таких випадках доцільно використовувати нерівномірні коди, довжина кодових комбінацій яких залежить від імовірності символів в повідомленні. Таке кодування називається статистичним. Нерівномірний код при статистичному кодуванні вибирається так, щоб більш імовірні значення передавалися за допомогою більш коротких комбінацій коду, а менш імовірні - за допомогою більш довгих. У результаті зменшується середня довжина коду.