7. Методы безусловной минимизации выпуклых функций многих переменных (метод покоординатного спуска, метод градиентного спуска, метод наискорейшего спуска).

Метод покоординатного спуска.

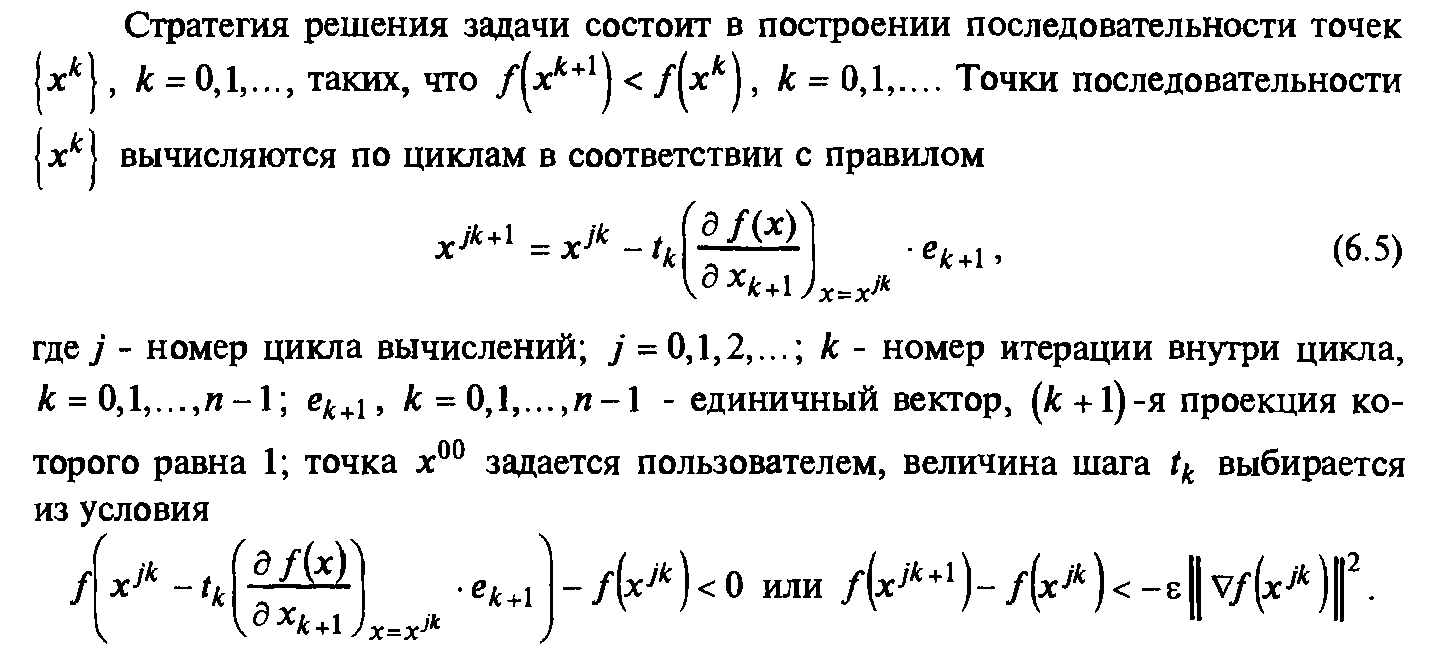
Метод градиентного спуска.

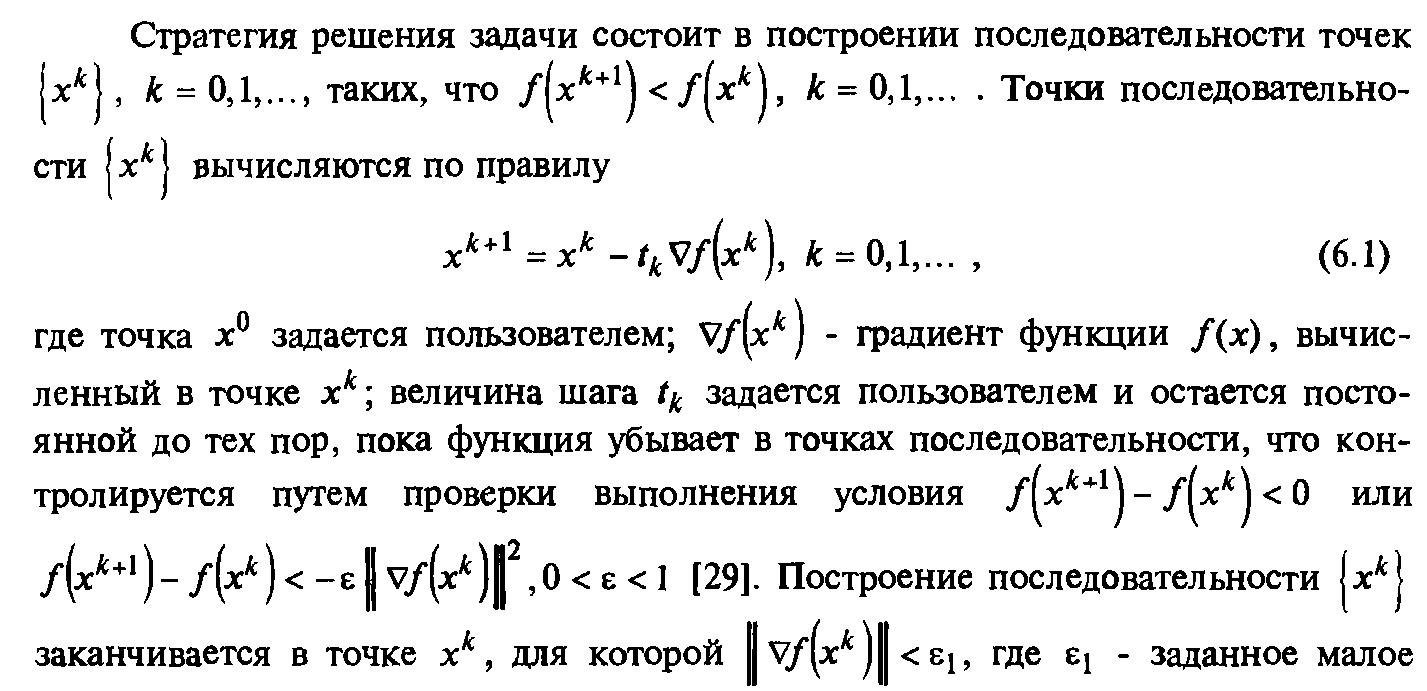
Метод наискорейшего спуска.

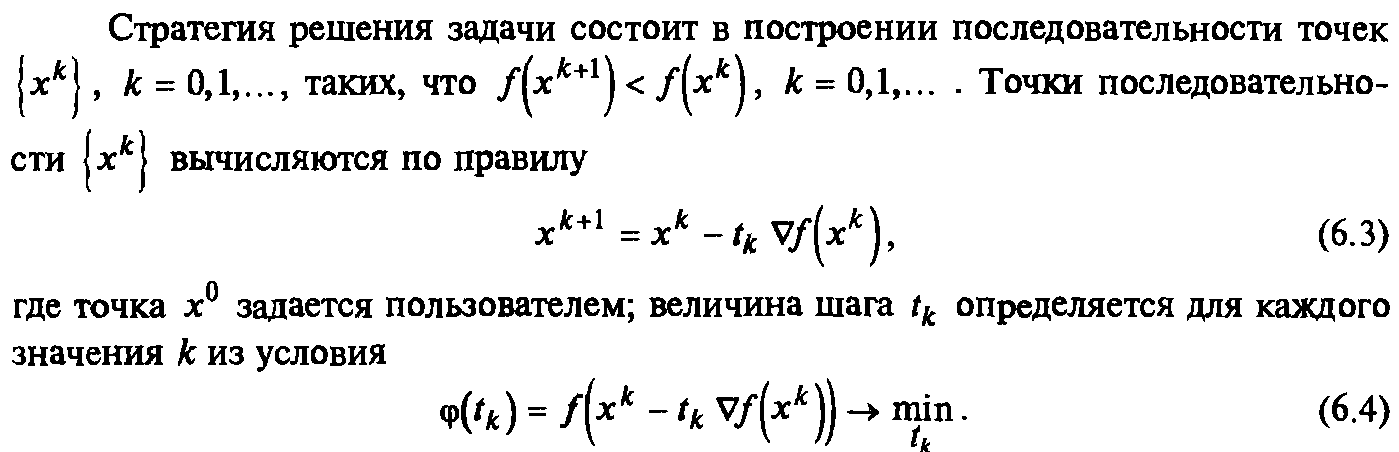
8. Методы штрафных функций.

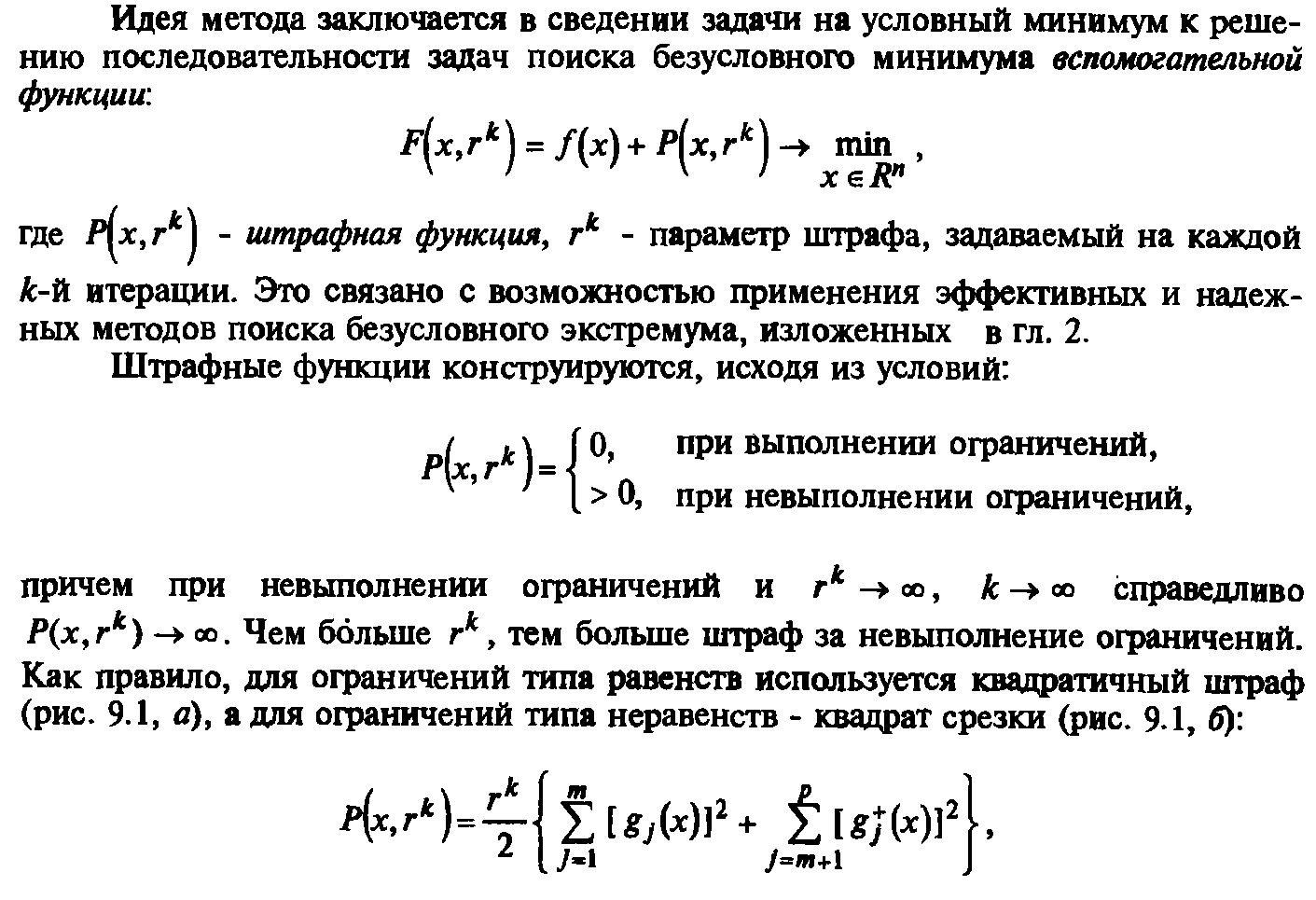
9. Постановка задачи линейного программирования (лп). Эквивалентные формы задач лп. Приведение задачи лп к каноническому виду.

Задача ЛП имеет вид:

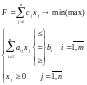(1)

Если в ограничениях с b_i стоят только неравенства, то говорят, что задача задана в стандартной форме.

Если стоят только равенства, то в канонической форме.

Канонический вид всегда можно получить из стандартной определенными способами (добавление / вычитание дополнительных переменных).

Система уравнений в (2) в случае ее совместности и ранга = m имеет некоторый базис, содержащий m векторов, через которые можно выразить  другой вектор A_i, составленный из коэффициентов a_ij.

Переменные x_i, соответствующие базисным векторам, называются базисными, остальные (n – m) переменных – свободными.

Базисным решением m линейных уравнений с n переменными называется решение, в котором все свободные = 0, если при этом все x_i  0, то базисное решение называется допустимым

Допустимое базисное решение – решение, в котором все свободные = 0, а базисные равны свободным элементам.

Каждому допустимому базисному решению соответствует одно угловая точка. Поэтому для того чтобы найти первую угловую точку надо уметь находить некоторое допустимое базисное решение.

Ограничение имеет предпочтительный вид, если левая часть ограничения содержит переменную с коэффициентом 1, которая в остальные ограничения вводится коэффициентом 0.

Если каждые ограничения имеют предпочтительный вид, то система ограничений называется предпочтительной.

В этом случае базисные решения находит так: приравниваем к 0 непредпочтительные переменные, тогда предпочтительные переменные будут равны соответствующим значениям правой части, которой по определению 0. Таким образом, получаем допустимое базисное решение. Предпочтительные переменные будут базисными, а непредпочтительные – свободными.

10. Геометрическая интерпретация задачи лп. Графический метод решения задач лп.

Графический способ решения задачи ЛП состоит из трех этапов:

1. Построение пространства допустимых решений, удовлетворяющих всем ограничениям модели.

2. Построение линий уровня целевой функции.

3. Нахождение оптимального решения среди всех точек пространства допустимых решений.

особенности задач ЛП:

• допустимое множество есть выпуклый многоугольник (результат пересечения полуплоскостей – выпуклых множеств), в трёхмерном пространстве – выпуклый многогранник (подробнее о выпуклых множествах – в следующем пункте);

• допустимое множество является замкнутым (но не обязательно ограниченным);

• наибольшее (или наименьшее) значение целевой функции достигается на границе допустимого множества (в вершине или на грани).

Решение задачи линейного программирования графическим методом включает следующие этапы:

1. На плоскости X₁0X₂ строят прямые.

2. Определяются полуплоскости.

3. Определяют многоугольник решений;

4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;

5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.

6. Вычисляют координаты точки и значение целевой функции в этой точке.