
- •Теорія інформації
- •Тулякова н.О.0 теорія інформації
- •Теорія інформації
- •1.1 Предмет курсу. Види інформації. Теорема дискретизації
- •1.2 Базові поняття теорії інформації
- •1.3 Способи вимірювання інформації
- •1. 4 Ентропія джерела. Властивості кількості інформації та ентропії
- •Розв'язання
- •Розв'язання
- •2.1 Умовна ентропія
- •2.2 Модель системи передачі інформації
- •2.3 Види умовної ентропії
- •2.4 Ентропія об'єднання двох джерел інформації
- •2.5 Продуктивність дискретного джерела інформації. Швидкість передачі інформації
- •2.6 Інформаційні втрати при передачі інформації по дискретному каналу зв'язку
- •2.7 Пропускна здатність дискретного каналу. Основна теорема про кодування дискретного джерела
- •Розв'язання
- •Розв'язання
- •3.1 Способи задання кодів. Статистичне кодування
- •3.2 Елементи теорії префіксних множин
- •3.3 Оптимальні методи статистичного стиснення інформації Шеннона-Фано і Хаффмена
- •Розв'язання
- •I Метод Шеннона-Фано:
- •II Метод Хаффмена:
- •4.1 Теоретичні границі стиснення інформації
- •4.2 Метод блокування повідомлення
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Метод Шеннона-Фано
- •Арифметичний метод
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •7.1 Алгоритм lz77
- •7.2 Алгоритм lzss
- •7.3 Алгоритм lz78
- •7.4 Алгоритм lzw
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •8.1 Огляд типів систем стиснення інформації
- •8.2 Стиснення без втрат інформації
- •8.3 Стиснення із втратами інформації
- •9.1 Основні принципи
- •9.2 Елементи двійкової арифметики
- •9.3 Код з перевіркою на парність
- •9.4 Ітеративний код
- •Розв'язання
- •Розв'язання
- •10.1 Способи задання лінійних кодів. Твірна матриця лінійного блокового коду
- •10.2 Перевірна матриця лінійного блокового коду
- •10.3 Кодовий синдром і виявлення помилок лінійним блоковим кодом
- •10.4 Синдромне декодування лінійних блокових кодів
- •10.5 Вага і відстань Хеммінга. Можливості лінійних кодів виявляти і виправляти помилки
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •12.1 Операції над поліномами в полі двійкових символів gf(2)
- •12.2 Поліноміальні коди
- •12.3 Циклічні коди
- •12.4 Синдром і виправлення помилок у циклічних кодах
- •12.5 Твірна і перевірна матриці циклічного коду
- •12.6 Способи декодування циклічного коду
- •Розв'язання
- •Розв'язання
- •Розв'язання
Розв'язання
Синдром виправлення поодиноких помилок циклічним кодом визначається діленням многочлена вектора помилок на твірний поліном коду.
Припустимо, що кодується повідомлення m довжиною k символів – йому відповідає многочлен m(x) степеня k-1.
Кодовим словом на виході кодера буде послідовність u довжиною n символів, якій відповідає многочлен u(x) степеня n-1.
Позначимо через e= (e0, e1, …, en-1) – вектор помилок в двійковому каналі зв'язку; s=(s0, s1, …, sn-k-1) – кодовий синдром, що визначається вектором помилок.
Вектор помилок подається многочленом вигляду e(x)=e0+e1x+…+en-1xn-1, а синдром – многочленом s(x)=s0+s1x+…+sn-k-1xn-k-1.
Знайдемо значення синдрому виправлення поодиноких помилок заданим циклічним (4, 7)- кодом:
е=(1000000) e(x)=1,
1 x3 +x +1
s(x)= 1 (100);
е=(0100000) e(x)=x,
 x
x3
+x
+1
x
x3
+x
+1
s(x)= x (010);
е=(0010000) e(x)=x2,
 x2
x3
+x
+1
x2
x3
+x
+1
s(x)= x2 (001);
e=(0001000) e(x)=x3,
x 3
x3
+x
+1
3
x3
+x
+1
+ x3 + x+ 1 1
x + 1
s(x)= 1+ x (110);
e=(0000100) e(x)=x4,
x 4
x3
+x
+1
4
x3
+x
+1
+ x4 +x2 +x x
x2 + x
s(x)= x + x2 (011);
e=(0000010) e(x)=x5,
 x5
x3
+ x
+1
x5
x3
+ x
+1
+ x5 +x3 +x2 x2 +1
x3+ x2
+ x3+ x+ 1
x2+ x + 1
s(x)= 1+x+x2 (111);
e=(0000001) e(x)=x6,
x 6 x3 + x + 1
+x6 +x4 +x3 x3+ x + 1
x4 + x3
+ x4 + x2 + x
x3 + x2 +x
+x3 + x + 1
x2 + 1
s(x)= 1+x2 (101).
Знайдені комбінації синдрому є стовпцями перевірної матриці:
![]()
 .
.
Одинична
підматриця
I(n-k)×(n-k)
Транспонована
перевірна частина P(n-k)×k
твірної
матриці коду
З перевірної матриці знаходимо твірну матрицю коду
![]()
 .
.
Перевірна
частина Pk×(n-k)
Одинична
підматриця
Ik×k
Кодове слово утворюється послідовністю u=(0, 1, 2, m0, m1, m2,m3), де 0, 1, 2 – перевірочні символи.
Декодуємо задане повідомлення y=(1001110).
Даній послідовності відповідає поліном
y(x)=1x0+ 0x1+ 0x2+ 1x3+ 1x4+ 1x5+ 0x6=1+x3+ x4+ x5.
Скористаємося алгоритмом декодування циклічних кодів:
З
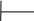 найдемо
остачу від ділення многочлена прийнятої
комбінації на твірний поліном коду і
тим самим перевіримо її на наявність
помилки:
найдемо
остачу від ділення многочлена прийнятої
комбінації на твірний поліном коду і
тим самим перевіримо її на наявність
помилки:
x5+ x4+ x3+ 1 x3 +x +1
+ x5+ x3+ x2 x2 +x
x4+ x2+ 1
+ x4+ x2+ x
x+ 1
s(x)= 1+ x (110).
Ненульова остача s(x) свідчить про наявність помилки в прийнятій комбінації.
Вага остачі (110)= 2 > l, де l= 1 – кратність помилок, що виправляються кодом, отже, необхідно виконати циклічний зсув кодованої послідовності на 1 розряд вправо:
(1001110) (0100111) y(x)=0x0+ 1x1+ 0x2+ 0x3+
+1x4+ 1x5+ 1x6= x+ x4+ x5+ x6.
Розділимо отриманий у результаті циклічного зсуву многочлен на твірний поліном коду:
 x6+
x5+
x4+
x x3
+x
+1
x6+
x5+
x4+
x x3
+x
+1
+x6+ x4+ x3 x3 +x2
x5 + x3 + x
+x5+ x3+ x2
x2 +x
s(x)= x+ x2 (011).
Вага остачі (011)= 2 > 1, отже, виконуємо циклічний зсув кодованої послідовності на 1 розряд вправо:
(0100111) (1010011) y(x)=1x0 +0x1+1x2+ 0x3 + + 0x4+ 1x5+ 1x6= 1+ x2+ x5 + x6.
Розділимо отриманий у результаті циклічного зсуву многочлен на твірний поліном коду:
 x6+
x5+
x2+
1 x3
+x
+1
x6+
x5+
x2+
1 x3
+x
+1
+x6+ x4+ x3 x3 +x2+x
x5+ x4+ x3+ x2+ 1
+x5+ x3+ x2
x4+ 1
+x4+ x2+ x
x2+ x+ 1
s(x)= 1+ x+ x2 (111).
Вага остачі (111)= 3 > 1, знову виконуємо циклічний зсув кодованої послідовності й ділення її многочлена на твірний поліном коду: (1010011) (1101001)
y(x)=1x0+ 1x1+ 0x2+ 1x3+ 0x4+ 0x5+ 1x6= 1+ x+ x3+ x6.
Розділимо многочлен циклічно зсуненої послідовності на твірний поліном коду:
 x6
+
x3+
x+
1 x3+
x+
1
x6
+
x3+
x+
1 x3+
x+
1
+ x6+ x4 + x3 x3 +x
x4+ x +1
+ x4+ x2+ x
x2+ 1
s(x)= 1+ x2 (101).
Вага остачі (101)= 2 > 1, виконуємо циклічний зсув й ділення на твірний поліном: (1101001) (1110100) y(x)= 1x0+ 1x1+ 1x2+ 0x3+ 1x4+ 0x5+ 0x6= 1+ x + x2 + x4.
Знову розділимо многочлен послідовності, отриманої у результаті останнього циклічного зсуву, на твірний поліном:
 x4+
x2+
x+1
x3
+x
+1
x4+
x2+
x+1
x3
+x
+1
+ x4 + x2 + x x
1
s(x)=1 (100).
Вага отриманої остачі (100)= 1 1, виконуємо дії з виправлення помилки.
Для цього додаємо до останнього циклічно зсунутого многочлена його остачу від ділення на твірний поліном:
x4+ x2+ x+ 1+ 1 = x+ x2+ x4 (0110100).
Виконуємо циклічний зсув отриманої кодової комбінації у зворотному напрямку на 4 розряди вліво:
(0110100) (1000110).
Одержуємо виправлену кодову комбінацію u=(1000110).
Декодуємо передану послідовність, вилучивши перевірні елементи в лівій частині кодового слова: (1000110)(0110).
Задачі до розділу 12
Поліноміальний код заданий твірним многочленом g(x)=1+x+x5+x7. Закодувати повідомлення 0100, 10001101, 11110.
Поліноміальний (3, 6) - код заданий многочленом вигляду g(x)=1+x2+x3. Побудувати твірну матрицю коду і таблицю декодування з виправленням помилки.
Закодувати циклічним кодом, здатним виправляти поодинокі помилки, комбінацію 011011. Навести приклад виправлення помилки в кодовій комбінації. Визначити надлишковість коду.
Циклічний (11, 15)- код заданий твірним поліномом вигляду g(x)=1+x3+x4. Побудувати твірну матрицю коду. Навести приклад виправлення помилки даним кодом.
Побудувати перевірну матрицю циклічного (11, 15)- коду, заданого твірним поліномом g(x)=1+x+x4. Виправити помилкову комбінацію 010111101011111 (біти пронумеровані зліва направо).
Побудувати перевірну матрицю циклічного (11, 15)- коду, заданого твірним поліномом вигляду g(x)=1+x+x4. Закодувати послідовність 10010111011 (біти пронумеровані зліва направо). Скільки помилок у прийнятій комбінації може виявити і виправити код?
Циклічний (3, 7)- код заданий твірним поліномом вигляду g(x)=1+x+x2+x4. Визначити мінімальну кодову відстань Хеммінга і здатність коду виявляти і виправляти помилки. Знайти ймовірність невиявлення помилки кодом, якщо ймовірність помилкової передачі біта повідомлення в каналі q=10-4.
Циклічний (4, 15)- код заданий твірним поліномом вигляду g(x)=1+x+x2+x3+x5+x7+x8+x11. Закодувати комбінації 1100, 0011. Визначити мінімальну кодову відстань Хеммінга і здатність коду виявляти і виправляти помилки. Знайти ймовірність невиявлення помилки кодом, якщо ймовірність помилки в каналі q=10-2.
Циклічний код заданий твірним поліномом вигляду g(x)=1+x2+x3. Визначити і виправити помилкові комбінації 0111011, 1011010, 0010110 (біти пронумеровані зліва направо).
Циклічний код заданий твірним поліномом вигляду g(x)=1+x+x3. Визначити і виправити помилкові комбінації коду: 0111011, 1011101, 0011010 (біти пронумеровані зліва направо).
Визначити синдром виправлення помилок циклічним (11, 15)- кодом, заданим твірним поліномом g(x)=1+x3+x4. Побудувати перевірну і твірну матриці коду.
Декодувати повідомлення 1101011, 1110011, закодовані циклічним кодом, заданим твірним поліномом g(x)=1+x2+x3+x4, виправивши помилку, якщо вона є (біти пронумеровані зліва направо).
Закодувати циклічним кодом, заданим твірним поліномом вигляду g(x)=1+x+x3+x4, комбінацію m(x)=1+x4+x7. Навести приклад виправлення помилки даним кодом. Визначити його надлишковість.
Закодувати циклічним кодом, здатним виправляти поодинокі помилки, комбінацію 0111. Навести приклад виправлення помилки в кодовій комбінації. Визначити надлишковість коду.
Циклічний (4, 7)- код заданий твірним поліномом вигляду g(x)=1+x+x3. Знайти перевірний поліном коду, за його допомогою закодувати комбінації 011, 110, 101. Навести приклад виправлення помилки отриманим циклічним кодом.
Контрольні запитання до розділів 9-12
Які коди належать до завадостійких? Якими загальними властивостями вони характеризуються?
Для чого в завадостійкі коди вводиться надлишковість?
Які існують класи завадостійких кодів?
Які коди належать до блокових завадостійких кодів? В яких випадках їх доцільно використовувати?
У чому полягає відмінність блокових і згорткових кодів?
Як визначаються операції додавання та множення за модулем 2 у полі двійкових символів GF(2)?
Які коди належать до лінійних блокових кодів? Які коди мають властивість систематичності?
У чому полягає принцип кодування з перевіркою на парність? Яка надлишковість коду? У чому переваги та недоліки кодування?
Який канал передачі інформації описується моделлю двійкового симетричного каналу?
У чому полягає принцип виявлення і виправлення помилок ітеративним кодом? Які переваги та недоліки такого кодування?
Які існують способи задання лінійних блокових кодів? Які основні частини мають кодові слова лінійного блокового коду?
Що таке система перевірних рівнянь лінійного блокового коду?
Що таке твірна матриця лінійного блокового коду? Які її властивості? Яка структура твірної матриці?
Як, скориставшись твірною матрицею, побудувати систему перевірних рівнянь лінійного блокового коду?
Що таке перевірна матриця лінійного блокового коду? Які її властивості? Яка структура перевірної матриці?
Як, скориставшись перевірною матрицею, побудувати систему перевірних рівнянь лінійного блокового коду?
Як визначається вектор помилок у двійковому каналі зв'язку? У чому полягає задача декодування переданого кодового слова?
Що таке кодовий синдром лінійного коду? Як він визначається?
Яку властивість має кодовий синдром прийнятої кодованої послідовності? У яких випадках синдром не дозволяє знайти помилки у переданій послідовності?
Яким чином за допомогою кодового синдрому виявляються та виправляються помилки лінійним блоковим кодом?
Як визначаються вага і відстань Хеммінга для двійкових послідовностей?
Що таке мінімальна кодова відстань Хеммінга лінійного блокового коду? Як вона визначається?
Як записуються необхідна і достатня умови виявлення лінійним блоковим кодом помилок заданої кратності?
Як записуються необхідна і достатня умови виправлення лінійним блоковим кодом помилок заданої кратності?
Які необхідна і достатня умови існування завадостійкого коду?
Як визначається мінімальна кількість перевірних символів для лінійного блокового коду із заданими характеристиками?
Як побудувати твірну матрицю лінійного блокового коду із заданими характеристиками?
Які лінійні блокові коди називаються кодом Хеммінга?
Як знаходиться кількість інформаційних і перевірних символів для коду Хеммінга?
Як утворюються кодові слова коду Хеммінга?
Як складається перевірна матриця коду Хеммінга?
Як виконується декодування коду Хеммінга?
Як складається твірна матриця коду Хеммінга?
У чому полягає принцип поліноміального кодування?
Як визначаються основні арифметичні операції над поліномами в полі двійкових символів GF(2)?
Які коди називаються поліноміальними?
Що таке твірний поліном коду? Які властивості він має?
Яким чином виявляються помилки поліноміальним кодом? В яких випадках помилки залишаються не знайденими?
Як побудувати твірну матрицю поліноміального коду?
Які поліноміальні коди називаються циклічними? Які їх властивості?
У чому полягає алгоритм кодування циклічним кодом?
Що таке перевірний поліном циклічного коду? Які його властивості?
Як визначається поліном синдрому для циклічних кодів?
Як зв'язаний поліном синдрому з поліномом помилок у каналі?
Як побудувати твірну та перевірну матриці циклічного коду?
Як виявляються і виправляються помилки циклічним кодом?
У чому полягає алгоритм декодування циклічного коду на основі прийняття або відхилення гіпотез?
У чому полягає алгоритм декодування циклічних кодів, що використовує послідовний циклічний зсув елементів кодованої послідовності?
Відповіді до задач
Частина I Розділ 1
 (біт/сим),
(біт/сим),
 (біт/сим);
(біт/сим);HX=1,75 (біт/cим),
 (біт/сим),
(біт/сим),
![]() (біт/сим),
(біт/сим),
![]() (біт/сим),
(біт/сим),
![]() (біт/сим);
(біт/сим);
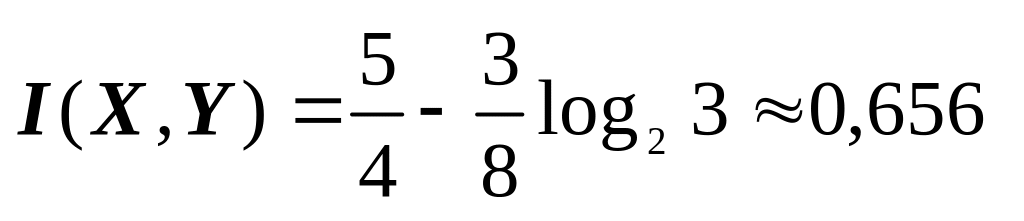 (біт/сим),
HX1=HX2=2 (біт/сим),
(біт/сим),
HX1=HX2=2 (біт/сим),
![]() (біт/сим);
(біт/сим);
I(X, Y)= I(Y, Y)=1 (біт/сим);
I(Z, X1)= I(X1, X1)=HX1=1 (біт/сим); HZ=2 (біт/сим); I(Z, X1)= I(X1, X1) X1 =f(Z);
HX1=1 (біт/сим), HY=1,5 (біт/сим), I(Y, X1)=0,5 (біт/сим);
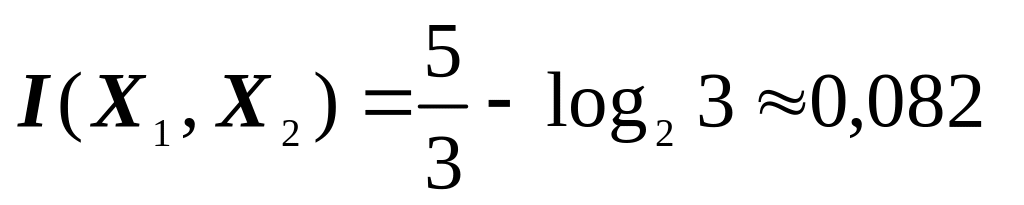 (біт/сим);
(біт/сим);HX=1,75 (біт/сим),
 (біт/сим),
(біт/сим),
 (біт/сим),
I(Z, X)=1,75 (біт/сим),
(біт/сим),
I(Z, X)=1,75 (біт/сим),
 (біт/сим);
(біт/сим);HX=1 (біт/сим),
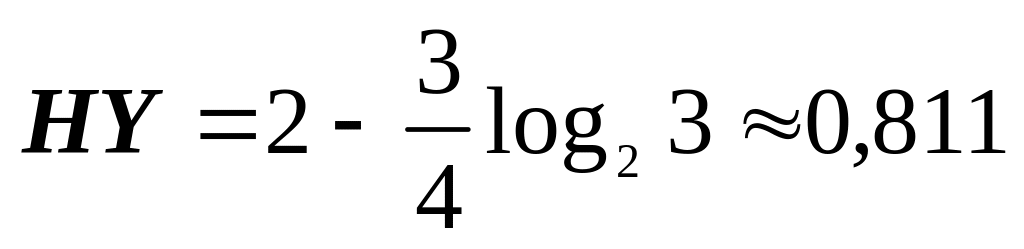 (біт/сим),
(біт/сим),
 (біт/сим);
(біт/сим);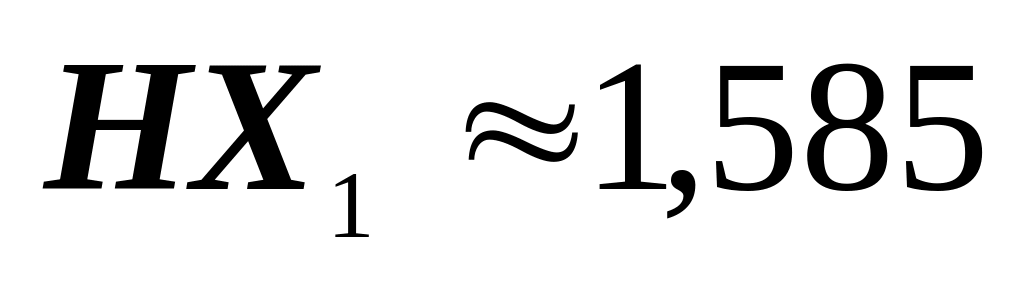 (біт/сим),HX2=1(біт/сим),
(біт/сим),HX2=1(біт/сим),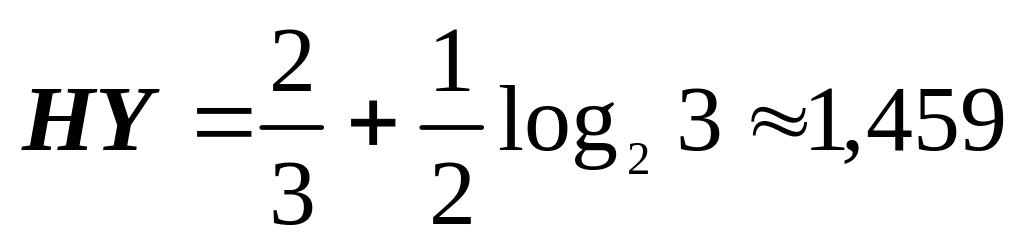 (біт/сим),
(біт/сим), (біт/сим),
(біт/сим), (біт/сим);
(біт/сим);HX=1,5 (біт/сим),
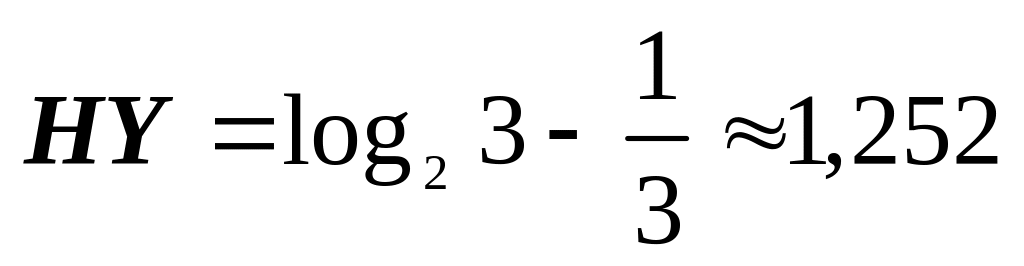 (біт/сим),
(біт/сим),
![]() (біт/сим),
(біт/сим),![]() 1(біт/сим),
1(біт/сим),
![]() (біт/сим);
(біт/сим);
HX=2 (біт/cим), HZ=3,25 (біт/cим), I(Z, X1)=I(Z, X2)=1,25 (біт/cим);
HX=HY=2 (біт/cим), HZ=3,875 (біт/cим), I(Z, X)=1,875 (біт/cим);
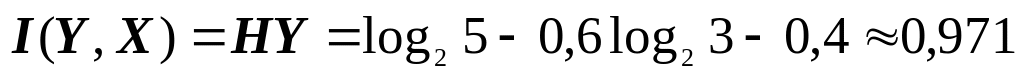 (біт/cим),
(біт/cим), (біт/cим);
(біт/cим);HX=HY=1,75 (біт/cим),
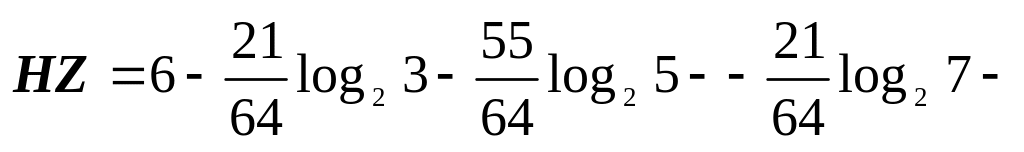
![]() (біт/cим),
(біт/cим),
![]()
![]() (біт/cим),
(біт/cим),![]()
![]() (біт/cим);
(біт/cим);
I(Z, X1)=0 (біт/cим), I(Z, X2)=1 (біт/cим), HX1=HZ=1 (біт/cим);
HX1=HX2=
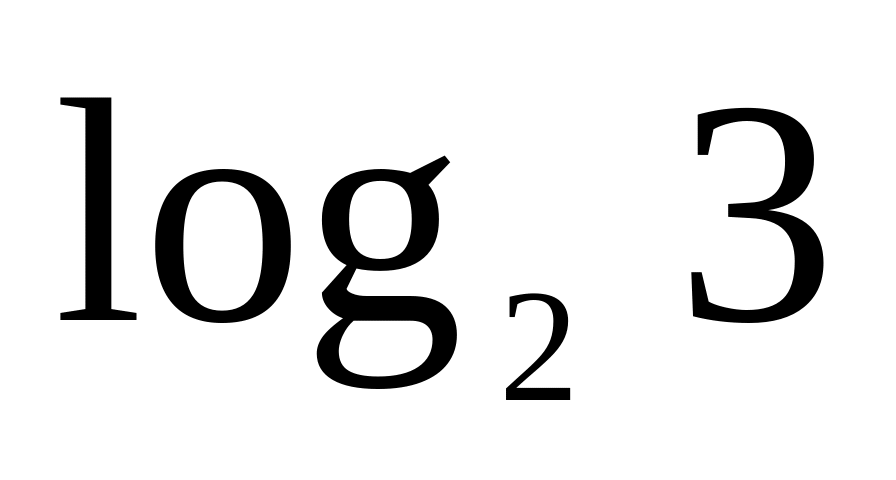 1,585 (біт/сим);
1,585 (біт/сим);
 (біт/сим);
(біт/сим);
 (біт/сим);
(біт/сим); (біт/сим).
(біт/сим).
Частина I Розділ 2
H(Y/x1)0,222 (біт/сим), H(Y/x2)0,705 (біт/сим), H(Y/x3)0,593 (біт/сим), H(Y/X)0,504 (біт/сим), H(X/y1)0,598 (біт/сим), H(X/y2) 0,861 (біт/сим), H(X/y3) 0,184 (біт/сим), H(X/Y)0,467 (біт/сим);
H(X/y1)= 0,954 (біт/сим), H(X/ y2)=0,592 (біт/сим), H(X/y3)=1,522 (біт/сим), H(X/Y)=0,969 (біт/сим), I(X,Y)=0,367 (біт/сим);
H(X/y1)1,116 (біт/сим), H(X/y2)1,485(біт/сим), H(X/y3)1,579 (біт/сим), H(X/y4)1,502 (біт/сим), H(X/Y)1,422 (біт/сим), I(X,Y)0,572 (біт/сим);
H(X/y1)0,244 (біт/сим), H(X/y2)0,336(біт/сим), H(X/y3) 0,161(біт/сим), H(X/Y)0,221 (біт/сим), I(X,Y) 1,264 (біт/сим);
H(X/y1)=0,364 (біт/сим), H(X/y2)=0,974 (біт/сим), H(X/y3)=1,406 (біт/сим), H(X/Y)= 0,621 (біт/сим);
I(X,Y) 0,683 (біт/сим), I(100) 68 (біт), 100H(X/Y)1000,55355 (біт);
H(X/Y)0,216 (біт/сим), C1,37103 (бод), Vи855 (сим/с);
H(X/Y)0,221 (біт/сим), Vк1,26103 (бод);
I(X,Y)0,42 (біт/сим), C434 (бод);
C0,0864 (кбод); безпомилкова передача по каналу неможлива;
H(X/ Y) 0,621 (біт/сим); C964 (бод); безпомилкова передача неможлива.
Частина II Розділ 3
 (біт/сим),
=1;
(біт/сим),
=1;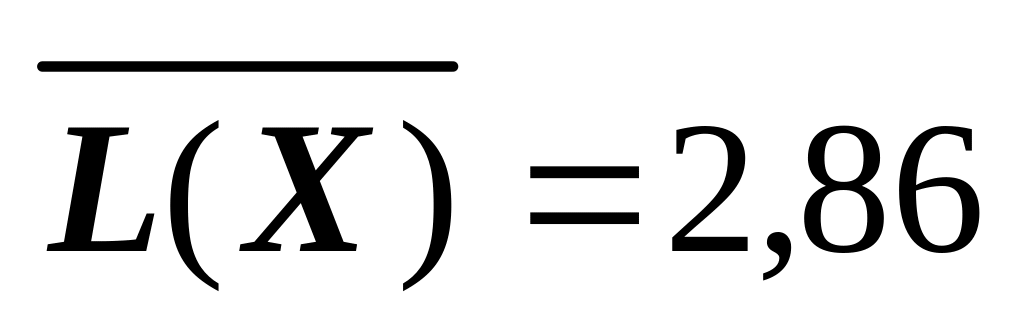 (біт/сим),
к0,02;
(біт/сим),
к0,02;Для коду Шеннона-Фано і коду Хаффмена
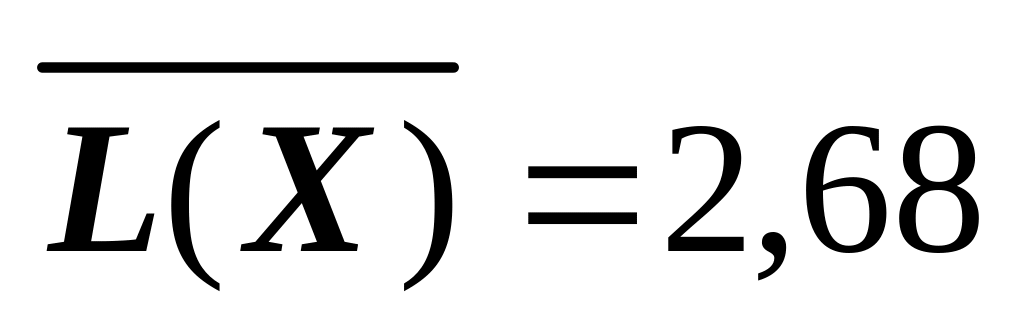 (біт/сим),
надлишковість
коду к0,01;
(біт/сим),
надлишковість
коду к0,01;
HX 2,175 (біт/сим), для коду Шеннона-Фано
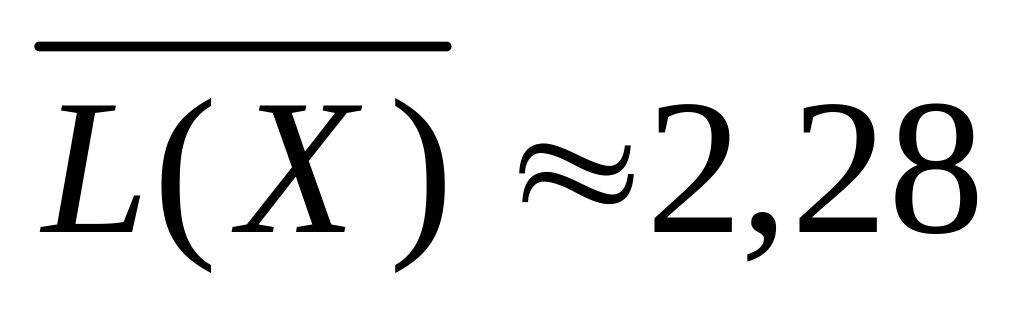 (біт/сим),
для коду
Хаффмена
(біт/сим),
для коду
Хаффмена
 (біт/сим);
(біт/сим);1)
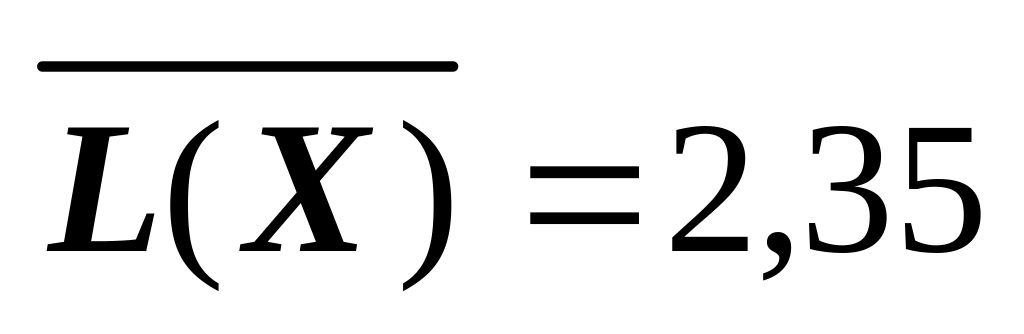 (біт/сим),
2)
(біт/сим),
2) 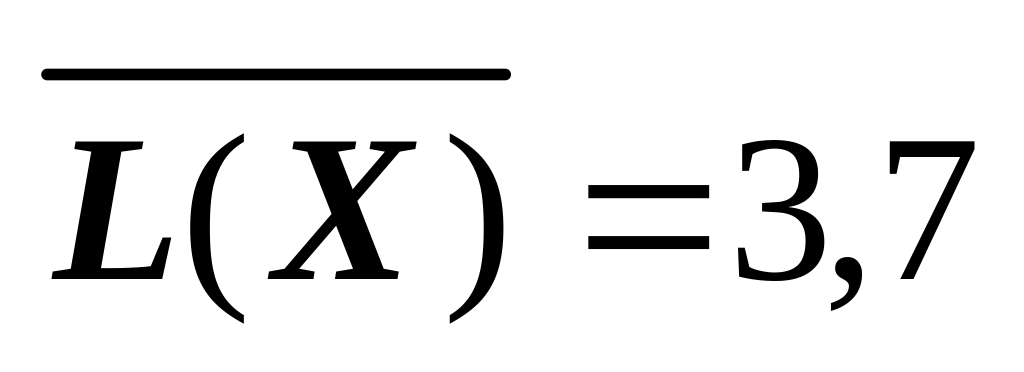 (біт/сим),
3)
(біт/сим),
3)  (біт/сим);
4)
(біт/сим);
4) (біт/сим);
(біт/сим);1)
 (біт/сим),
2)
(біт/сим),
2)  (біт/сим),
3)
(біт/сим),
3) 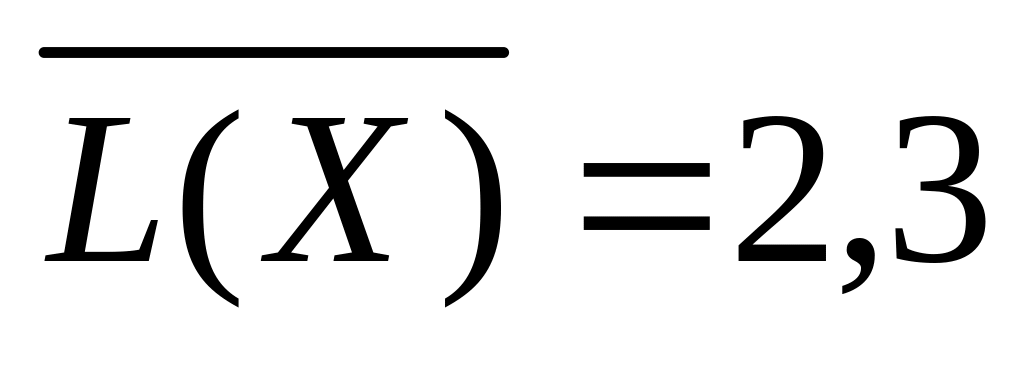 (біт/сим);
(біт/сим);
Частина II Розділ 4
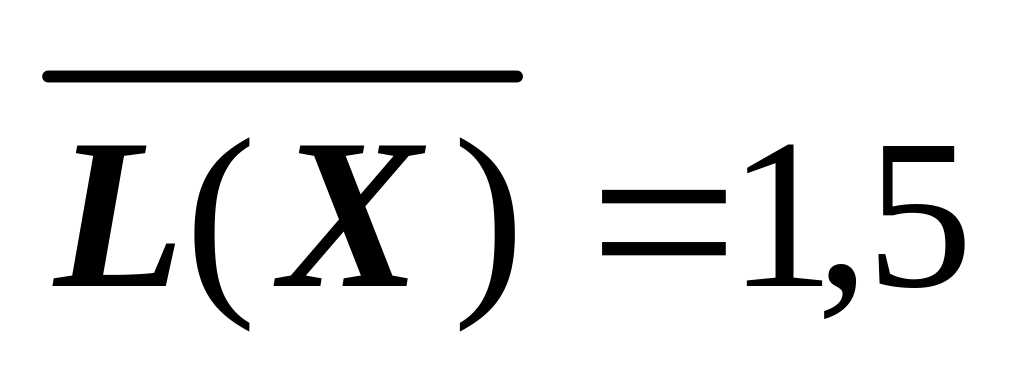 (біт/сим);
(біт/сим);(біт/сим),
 (біт/сим);
(біт/сим);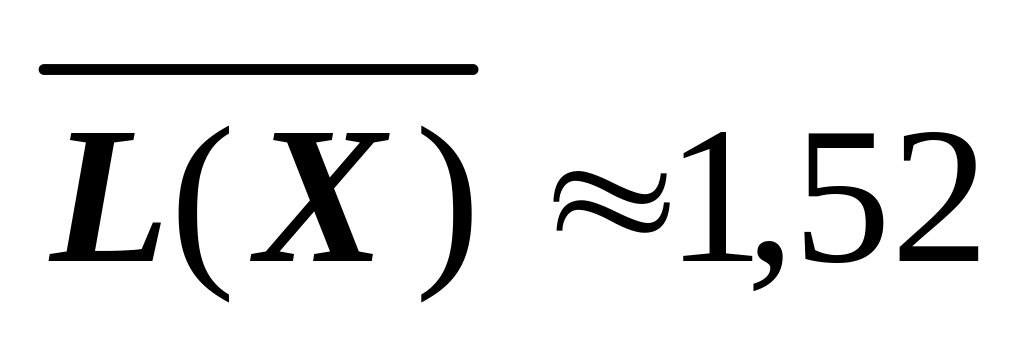 (біт/сим);
(біт/сим);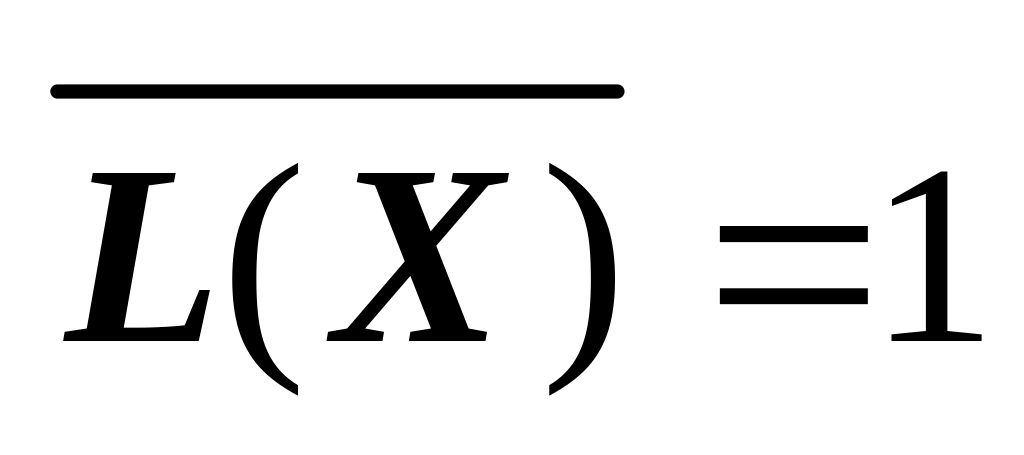 (біт/сим),
(біт/сим),
 (біт/сим),
(біт/сим),
 (біт/сим);
(біт/сим);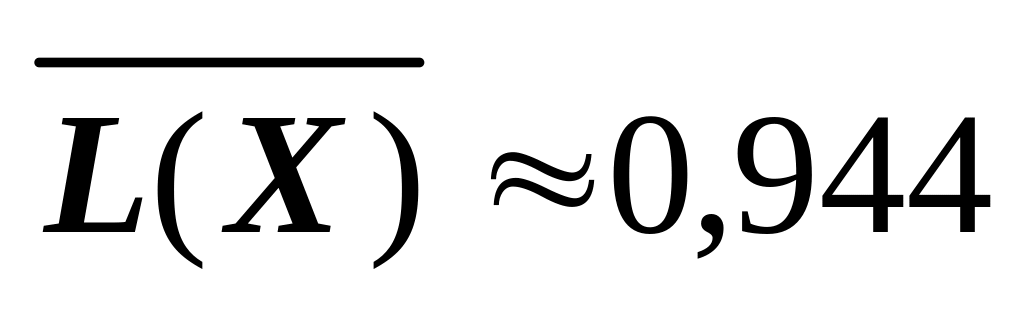 (біт/сим),
(біт/сим),
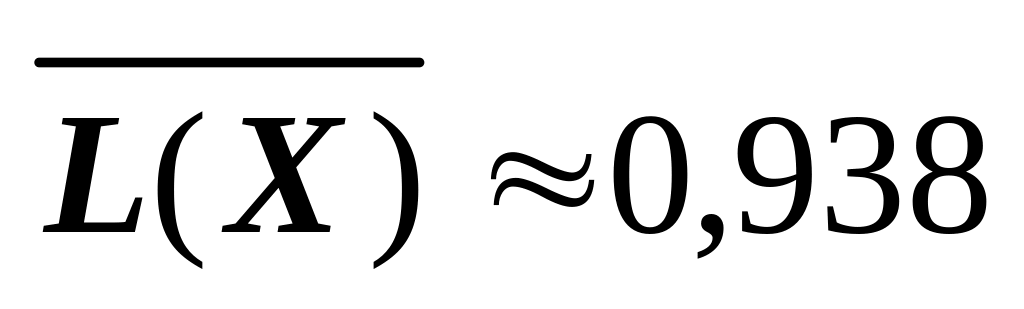 (біт/сим);
(біт/сим);L(X)=7 (біт), R(X)=0,7;
L(X)=13 (біт), L(X)=6 (біт);
L(X)=9 (біт);
Частина II Розділ 5
Шеннона-Фано, Хаффмена (біт/сим), арифметичний
 (біт/сим);
(біт/сим);Шеннона-Фано, Хаффмена
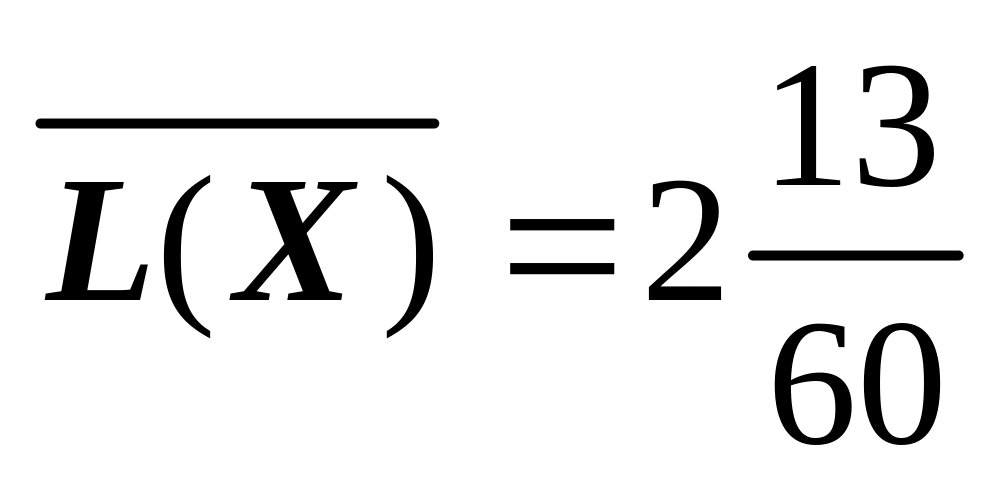 (біт/сим),
арифметичний
(біт/сим),
арифметичний
 (біт/сим);
(біт/сим);Шеннона-Фано, Хаффмена
 (біт/сим),
арифметичний
(біт/сим),
арифметичний
 (біт/сим);
(біт/сим);Шеннона-Фано, Хаффмена (біт/сим), арифметичний
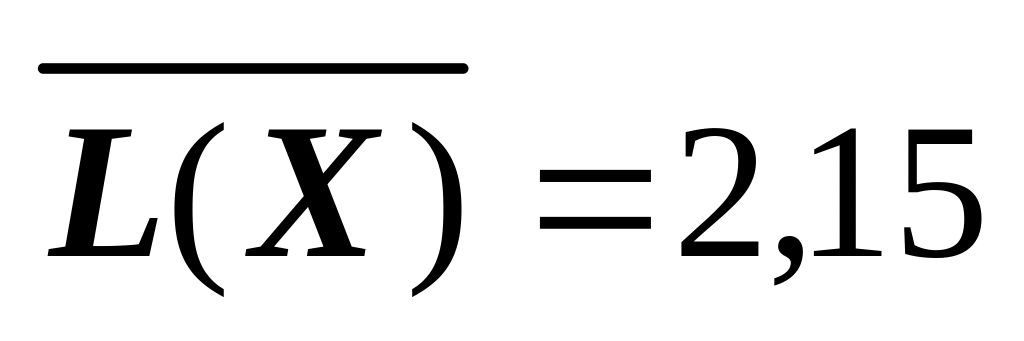 (біт/сим);
(біт/сим);Шеннона-Фано, Хаффмена L(X)=6 (біт), арифметичний L(X)=1 (біт);
L(X)=4 (біт);
L(X)=9 (біт);
BAABCB;
BBABB;
BAABC;
а) 000100; б) 000001; в) 010000;
Частина II Розділ 6
Код повідомлення: ‘A’10‘B’00‘C’000‘D’00011001111100110011001, довжина стиснутого повідомлення Lcode(X)=62 (біт), довжина вхідного коду LASCII+(X)=112 (біт);
Код повідомлення: ‘К’0‘И’00‘Б’100‘Е’000‘Р’1100‘Н’1111000‘Т’1001 10111, довжина стиснутого повідомлення Lcode(X)=85 (біт), нестиснутого - LASCII+(X)=88 (біт);
Закодоване повідомлення AFXAFFXFXAXAFFA, довжина коду стиснутого повідомлення Lcode(X)=52 (біт), довжина ASCII+- коду LASCII+(X)=120 (біт);
Закодоване повідомлення DBBCAABCCB, довжина стиснутого повідомлення Lcode(X)=53 (біт), довжина ASCII+- коду LASCII+(X)=80 (біт);
Код повідомлення: ‘М’0‘А’00‘Т’100‘Е’101001000‘И’0000‘К’10, довжина стиснутого повідомлення Lcode(X)=69 (біт), довжина коду вхідного повідомлення LASCII+(X)=80 (біт);
Закодоване повідомлення: BDCBDDCDCBCBDDB, довжина стиснутого повідомлення Lcode(X)=52 (біт), нестиснутого – LASCII+(X)=120 (біт);
Закодоване повідомлення: КРАСНАЯ КРАСКА, довжина коду стиснутого повідомлення Lcode(X)=91 (біт), нестиснутого – LASCII+(X)=112 (біт);
Код повідомлення: ‘П’0‘Р’00‘О’100‘Г’11000‘А’1000‘М’0101011, довжина стиснутого повідомлення Lcode(X)=70 (біт), довжина коду вхідного повідомлення LASCII+(X)=72 (біт);
Код: ‘Т’0‘Е’00‘О’100‘Р’000‘И’1100‘Я’1000‘ ’1010100‘Н’11100‘Ф’ 10001011000‘М’01100‘А’01000‘Ц’0000, довжина стиснутого повідомлення Lcode(X)=150 (біт), нестиснутого – LASCII+(X)=136 (біт);
Закодоване повідомлення: ВО ДВОРЕ ДВОРНИК, довжина коду стиснутого повідомлення Lcode(X)=117 (біт), нестиснутого – LASCII+(X)=128 (біт);
Закодоване повідомлення: XFZFXZAXFFX, довжина коду стиснутого повідомлення Lcode(X)=53 (біт), нестиснутого – LASCII+(X)=88 (біт);
Частина II Розділ 7
LZ77: <0,0,‘A’> <11,1,‘B’> <0,0,‘C’> <0,0,‘D’> <7,2,‘C’> <11,1,‘C’> <5,2,‘B’> <0,0,‘B’>; Lcode=120 (біт). LZSS: 0‘A’ 1<11,1> 0‘B’ 0‘C’ 0‘D’ 1<7,2> 1<8,1> 1<11,1> 1<10,2> 1<5,1> 1<2,1> 1<11,1>; Lcode=92 (біт);
LZ77: <0,0,‘К’><0,0,‘И’><0,0,‘Б’><0,0,‘Е’><0,0,‘Р’> <0,0,‘Н’> <9,1,‘Т’> <5,1,‘К’> <0,0,‘И’>; Lcode=135 (біт). LZSS: 0‘К’ 0‘И’ 0‘Б’ 0‘Е’ 0‘Р’ 0‘Н’ 1<9,1> 0‘Т’ 1<5,1> 1<3,2>; Lcode=84 (біт);
LZ77: <0,0,‘С’> <0,0,‘Т’> <0,0,‘Р’> <0,0,‘А’> <0,0,‘Н’> <11,1,‘Ы’> <0,0,‘Й’> <0,0,‘ ’> <3,4,‘Н’> <11,1,‘И’> <0,0,‘К’>; Lcode=165 (біт). LZSS: 0‘С’ 0‘Т’ 0‘Р’ 0‘А’ 0‘Н’ 1<11,1> 0‘Ы’ 0‘Й’ 0‘ ’ 1<3,4> 1<3,2> 0‘И’ 0‘К’; Lcode=111 (біт);
LZ77: <0,0,‘B’> <0,0,‘D’> <0,0,‘C’> <9,2,‘D’> <8,1,‘D’> <6,2,‘C’> <4,3,‘B’> <10,2,‘D’><3,1,‘C’>; Lcode=135 (біт). LZSS: 0‘B’ 0‘D’ 0‘C’ 1<9,2> 1<8,2> 1<6,3> 1<4,4> 1<9,2> 1<10,2> 1<3,2>; Lcode=76 (біт).
AABCDAACCCCDBB;
 =120 (біт);
=120 (біт);
 =92
(біт);
=92
(біт);/WED/WE/WED/WEB/WEE/WEB/WEE/E;
 =150(біт);
=101(біт);
=150(біт);
=101(біт);ВО ДВОРЕ ТРАВА НА ТРАВЕ ДРОВА; =225 (біт); =192 (біт);
LZ78: <0,‘A’> <1,‘B’> <0,‘C’> <0,‘D’> <1,‘A’> <3,‘C’> <6,‘D’> <0,‘B’> <0,‘B’>; Lcode=108 (біт). LZW: 0‘A’ 0‘A’ 0‘B’ 0‘C’ 0‘D’ <256> 0‘C’ <262> <259> 0‘B’ 0‘B’; Lcode=99 (біт);
LZ78: <0,‘К’> <0,‘И’> <0,‘Б’> <0,‘Е’> <0,‘Р’> <0,‘Н’> <4,‘Т’> <2,‘К’> <0,‘И’>; Lcode=108 (біт). LZW: 0‘К’ 0‘И’ 0‘Б’ 0‘Е’ 0‘Р’ 0‘Н’ 0‘Е’ 0‘Т’ 0‘И’ <256>; Lcode=90 (біт);
LZ78: <0,‘C’> <0,‘Т’> <0,‘Р’> <0,‘А’> <0,‘Н’> <5,‘Ы’> <0,‘Й’> <0,‘ ’> <1,‘Т’> <3,‘А’> <5,‘Н’> <0,‘И’> <0,‘К’>; Lcode=156 (біт). LZW: 0‘С’ 0‘Т’ 0‘Р’ 0‘А’ 0‘Н’ 0‘Н’ 0‘Ы’ 0‘Й’ 0‘ ’ <256> <258> <260> 0‘И’ 0‘К’; Lcode=126 (біт);
LZ78: <0,‘B’> <0,‘D’> <0,‘C’> <1,‘D’> <2,‘C’> <5,‘B’> <3,‘B’> <2,‘D’> <4,‘B’> <2,‘B’> <0,‘C’>; Lcode=132 (біт). LZW: 0‘B’0‘D’0‘C’ <256> <257> <257> 0‘B’ <258> 0‘D’ 0‘D’ <256> <266> 0‘C’; Lcode=117 (біт);
AABCDAACCCCDBB;
 =108 (біт);
=108 (біт);
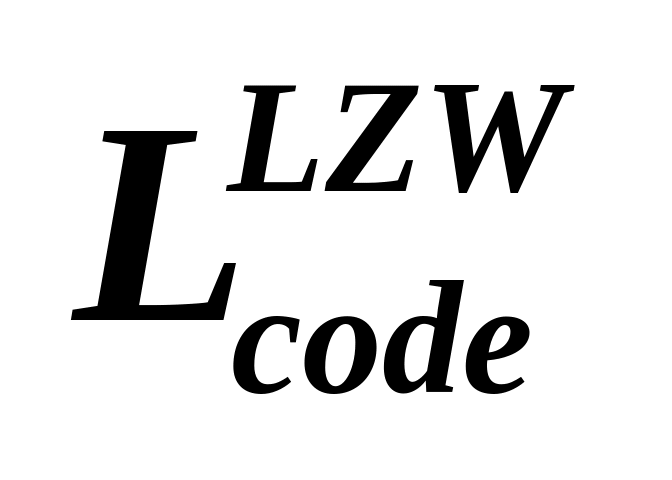 =99 (біт);
=99 (біт);/WED/WE/WED/WEB/WEE/WEB/WEE/E; =168(біт); =144 (біт);
ВО ДВОРЕ ТРАВА НА ТРАВЕ ДРОВА; =234 (біт);
 =207 (біт).
=207 (біт).
Частина III Розділ 9
P(Y=00/X=00)=pp, P(Y=00/X=01)=pq, , P(Y=00/X=11)=qq, ;
0,3%; 7,7 %;
Даний код є лінійним систематичним блоковим;
 ;
;
 ;
код здатний
виявляти 2 і виправляти 1 помилку;
;
код здатний
виявляти 2 і виправляти 1 помилку;000 0000000, 001 0011001, 010 0101010, , 111 1111111; код виявляє помилки кратності 2 і виправляє помилки кратності 1; Pпом=3p4q3+3p3q4+q73p4q3+3p3q4; 1001100100, 01010110101010 010, 00111010011001 001;
0000000, 0010010, 0100101, 0110111, 100 1001, 1011011, 1101100, 1111110; dmin=1; Pпом=p3q+3p2q2+3pq3; код виявляє тільки три ситуації наявності однієї помилки в коді з чотирьох можливих ;
dmin=3, код виявляє 2 і виправляє 1 помилку; Pпом=2p3q3+q62p3q3; 101110101010;010100010101;101111111111;
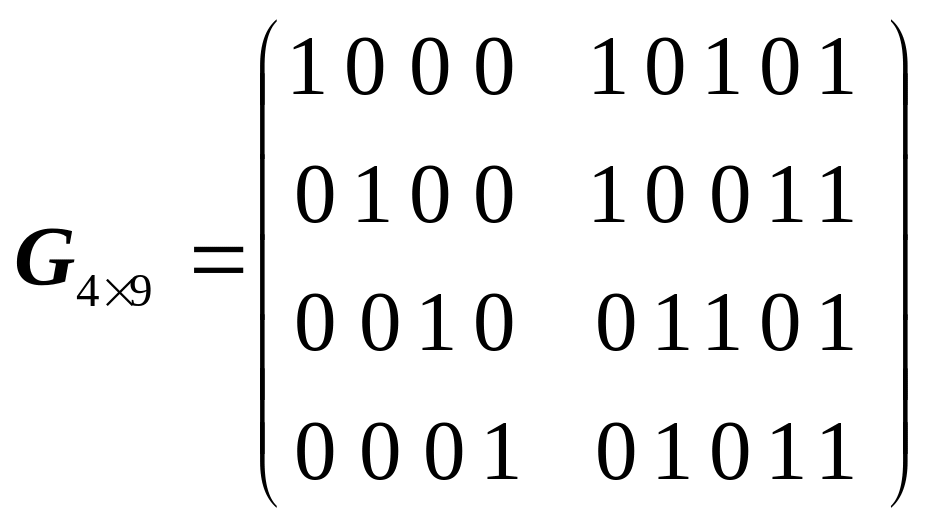 ;
Pпом=9p5q4+6p3q69p5q40,899610-15;
;
Pпом=9p5q4+6p3q69p5q40,899610-15;1101110011100111100110000;
![]() ;
;
00110000000001110011000000000011001000000;
00000011111011110000001111001111000001110;
01010000000001110100000000000101010000000; надлишковість коду до0,44.
Частина III Розділ 10
 ;
S=(y2+y3+y4,
y1+y2+y5,
y1+y2+y3+y6);
;
S=(y2+y3+y4,
y1+y2+y5,
y1+y2+y3+y6);101101011, 001001110; 011001011101011, 110100110110110, 001111 001110001;
S=(y1+y4+y5, y2+y5+y6, y3+y4+y6); 000000000, 001001101, 010010011, 011 011110, , 111111000;
S=(y1+y2+y3+y4+y5, y1+y3+y4+y6, y1+y2+y4+y7, y1+y2+y3+y8);
S=(y1+y2+y5, y3+y4+y6, y1+y3+y7, y2+y4+y8, y1+y2+y3+y4+y9); код виявляє помилки кратності 3 і виправляє помилки кратності 1;
00100010011, 10101010101, 11101110010; S=(y1+y2+y4+y5, y1+y2+y3+y6, y2+y3+y4+y7); код виявляє помилки кратності 2 і виправляє помилки кратності 1;
00100010111, 10101010001, 11101110010; 101010110100011010, 00101010010111 0010; S=(y1+y3+y4+y5, y1+y2+y3+y6, y2+y3+y4+y7); код здатний виявляти 2 і виправляти 1 помилку;
0110010 0110011 0110, 1101001 1101, 0111100 0111, 0011110 0010110 0010;
1101001 1100; 0110011 0010; 0111100 0110; 0011110 0011;
 ;
n=7,
k=4;
dmin=3;
;
n=7,
k=4;
dmin=3;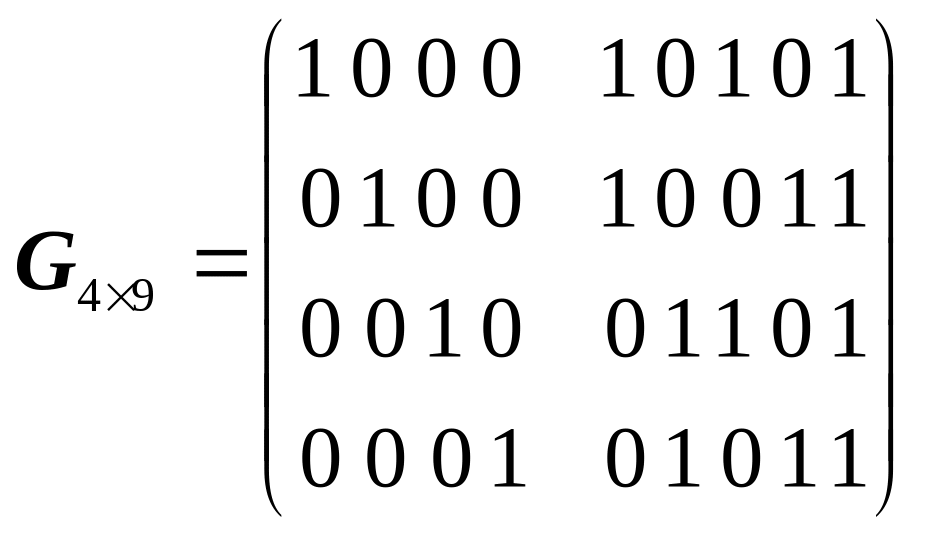 .
.
Частина III Розділ 11
1100110 10111000110, 1010111 10110101111;
![]() ;
надлишковість
коду к0,364;
;
надлишковість
коду к0,364;
1010 1011010, 1100 0111100; 1011 0110011;
 ;
к0,429;
;
к0,429;11001
111110011, 10100101101000, 10110 011001100;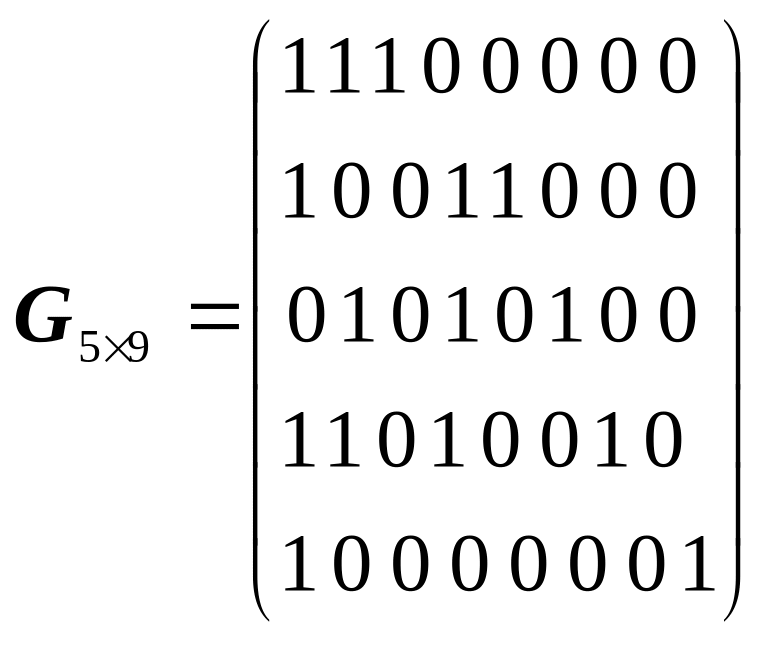 ;
надлишковість
к0,444;
;
надлишковість
к0,444;110
011110, 101101101, 011110011, 111001011; ;
надлишковість
к=0,5;
;
надлишковість
к=0,5;11111010110 011111101010110;
011001
1000110101; 1000110010000011; к=0,4;0110010
10001101010; 100011111100001111; к0,364;01100100
100011010100, 10001101001100011101;110110001010110 11001010110;11011001001100 0100;10111011010101 1101;1010101 1101.
Частина III Розділ 12
0100
01100010100, 10001101110011101111001, 11110100011100110;
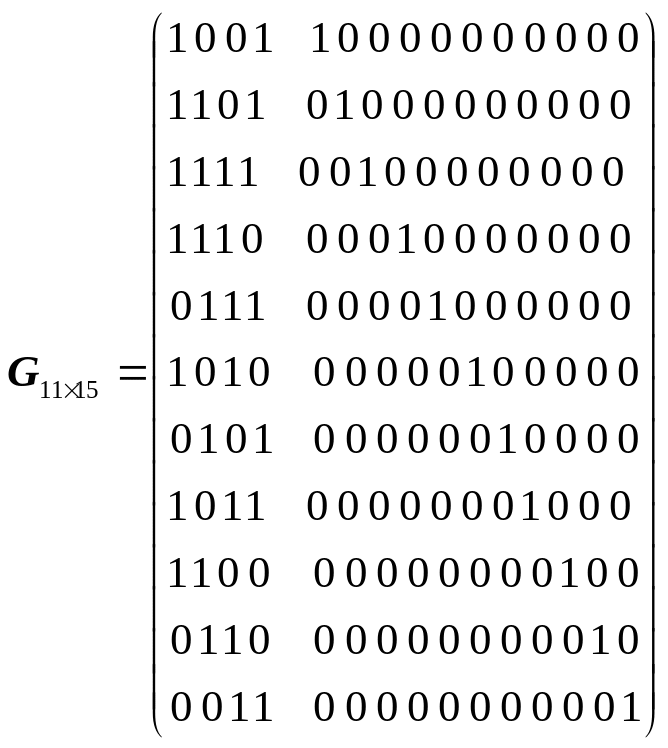 ;
;010111101011111
011111101011111;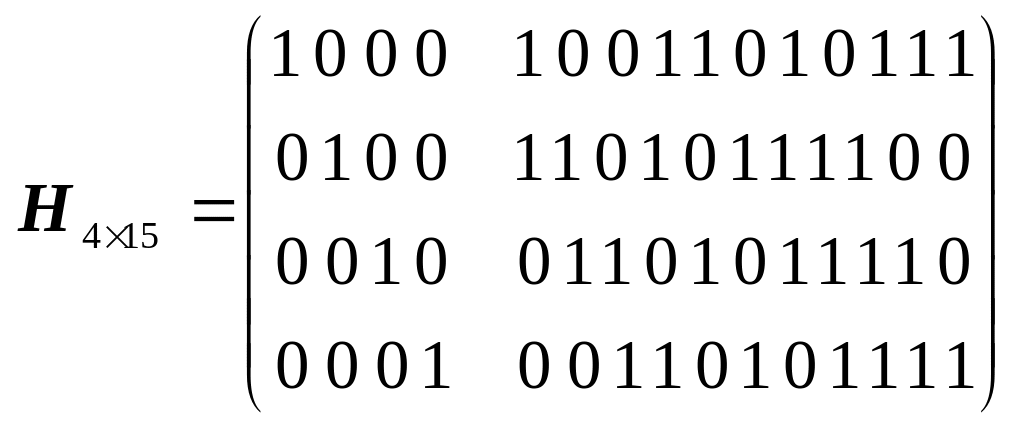 ,
10010111011
,
10010111011
111110010111011,
код виявляє
2 і виправляє 1 помилку;
dmin=4; код виявляє 3 і виправляє 1 помилку; Pпом=7p3q46,99810-16;
1100
100011110101100, 0011110101100100011; dmin=6; код здатний виявляти помилки кратності 5 і виправляти помилки кратності 2, ймовірність невиявлення помилки Pпом=p9q6+7p8q7+3p7q8+p5q10;01110110111010,10110101011000;01110110111001,10111011011100; ;
;11010111001011 011,11100111110010 010;
011
1010011, 1101001110, 1010011101.
Список використаної та рекомендованої літератури
Блейхер Р. Теория и практика кодов, контролирующих ошибки. – М.: Мир, 1986.
Жураковський Ю.П., Полторак В.П. Теорія інформації та кодування: Підручник. – К.: Вища школа, 2001. – 255 с.
Кузьмин И. В. Основы теории информации и кодирования. – Минск: Вышэйшая школа,1986.
Лидовский В.В. Теория информации: Уч. пособие. - М.: Компания Спутник+, 2004. - 111 с.
Питерсон Р., Уэлдон Э. Коды, исправляющие ошибки. – М.: Мир, 1976.
Стратонович Р.Л. Теория информации. – М: Изд-во “Сов. Радио”, 1975.
Хемминг Р.В. Теория информации и теория кодирования. – М. Радио и связь, 1983.
Цымбал В.П. Теория информации и кодирование. – К. Вища школа, 1992. – 263 с.
Чисар И., Кернер Я. Теория информации. – М.: Мир, 1985.
Шеннон К.-Э. Работы по теории информации и кибернетике. – М.: Изд-во иностр. Лит., 1963. 830 с.
Шульгин В. И. Основы теории передачи информации: Учебное пособие. Ч. I. Экономное кодирование. – Харьков: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2002. - 100 с.
Шульгин В. И. Основы теории передачи информации: Учебное пособие. Ч. II. Помехоустойчивое кодирование. – Харьков: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2002. – 90 с.
Предметний покажчик
A
ASCII
таблиця кодування 7
L
LZ-методи 109
LZ77 109, 110
LZ78 110, 114
LZSS 109, 113
LZW 110, 117
а
адаптивний (динамічний) алгоритм Хаффмена 93
аналогова
інформація 7
аналогово-цифровим перетворювачем 8
ансамблем повідомлень 10
арифметичного кодування 80
архівації
системи стиснення 129
б
байт 13
без втрат інформації
системи стиснення 130
безнадмірні 10
безумовною
ентропія 28
біт 13
блоковим кодом 134
блоковим кодом k-го порядку 72
блокових кодів 134
блокові коди 72
бодах (baud) 8
в
вагою Хеммінга 153
вектор помилок 150
вектором Крафта, 60
величиною спотворень 131
верхньою границею Варшамова-Гильберта 155
взаємна інформація 16
взаємна кількість інформації I(X, Y) 38
виправлення кодом помилок 154
високоефективні
системи стиснення 129
виявлення кодом помилок 154
відстанню Хеммінга 154
властивості
ентропії 15
кількості інформації і ентропії 17
циклічних кодів 175
В
Властивості 37
умовної ентропії 34
в
властивості завадостійких (коректувальних) кодів 134
вторинним алфавітом 10
г
границі стиснення інформації 71
д
двійковим полем GF(2) 136
двійкові (бінарні) коди 10
двійкового симетричного каналу 137
декодер 128
декодування циклічного коду
способ 183
дискретна
інформація 7
Д
Ділення поліномів 173
Добутком двох поліномів 172
д
додаванням
за модулем 2 136
достатні умови існування завадостійкого коду 155
е
економним кодуванням 55
ентропією джерела 14
Е
Ентропія об'єднання двох джерел 36
з
з контролем парності
код 136
З
Завадостійке кодування 134
Загальна умовна ентропія 33
з
зворотна теорема кодування джерела за наявності завад 44
згорткових кодів 135
і
із втратами
системи стиснення 130
інформаційні втрати 41
інформація 9
ітеративним
код 139
К
Канал зв'язку 10
к
каналом без шуму 39
каскадних
способи стиснення 129
квантователь 131
кількість інформації 12, 13
К
Кількість інформації 40
Кодер джерела 128
к
коди Хеммінга 164
кодів без пам'яті 61
кодів з пам'яттю 72
кодова комбінація 10
К
Кодовий синдром 151
к
кодовим синдромом 150
циклічного коду 179
кодовим словом 148
кодовими словами 134
кодового дерева 56
кодового поліному 176
кодом 10
К
Кодування 10
к
коефіцієнт стиснення 129
комбінованих
способи стиснення 129
компактним
код 60
контрольними
символи 134
л
ланцюгами Маркова 29
Л
Лінійний блоковий систематичний (k, n)- код 148
л
лінійним
код 135
лінійних
способи стиснення 129
м
матричних
способи стиснення 129
М
Метод блокування повідомлень 72
м
мінімальною кодовою відстанню 154
модель
системи передачі інформації 29
модеми 8
н
надлишковими
символи 134
наслідком теореми кодування джерела у відсутності шуму 64
Н
Наслідком теореми Шеннона 69
н
неабсолютного статистичного взаємозв'язку джерел 40
недвійкові (багатопозиційні, q-коди)
коди 10
некоректувальні 10
необхідні умови існування завадостійкого коду 155
неперервна
інформація 7
нерівність Крафта 60
нерівномірними
коди 10
неруйнуюче стиснення 130
нижньою границею Хеммінга 155
нижня границя Плоткина 155
низько-, середньо- і високошвидкісні
системи стиснення 129
низькоефективні
системи стиснення 129
о
оптимальні нерівномірні коди 35
п
первинним алфавітом 10
первинні
коди 10
перевірним поліномом 179
перевірними
символи 134
перевірною матрицею 148
передачі
системи стиснення 129
повний статистичний взаємозв'язок джерел 39
П
Полем 135
Поліном синдрому 179
Поліноміальним
код 173
п
префіксні коди 58
П
Префіксною множиною 60
п
примітивним рівномірним
код 57
продуктивність джерела 38
пропускною здатністю 41
канала 10
р
рівномірними
коди 10
руйнуюче стиснення 130
ряд Фур’є 8
с
семантичної інформації 14
семантичної надмірності 16
синдром 165
синдрому 153
система перевірних рівнянь 147
С
Систематичний
код 135
с
системах стиснення без втрат 130
системах стиснення із втратами 131
С
Словникові алгоритми 109
с
спектром функції 9
статистична надмірність 15
статистична незалежність джерел 39
статистичним
кодування 35, 60
статистичної надмірності 34
стисненням інформації 55
С
Сумою двох поліномів 172
т
таблиці кодування 7
Т
Твірна матриця циклічного коду 181
т
твірним многочленом 173
твірним поліномом 176
твірної матриці 147, 155
твірної матриці циклічного коду 181
теорема кодування
при наявності завад 43
Т
Теорема Шеннона про кодування дискретного джерела
при відсутності завад 43
т
теоремою дискретизації Шеннона-Котельнікова 8
Т
Теорія інформації 7
у
умовна ймовірність 28
умовною
ентропія 29
У
Упорядкованим деревом Хаффмена 93
ф
формулою Бернуллі 137
Х
Хартлі
формула 15
Хаффмана
алгоритм 62
Хаффмена
адаптивний (динамічний) алгоритм 93
упорядковане дерево 93
Хеммінга
вага 153
відстань 154
коди 164
Ц
Циклічним
код 179
ц
циклічні коди 175
циклічного
код 177
цифро-аналоговим перетворювачем 8
цифрова
інформація 7
Ч
Часткова умовна ентропія 33
ш
швидкість передачі інформації 39
швидкість стиснення 129
швидкістю стиснення 131
Ш
Шеннона-Фано
алгоритм 61
Шум 10
Зміст
С.
ПЕРЕДМОВА 6
Частина I Основи теорії інформації та кодування 7
Розділ 1 ОСНОВНІ ПОЛОЖЕННЯ ТЕОРІЇ ІНФОРМАЦІЇ 7
1.1 Предмет курсу. Види інформації. Теорема дискретизації 7
1.2 Базові поняття теорії інформації 9
1.3 Способи вимірювання інформації 11
1. 4 Ентропія джерела. Властивості кількості інформації та ентропії 14
Зразки розв'язування задач до розділу 1 17
Задачі до розділу 1 24
Розділ 2 ХАРАКТЕРИСТИКИ ДИСКРЕТНОГО КАНАЛУ ПЕРЕДАЧІ ІНФОРМАЦІЇ 28
2.1 Умовна ентропія 28
2.2 Модель системи передачі інформації 29
2.3 Види умовної ентропії 33
2.4 Ентропія об'єднання двох джерел інформації 36
2.5 Продуктивність дискретного джерела інформації. Швидкість передачі інформації 38
2.6 Інформаційні втрати при передачі інформації по дискретному каналу зв'язку 39
2.7 Пропускна здатність дискретного каналу. Основна теорема про кодування дискретного джерела 41
Зразки розв'язування задач до розділу 2 44
Задачі до розділу 2 50
Контрольні запитання до розділів 1-2 52
Частина II Економне кодування інформації. Статистичні та словникові методи стиснення даних 55
Розділ 3 ОПТИМАЛЬНІ СТАТИСТИЧНІ МЕТОДИ СТИСНЕННЯ ІНФОРМАЦІЇ 55
3.1 Способи задання кодів. Статистичне кодування 55
3.2 Елементи теорії префіксних множин 60
3.3 Оптимальні методи статистичного стиснення інформації Шеннона-Фано і Хаффмена 61
Зразки розв'язування задач до розділу 3 65
Задачі до розділу 3 68
Розділ 4 ЗАСТОСУВАННЯ СТАТИСТИЧНИХ АЛГОРИТМІВ СТИСНЕННЯ ДО БЛОКІВ ПОВІДОМЛЕННЯ 69
4.1 Теоретичні границі стиснення інформації 69
4.2 Метод блокування повідомлення 71
Зразки розв'язування задач до розділу 4 75
Задачі до розділу 4 78
Розділ 5 АРИФМЕТИЧНЕ КОДУВАННЯ 80
Зразки розв'язування задач до розділу 5 86
Задачі до розділу 5 91
Розділ 6 АДАПТИВНИЙ АЛГОРИТМ ХАФФМЕНА З УПОРЯДКОВАНИМ ДЕРЕВОМ 93
Зразки розв'язування задач до розділу 6 99
Задачі до розділу 6 107
Розділ 7 СЛОВНИКОВІ МЕТОДИ СТИСНЕННЯ ЗІВА-ЛЕМПЕЛА 109
7.1 Алгоритм LZ77 110
7.2 Алгоритм LZSS 113
7.3 Алгоритм LZ78 114
7.4 Алгоритм LZW 117
Зразки розв'язування задач до розділу 7 119
Задачі до розділу 7 125
Розділ 8 СИСТЕМИ СТИСНЕННЯ ІНФОРМАЦІЇ 128
8.1 Огляд типів систем стиснення інформації 128
8.2 Стиснення без втрат інформації 130
8.3 Стиснення із втратами інформації 131
Контрольні запитання до розділів 3-8 132
Частина III Завадостійке кодування інформації 134
Розділ 9 ОСНОВНІ ПРИНЦИПИ ЗАВАДОСТІЙКОГО КОДУВАННЯ. 134
ЛІНІЙНІ БЛОКОВІ КОДИ 134
9.1 Основні принципи 134
9.2 Елементи двійкової арифметики 135
9.3 Код з перевіркою на парність 136
9.4 Ітеративний код 138
Зразки розв'язування задач до розділу 9 139
Задачі до розділу 9 144
Розділ 10 СПОСОБИ ЗАДАННЯ ЛІНІЙНИХ БЛОКОВИХ КОДІВ. СИНДРОМНЕ ДЕКОДУВАННЯ ЛІНІЙНИХ БЛОКОВИХ КОДІВ 147
10.1 Способи задання лінійних кодів. Твірна матриця лінійного блокового коду 147
10.2 Перевірна матриця лінійного блокового коду 148
10.3 Кодовий синдром і виявлення помилок лінійним блоковим кодом 150
10.4 Синдромне декодування лінійних блокових кодів 151
10.5 Вага і відстань Хеммінга. Можливості лінійних кодів виявляти і виправляти помилки 153
Зразки розв'язування задач до розділу 10 156
Задачі до розділу 10 161
Розділ 11 КОД ХЕММІНГА 164
Зразки розв'язування задач до розділу 11 167
Задачі до розділу 11 170
Розділ 12 ПОЛІНОМІАЛЬНЕ КОДУВАННЯ ІНФОРМАЦІЇ. ЦИКЛІЧНІ КОДИ 172
12.1 Операції над поліномами в полі двійкових символів GF(2) 172
12.2 Поліноміальні коди 173
12.3 Циклічні коди 175
12.4 Синдром і виправлення помилок у циклічних кодах 179
12.5 Твірна і перевірна матриці циклічного коду 180
12.6 Способи декодування циклічного коду 183
Зразки розв'язування задач до розділу 12 184
Задачі до розділу 12 194
Контрольні запитання до розділів 9-12 195
Відповіді до задач 198
Список використаної та рекомендованої літератури 208
Предметний покажчик 209
Зміст 212
1 Шеннон К. Работы по теории информации и кибернетике. - М., Изд-во иностранной литературы, 1963.
2 Фано Р. Передача інформації. Статистична теорія зв'язку. –М.:
Мир, 1965.
