12.3 Циклічні коди
Серед поліноміальних кодів найпоширеніші циклічні коди.
Визначення. Лінійний блоковий (k, n) - код називається циклічним, якщо в результаті циклічного зсуву кодового слова виходить інше кодове слово даного коду. Іншими словами, якщо u=(u0, u1, …, un-1) – кодове слово, то і v=(un-1, u0, u1, …, un-2), отримане циклічним зсувом елементів ui, - кодове слово.
Наведемо властивості циклічних кодів.
Для циклічного (k, n)- коду кожний ненульовий поліном повинен мати степінь принаймні (n-k), але не більше n-1;
Існує тільки один кодовий поліном g(x)=1 + g1x +g2x2 + … + +gn-k-1xn-k- + xn-k степеня (n-k), що є дільником кожного кодового полінома u(x)=m(x)g(x), цей поліном називається твірним поліномом коду.
Припустимо, треба закодувати деяку послідовність m=(m0, m1, m2, …, mk-1). Відповідний їй поліном матиме вигляд
m(x)=m0+m1x+m2x2+ … +mk-1xk-1. (3.17)
Помножимо m(x) на xn-k, що рівнозначно зсуву двійкової послідовності m=(m0, m1, m2, …, mk-1) на n-k розрядів праворуч. У результаті отримаємо поліном степеня n-1 або меншого
xn-km(x)=m0xn-k+m1xn-k+1+ … +mk-1xn-1. (3.18)
Скориставшись теоремою ділення поліномів (3.14), можна записати
xn-km(x)=q(x)g(x) + ρ(x), (3.19)
де q(x) і ρ(x) - частка і остача від ділення полінома xn-km(x) на твірний поліном g(x).
Оскільки степінь твірного полінома g(x) r=(n-k), то степінь остачі ρ(x) не більше (n-k-1), тобто
ρ(x)=ρ0+ ρ1x+ ρ2x2+…+ ρn-k-1xn-k-1. (3.20)
Використовуючи правила арифметики з GF(2), вираз (3.19) можна записати так:
ρ(x) + xn-km(x) = q(x)g(x). (3.21)
Звідси випливає, що поліном ρ(x)+xn-km(x) кратний g(x) і має степінь не більше n-1.
Отже, поліном ρ(x)+xn-km(x) є кодовим поліномом, що відповідає многочлену інформаційної послідовності m(x).
Розкривши вираз (3.21), отримуємо
ρ(x)+m(x)xn-k=ρ0+ρ1x+ρ2x2+…+ρn-k-1xn-k-1+m0xn-k+m1xn-k+1 +…+
+ mk-1xn-1, (3.22)
що відповідатимемо кодовому слову
u=(0, 1, …, n-k-1, m0, m1, m2, …, mk-1),
де 0, 1, …, n-k-1 – перевірні символи; m0, m1, m2, …, mk-1 - інформаційні символи.
Відтак, кодове слово циклічного коду складається з перевірної частини з (n-k) перевірних символів і інформаційної частини m завдовжки k символів. Перевірні символи є коефіцієнтами полінома ρ(x) – остачі від ділення кодового слова u(x)=m(x)xn-k на твірний поліном g(x).
Приклад 2 Закодуємо послідовність m=(0111) циклічним кодом, заданим твірним поліномом g(x)=1+x+x3.
Вектору m=(0111) відповідає поліном m(x)=x+x2+x3.
Помножимо m(x) на xn-k=x3, де n-k – кількість перевірочних символів: m(x) xn-k=m(x)x3=(x+x2+x3) x3=x4+x5+x6, або виконаємо зсув елементів інформаційної послідовності m(x) на r=3 розряди праворуч: (0111) (0000111).
Розділимо добуток m(x)xn-k на твірний поліном коду g(x):
x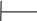
6
+ x5
+ x4
x3+x+1
+ x6 + x4 + x3 x3+x2
x5 + x3
+ x5 + x3 + x2
x2= ρ(x).
Многочлен остачі від ділення має степінь n-k-1 і такий вигляд:
ρ(x)= 0∙x0 + 0∙x1 + 1x2.
Отже, кодовий поліном заданої інформаційної послідовності:
u(x)=ρ(x) + xn-km(x)=x2 + x4 + x5 + x6=0∙x0 + 0∙x1 + 1x2 + 0∙x3 + +1x4 + 1x5 +1x6,
що відповідає кодовому слову u=(0010111), де перші три символи перевірні.
Таким чином, алгоритм побудови циклічного (k, n)- коду для послідовності m=(m0, m1, m2, … , mk-1) такий:
1) многочлен інформаційної послідовності m(x) множиться на xn-k, тобто зсувається праворуч на n-k розрядів;
2) отриманий у такий спосіб поліном ділиться на твірний поліном коду g(x);
3) остача від ділення xn-km(x) на g(x) додається до xn-km(x), тобто записується в молодших n-k розрядах.
Ще однією важливою властивістю циклічного (k, n)- коду є те, що твірний поліном g(x) ділить без остачі двочлен xn+1, тобто комбінації лінійного коду мають властивість циклічності при виконанні умови
xn+1=g(x)h(x). (3.23)
Кожний такий двочлен xn+1 може бути розкладений на декілька незвідних поліномів – таких поліномів, які не можуть бути подані як добуток многочленів меншого степеня, тобто вони діляться або самі на себе, або на 1.
Як твірні поліноми різних циклічних кодів використовуються незвідні поліноми і їх добутки, оскільки вони є дільниками двочлена xn+1. Деякі з твірних поліномів наведені у табл. 3.4.
Таблиця 3.4
Твірний поліном g(x) |
Двійковий запис полінома |
1+x |
11 |
1+x+x2 |
111 |
1+x+x3 |
1101 |
1+x2+x3 |
1011 |
1+x+x4 |
11001 |
1+x3+x4 |
10011 |
1+x+x2+x4 |
11101 |
1+x2+x3+x4 |
10111 |
1+x+x2+x3+x4 |
11111 |
Продовження табл.3.4
Твірний поліном g(x) |
Двійковий запис полінома |
1+x2+x5 |
101001 |
1+x3+x5 |
100101 |
1+x+x2+x3+x5 |
111101 |
1+x+x2+x4+x5 |
111011 |
1+x4+x5+x6 |
1000111 |
1+x+x2+x5+x6+x7+x8 |
111001111 |
1+x3+x5+x9 |
1001010001 |
1+x+x5+x6+x10+x11 |
110100100011 |
1+x+x2+x3+x5+x7+x8+x11 |
111101011001 |
1+x3+x4+x6+x8+x9+x10+x11 |
100110101111 |
1+x+x2+x3+x4+x12+x13+x14+x15 |
1111100000001111 |
1+x5+x12+x16 |
10000100000010001 |
Визначення. Поліном h(x) степеня k, що є часткою від ділення двочлена xn+1 на твірний поліном коду g(x), називається перевірним поліномом. Оскільки h(x) однозначно зв'язаний з g(x), то він також визначає код.
Спираючись на вищевикладене, можна дати інше визначення двійкового циклічного коду.
Визначення. Циклічним називається лінійний (k, n)- код, усі 2k кодові комбінації якого подані поліномами степеня n-1 і менше, які діляться без остачі на деякий поліном g(x) степеня r=n-k, що є дільником двочлена xn+1.