Розв'язання

Перевірна матриця заданого коду має розмірність (n-k, n) і таку структуру:

,

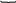де - транспонована перевірна (права) частина твірної матриці G; - одинична підматриця.

Кількість інформаційних елементів коду k=4, перевірних r=3, довжина кодових слів n= k+r=7.

Кодові слова даного лінійного блокового коду будуються так:

u=(u₁, u₂, , u_n) = (m₁, m₂, m₃, m₄, r₁, r₂, r₃),

де m₁, m₂, m₃, m₄ - інформаційні символи; r₁, r₂, r₃ – перевірні символи, що додають кодером до блоку повідомлення m=(m₁, m₂, m₃, m₄).

Знайдемо систему перевірних рівнянь, що визначають правила знаходження перевірних символів (контрольних сум) коду.

1-й спосіб.

З рівняння кодового синдрому

визначаємо правила знаходження перевірних символів коду:

()

2-й спосіб.

Кодове слово лінійного блокового коду утворюється множенням інформаційного повідомлення на твірну матрицю:

Звідси випливає система перевірних рівнянь коду ().

Закодуємо задані інформаційні послідовності, помноживши їх на твірну матрицю коду G або обчисливши контрольні суми з () і дописавши їх у правій частині кодового слова:

1. (1010) =(1010011); (1010)(1010011).

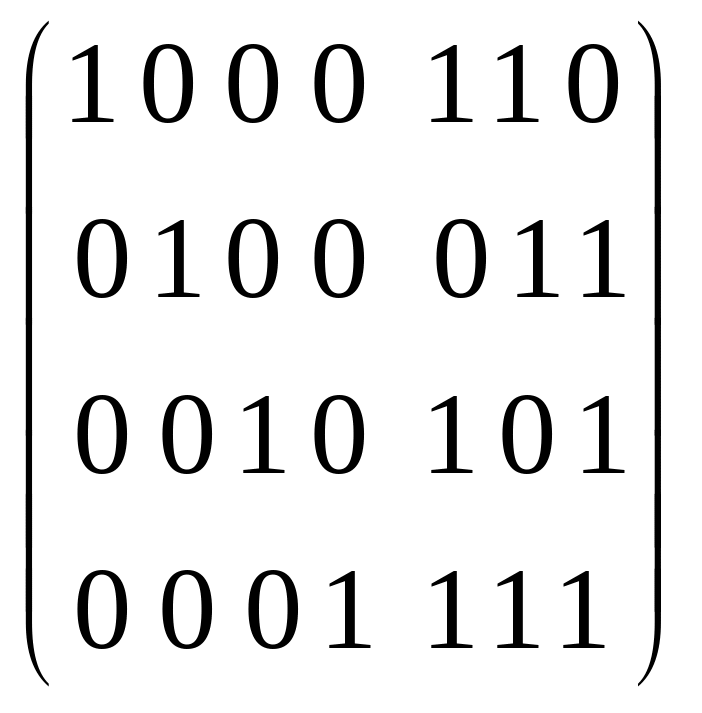2. (1110) =(1110000); (1110)(1110000).

На приймальному боці обчислюється вектор синдрому

де y – прийнята кодована послідовність; H^ – перевірна матриця.

Кодовий синдром служить ознакою наявності помилок у прийнятій послідовності: якщо вектор синдрому дорівнює нулю, то прийнята послідовність є кодовим словом даного коду, інакше в ній є помилки.

Використання синдрому дозволяє не тільки виявляти, але й виправляти однократні помилки в коді: у випадку наявності в прийнятій послідовності однієї помилки вектор синдрому збігається з тим із стовпців перевірної матриці, номер якого відповідає номеру помилкового біта.

Перевіримо на наявність помилок комбінації 1010101, 1000100, і у випадку виявлення помилки виправимо її.

Для цього обчислюємо синдром прийнятого вектора:

1. (1010101)H^=(1010101)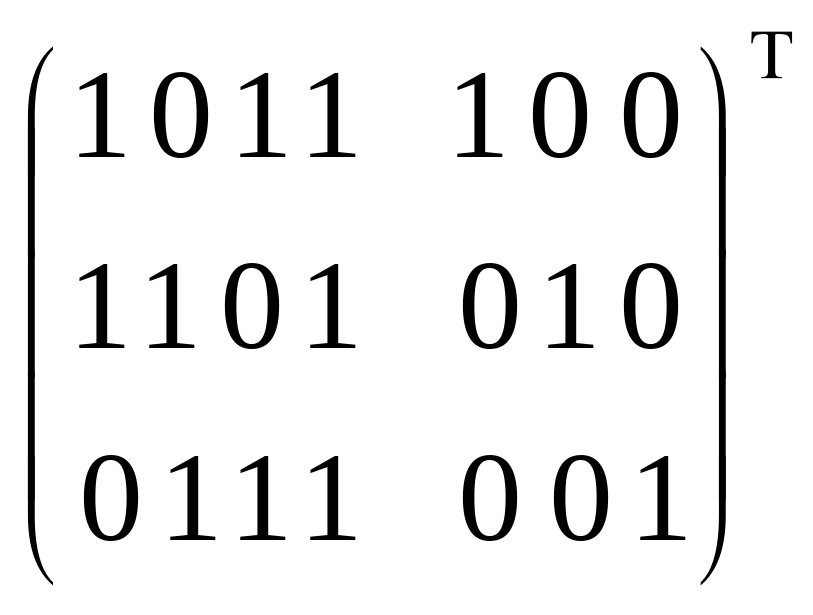 =(110)0, отже, у даній послідовності є помилка. Кодовий синдром S=(110) збігається із 1-м стовпцем перевірної матриці, що свідчить про наявність помилки у 1-му біті.

Виправляємо помилку: (1010101) (0010101).

Декодуємо послідовність, вилучивши контрольні суми:

(0010101) (0010).

2. (1000100)H^=(1000100)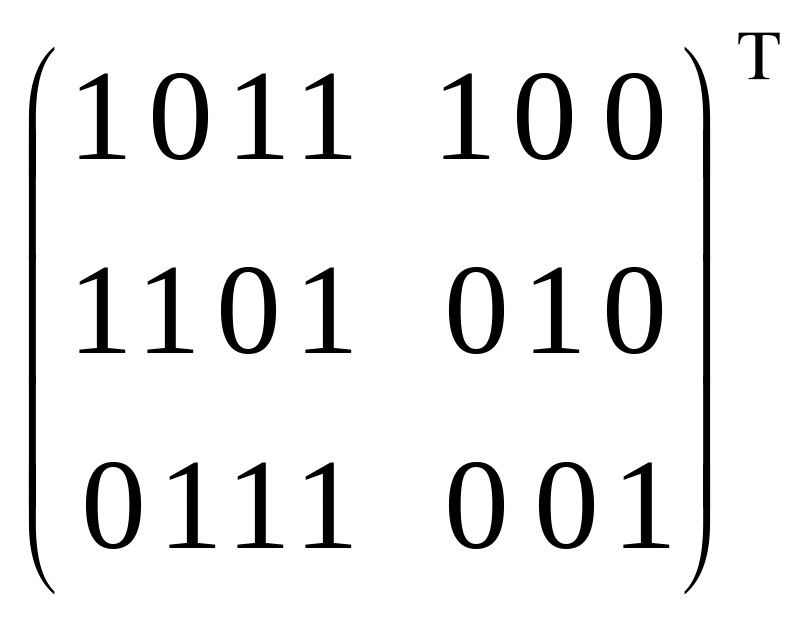 =(010)0 – кодовий синдром S=(010) збігається з 6-м стовпцем перевірної матриці, що свідчить про помилку у 6-му біті.

Виправляємо помилку: (1000100)(1000110).

Декодуємо послідовність, прибравши контрольні суми: (1000110) (1000).

Приклад 2 Побудувати твірну матрицю лінійного блокового коду, здатного виправляти поодинокі помилки при передачі 8 повідомлень. Побудувати перевірну матрицю коду. Навести приклад кодування і декодування повідомлень із виявленням і виправленням помилки.

Розв'язання

Кількість бітів, необхідна для кодування 8 повідомлень різними комбінаціями двійкового коду, визначається з нерівності

N  2^k,

де N – об'єм алфавіту джерела повідомлень; k – довжина кодової комбінації у бітах.

Звідки випливає, що k  log₂ N.

У даному випадку для кодування N=8 повідомлень необхідна кількість бітів k  3.

Довжина кодових слів при кодуванні лінійним блоковим кодом інформаційних повідомлень довжиною k символів n= k+r, де r – кількість перевірних символів, що додаються до інформаційного повідомлення для забезпечення можливості виявлення і/або виправлення помилок, що виникають при передачі по каналу зв'язку із завадами.

Знайдемо кількість перевірних розрядів r, необхідну для виправлення помилок кратності l=1.

Для того щоб лінійний блоковий код міг виправляти помилки кратності не більшої l, необхідно і достатньо, щоб найменша кодова відстань між його словами d_min відповідала нерівності

d_min ≥ 2l+1.

У даному випадку для виправлення помилок ваги l=1 мінімальна кодова відстань d_min  3.

Мінімальну кількість перевірних розрядів r визначаємо, скориставшись формулою нижньої границі Плоткина:

r   2d_min - 2 – log₂ d_min.

У даному випадку необхідна кількість перевірних елементів r =  23 – 2 – log₂ 3    4 – 1,585 =3.

Тоді довжина кодового слова n= k+r = 3+3=6.

Твірна матриця лінійного блокового коду складається із двох частин: інформаційної I_k×k (одиничної підматриці) і перевірної Р_kr. Перевірна підматриця P_k(n-k) будується підбором r-розрядних комбінацій з кількістю одиниць у рядку ≥ d_min-1 і кодовою відстанню між рядками ≥d_min-2. При цьомусі рядки твірної матриці лінійно незалежні, вага кожного кодового слова, що входить у твірну матрицю, і кодова відстань між ними ≥d_min.

Наведемо можливий варіант твірної матриці лінійного блокового (3,6)-коду:

.

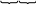I_k×k P_k(n-k)

Перевірна матриця заданого коду складається із транспонованої перевірної частини твірної матриці P_(n-k)×k і одиничної підматриці I_(n-k)×(n-k):

.

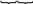P^_(n-k)-k I^_k×k

Виходячи з твірної матриці, будуємо таблицю всіх можливих кодових слів заданого коду:

(m₁, m₂, m₃) (u₁, u₂, u₃, u₄, u₅, u₆)= =(m₁, m₂, m₃, r₁, r₂, r₃),

де кодове слово u= mG_{(k, n)}.

1) (000)(000000); 2) (001)(001110);

3) (010)(010011); 4) (011)(011101);

5) (100)(100101); 6) (101)(101011);

7) (110)(110000); 8) (111)(111001).

Неважко переконатися, що мінімальна кодова відстань отриманого коду d_min=3.

Іншим способом таблицю кодів можна побудувати, розглянувши всі можливі лінійні комбінації (порозрядні суми за модулем 2) кодових слів, що входять у твірну матрицю коду.

Припустимо передається повідомлення m=(101).

Кодовим словом на виході кодера буде послідовність

u= mG = (101) = (101011). Нехай при передачі цього кодового слова по каналу зв'язку із завадами в ньому виникла помилка. Наприклад, прийнята послідовність y=(101111).

Для декодування прийнятої послідовності на прийомній стороні обчислюється кодовий синдром

S= yH^,

де y – прийнята кодована послідовність; H^ - транспонована перевірна матриця.

Обчислимо синдром прийнятого вектора y:

S= (101111) = (100)  0 - значення синдрому збігається із 4-м стовпцем перевірної матриці H, отже, помилка виникла в 4-му розряді.

Виправляємо помилку і декодуємо кодове слово так:

(101111)(101011)(101).

Задачі до розділу 10

1. Перевірна матриця лінійного блокового (3, 6)- коду має вигляд

.

Побудувати твірну матрицю і систему перевірних рівнянь коду. Визначити синдром виправлення однократних помилок в комбінаціях коду. Навести приклад виявлення і виправлення помилки кодом.

2. Перевірна матриця лінійного блокового (3, 6)- коду має вигляд

.

Побудувати твірну матрицю коду. Закодувати повідомлення 101, 001. Використовуючи синдром, визначити помилку (якщо вона є) і декодувати послідовності 011001; 110100; 001111.

3. Лінійний блоковий код заданий твірною матрицею вигляду

.

Побудувати перевірну матрицю коду. Визначити синдром виправлення поодиноких помилок цим кодом. Побудувати таблицю кодів. Навести приклад виявлення і виправлення помилки кодом.

4. Перевірна матриця коду має вигляд

.

Побудувати твірну матрицю коду. Визначити мінімальну кодову відстань Хеммінга і можливості коду виявляти і виправляти помилки. Визначити синдром виправлення поодиноких помилок кодом. Навести приклад виявлення і виправлення помилки.

5. Твірна матриця лінійного блокового коду має вигляд

.

Побудувати перевірну матрицю коду. Визначити синдром виправлення поодиноких помилок кодом і його можливості виявляти і виправляти помилки. Навести приклад виправлення помилки.

6. Твірна матриця лінійного блокового (4, 7)- коду має вигляд

.

Побудувати перевірну матрицю коду й закодувати комбінації 0010, 1010, 1110. Визначити синдром виправлення поодиноких помилок в комбінаціях заданого коду. Навести приклад виправлення помилки. Скільки помилок можна виявити/ виправити цим кодом?

7. Перевірна матриця лінійного блокового (4, 7)- коду має вигляд

.

Побудувати твірну матрицю коду. Закодувати комбінації 0010, 1010, 1110. Визначити синдром виправлення поодиноких помилок в комбінаціях заданого коду. Виправити помилку і декодувати послідовності 1010101, 0010101. Визначити можливості коду виявляти і виправляти помилки.

8. Перевірна матриця лінійного блокового (4, 7)- коду має вигляд

.

Використовуючи синдром, визначити помилку і декодувати прийняті комбінації 0110010, 1101001, 0111100, 0011110.

9. Твірна матриця лінійного блокового коду має вигляд

.

Визначити, які з комбінацій 1101001, 0110011, 0111100, 0011110 містять помилку, виправити їх і декодувати.

10. Розглянути лінійний блоковий (k, n)-код, кодове слово якого утворюється за правилом u=(x₁, x₂, x₃, x₄, x₁+x₃+x₄, x₁+x₂+x₄, x₂+x₃+x₄). Визначити перевірну матрицю коду і параметри n, k. Чому дорівнює мінімальна кодова відстань отриманого коду?

11. Розглянути лінійний блоковий (k, n)-код, кодове слово якого утворюється за правилом u=(x₁, x₂, x₃, x₄, x₁+x₂, x₃+x₄, x₁+x₃, x₂+x₄, x₁+x₂+x₃+x₄). Побудувати твірну матрицю коду.

12. Побудувати твірну матрицю лінійного блокового коду, здатного виправляти поодинокі помилки при передачі 16 повідомлень. Визначити синдром виправлення поодиноких помилок кодом. Навести приклад виявлення і виправлення помилки.

Розділ 11 КОД ХЕММІНГА

Найпоширенішими систематичними лінійними блоковими кодами є коди Хеммінга, до яких належать коди з мінімальною кодовою відстанню d_min=3, здатні виправляти поодинокі помилки.

При передачі кодового слова по каналу зв'язку можливе виникнення однократної помилки у будь-якому з його елементів. Кількість таких ситуацій дорівнює n. Отже, для того щоб визначити місце виникнення помилки, кількість різних комбінацій перевірних елементів повинна перевищувати кількість можливих помилкових ситуацій в коді плюс ситуація, коли помилки немає, тобто повинна виконуватися нерівність

. (3.9)

З цієї нерівності випливає мінімальне співвідношення перевірних і інформаційних розрядів, необхідне для виправлення кодом поодиноких помилок

. (3.10)

Для розрахунку основних параметрів коду Хеммінга можна задатися кількістю перевірних елементів r, тоді довжина кодових слів , а кількість інформаційних елементів k=n-r. Співвідношення між r, n і k зручно подати у вигляді такої таблиці (табл. 3.3).

Таблиця 3.3

k	1	1	2	3	4	4	5	6	7	8	9	10	11	11	12
r	2	3	3	3	3	4	4	4	4	4	4	4	4	5	5
n	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17

Характерною властивістю перевірної матриці лінійного блокового коду з d_min=3 є те, що її стовпці являють собою різні ненульові комбінації завдовжки r.

Хеммінгом запропоновано розміщувати стовпці перевірної матриці так, щоб i-й стовпець матриці, що відповідає номеру i помилкового розряду кодової комбінації, був двійковим поданням цього номера. Тоді синдром виправлення однократних помилок кодом Хеммінга є двійковим поданням номера розряду, в якому виникла помилка. Для цього перевірні розряди, що відповідають стовпцям одиничної підматриці перевірної матриці коду, повинні знаходитися не в правій частині кодового слова, а у позиціях з номерами степеня двійки, тобто 2⁰, 2¹, 2²,…, .

Наприклад, для r=3 перевірна матриця Хеммінга має вигляд

.

Для даного лінійного блокового (4, 7)- коду перший, другий, четвертий розряди (u₁, u₂, u₄) будуть перевірними, а третій, п'ятий, шостий і сьомий розряди (u₃, u₅, u₆, u₇) - символами інформаційного повідомлення у звичайному порядку, тобто (m₁, m₂ m₃, m₄) відповідно.

Отже, для (k, n)- коду Хеммінга в кожному кодовому слові u=(u₁, u₂, u₃, u₄, …, u₈, … u_n), r = n-k бітів з номерами степеня двійки є перевірними, а інші – бітами повідомлення, тобто кодування здійснюється так:

E(m₁, m₂, …, m_k) =(u₁, u₂, …, u_n) =(r₁, r₂, m₁, r₃, m₂, m₃, m₄, r₄,

m₅, m₆, …, m_k).

Перевірна матриця (k, n)- коду Хеммінга складається із r рядків і стовпців, що є двійковими комбінаціями числа i, де i - номер стовпця. Наприклад, для r = 2, 3, 4 перевірні матриці коду Хеммінга мають вигляд

; ;

.

Синдром, що визначає систему перевірних рівнянь коду, знаходиться із рівняння

u =0.

Наприклад, для r = 3 система перевірних рівнянь буде така:

Звідси визначають перевірні розряди (контрольні суми)

Щоб закодувати повідомлення m u, значеннями розрядів u_i, де i не дорівнює степеню двійки, будуть відповідні біти повідомлення у тому самому порядку, а перевірні розряди з індексами степеня двійки знаходяться з системи перевірних рівнянь. У кожне рівняння системи входить тільки одна контрольна сума.

Приклад 1 Закодуємо повідомлення m=(0111) (4, 7)-кодом Хеммінга.

Кодовим словом для заданого повідомлення m буде послідовність u=(u₁ u₂ 0 u₄ 1 1 1), де u₁, u₂, u₄ - контрольні суми r₁, r₂, r₃ відповідно.

Знаходимо контрольні суми з системи перевірних рівнянь:

r₁=u₁=u₃+u₅+u₇=m₁+m₂+m₄=0+1+1=0, r₂=u₂=u₃+u₆+u₇=m₁+m₃+m₄=0+1+1=0, r₃=u₄=u₅+u₆+u₇=m₂+m₃+m₄=1+1+1=1.

Отже, кодовим словом буде послідовність u=(0001111).

Декодування коду Хеммінга здійснюється у такий спосіб. Обчислюється синдром прийнятої послідовності y:

S=y ,

де - перевірна матриця коду. Якщо синдром нульовий вектор, то вважається, що слово передане без помилок, інакше значення синдрому відповідає двійковому поданню номера помилкового розряду. У цьому випадку потрібно змінити значення помилкового біту, нумеруючи біти зліва направо, починаючи з 1.

Приклад 2 Повідомлення кодується (4, 7)- кодом Хеммінга. Декодуємо прийняту послідовність y=(0011111).

Обчислюємо синдром прийнятого вектора:

y = (0011111) = (011)₂ =3₁₀ - помилка виникла у 3-му біті.

Виправляємо помилку, змінюючи значення у помилковому біті: (0011111) (0001111).

Передане повідомлення декодується так:

D(u₁, u₂, u₃, u₄, u₅, u₆, u₇)=D(0001111)=(0111).

Твірна матриця (k, n)-коду Хеммінга - це матриця (k×n), в якій стовпці з номерами нестепеня 2 утворюють одиничну підматрицю, а решта стовпців визначається з перевірних рівнянь коду. Така матриця при кодуванні копіюватиме біти повідомлення у позиції з номерами нестепеня 2 і заповнюватиме інші позиції коду згідно з перевірним рівнянням знаходження відповідного контрольного розряду.

Приклад 3 Система перевірних рівнянь (4, 7)- коду Хеммінга має вигляд:

r₁= u₁ = u₃+u₅+u₇ = m₁+m₂+m_4,

r₂= u₂ = u₃+u₆+u₇ = m₁+m₃+m₄,

r₃= u₄ = u₅+u₆+u₇ = m₂+m₃+m₄.

Відповідно твірна матриця даного коду така:

.

Зразки розв'язування задач до розділу 11

Приклад 1 Закодувати повідомлення 11001010110 двійковим кодом Хеммінга. Побудувати твірну матрицю коду. Навести приклад виправлення помилки і декодування повідомлення. Визначити надлишковість коду.