8.2 Стиснення без втрат інформації

У системах стиснення без втрат декодер відновлює дані джерела абсолютно точно. Узагальнена схема системи стиснення без втрат інформації має такий вигляд (рис. 2.12):

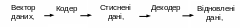
Рисунок 2. 12

Вектор даних, що підлягає стисненню, є послідовністю скінченної довжини. Елементарні повідомлення, що утворюють вектор , обираються із скінченного алфавіту джерела X.

Виходом кодера є стиснені дані у вигляді двійкової послідовності , довжина якої k залежить від . Оскільки система стиснення неруйнуюча, то однаковим векторам відповідають однакові кодові слова на виході кодера .

8.3 Стиснення із втратами інформації

У системах стиснення із втратами інформації кодування здійснюється так, що декодер не в змозі відновити дані джерела в первинному вигляді. Узагальнена схема системи стиснення із втратами інформації зображена на рис. 2.13

Рисунок 2. 13

На відміну від попередньої схеми (рис. 2.12) у цій схемі наявний квантователь, що перетворює вектори вхідних даних на вектор достатньо близький до за значенням середньоквадратичної помилки. Задача квантователя полягає у зменшенні розміру алфавіту джерела. Звичайно, на цьому етапі дані приводять до вигляду, в якому вони можуть бути ефективно стиснуті без втрат.

Далі кодер піддає неруйнуючому стисненню вектор квантованих даних так, щоб забезпечувалася однозначна відповідність між і , тобто для будь-яких виконується умова . Проте система в цілому залишається руйнуючою, оскільки двом різним векторам на вході може відповідати той самий відновлений вектор.

Руйнуючий кодер характеризується швидкістю стиснення R і величиною спотворень D, що знаходяться за формулами:

, . (2.17)

Параметр R характеризує швидкість стиснення у бітах на одне елементарне повідомлення, а параметр D є мірою середньоквадратичної різниці та . Ці два параметри пов'язані зворотною залежністю.

Вибір системи стиснення із втратами або без втрат залежить від типу даних, що стискаються. При стисненні текстів, документів, комп'ютерних програм, банківської інформації і т. ін. очевидно, що необхідно використовувати неруйнуюче стиснення, оскільки в цих випадках необхідне точне відновлення початкової інформації. А у тих випадках, коли інформація, що стискається, використовується лише для якісної її оцінки - це, як правило, аналогові дані, використовується стиснення із втратами, що виявляється дуже доцільним, оскільки при практично непомітних спотвореннях стиснення із втратами забезпечує на порядок, а іноді і на два більшу його швидкість. Зрозуміло, що стиснення із втратами забезпечує і істотно більший коефіцієнт стиснення порівняно із системами неруйнуючого кодування.

Контрольні запитання до розділів 3-8

1. Що таке економне кодування інформації? З якою метою воно здійснюється?

2. Які існують способи задання кодів?

3. Що таке рівномірні й нерівномірні коди?

4. З якою метою використовуються оптимальні нерівномірні коди?

5. Що таке надлишковість коду? Як вона визначається?

6. Яке кодування інформації називається статистичним? Які алгоритми стиснення даних відносять до статистичних?

7. Що таке оптимальне кодування інформації? Який критерій оптимальності статистичних кодів?

8. Які коди називаються префіксними? Що таке вектор Крафта? Як записується нерівність Крафта? У чому полягає умова оптимальності префіксних кодів?

9. У чому полягає алгоритм побудови птимального коду Шеннона-Фано?

10. У чому полягає алгоритм побудови оптимального коду Хаффмена?

11. Які переваги та недоліки використання оптимального кодування Шеннона-Фано і Хаффмена?

12. Чим визначається верхня границя стиснення інформації? Які існують границі стиснення при використанні оптимального кодування Шеннона-Фано і Хаффмена?

13. Які коди характеризуються «наявністю пам'яті»?

14. Які коди називаються блоковими? Що таке порядок блокового коду?

15. У чому полягає метод блокування повідомлень? Як будується блоковий код Хаффмена?

16. У чому полягає арифметичний алгоритм кодування інформації? Які його переваги в порівнянні з іншими статистичними методами стиснення інформації?

17. Як здійснюється декодування даних за арифметичним алгоритмом?

18. У чому полягає адаптивний алгоритм Хаффмена? Що таке упорядковане дерево Хаффмена?

19. Як здійснюється кодування/декодування вхідних даних за адаптивним алгоритмом Хаффмена?

20. Які переваги і недоліки адаптивного алгоритму Хаффмена?

21. У чому полягає основна ідея словникових методів стиснення інформації? У чому переваги використання словникових методів у порівнянні із статистичними?

22. На які основні групи поділяються словникові алгоритми стиснення? Які їх відмітні риси?

23. У чому полягають словникові методи стиснення з використанням «ковзного» вікна LZ77, LZSS? Чим визначається довжина кодів цих алгоритмів?

24. Які переваги модифікованого алгоритму LZSS у порівнянні з LZ77?

25. Які недоліки словникових алгоритмів LZ77, LZSS?

26. У чому полягають словникові методи стиснення LZ78, LZW? Чим визначається довжина кодів для цих алгоритмів? Які переваги модифікації LZW?

27. Які переваги алгоритмів LZ78, LZW у порівнянні з LZ77, LZSS?

28. Які основні елементи включає система стиснення інформації? Які функції вони виконують?

29. За якими ознаками класифікують системи й методи стиснення даних?

30. Чим відрізняються системи стиснення інформації, призначені для передачі й для архівації даних?

31. Які способи стиснення належать до лінійних, матричних, каскадних?

32. Як характеризуються системи стиснення інформації за ступенем і швидкістю стиснення?

33. Як знаходяться коефіцієнт та швидкість стиснення двійкових даних?

34. Які системи характеризуються стисненням без втрат інформації? Які основні елементи вони включають?

35. Які системи характеризуються стисненням із втратами інформації? У чому різниця систем із втратами й без втрат інформації?

36. Чим визначаються швидкість стиснення й величина спотворень у системах стиснення із втратами інформації?

Частина III Завадостійке кодування інформації

Розділ 9 ОСНОВНІ ПРИНЦИПИ ЗАВАДОСТІЙКОГО КОДУВАННЯ.

ЛІНІЙНІ БЛОКОВІ КОДИ