Розв'язання

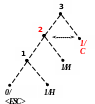
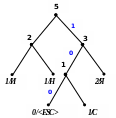
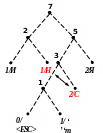
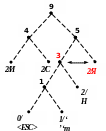
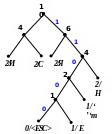
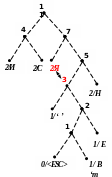
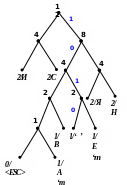
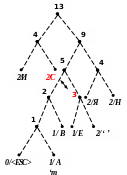
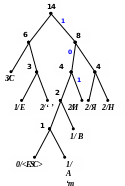
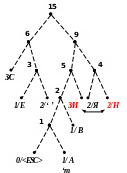
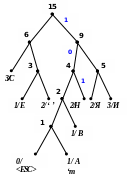
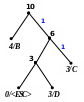
Процес кодування повідомлення і відповідні зміни кодового дерева подаються в табл. 1 і на рис. 1.

Т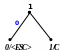 аблиця 1

Вхідні дані	Код	Довжина Коду	Номер дерева
С	‘C’	8	1
И	0‘И’	9	2
Н	00‘Н’	10	3
Я	100‘Я’	11	4
Я	001	3	5
	100‘  ’	11	6
С	101	3	7
И	00	2	8
Н	101	3	9
Е	1100‘Е’	12	10
В	11000‘В’	13	11
А	10100‘А’	13	12
	1010	4	13
С	101	3	14
И	101	3	15
Н	101	3	16
И	111	3

1)

2 )

3)

4

0/<ESC>

)

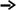
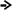
5 )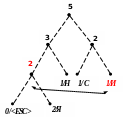

6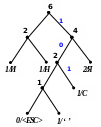 ) 7)

8)

9)

1 0) 11)

12)

1 3)

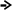
14)

15)

16)

Рисунок 1

Довжина коду стиснутого повідомлення L(X)=114 (бітів).

Довжина ASCII+коду нестиснутого повідомлення L(X)=136(бітів).

Приклад 2 Розпакувати повідомлення ‘B’0‘D’00‘C’11111 110101011011110100101, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжину стиснутого і нестиснутого повідомлення у бітах.

Розв'язання

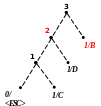
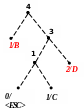
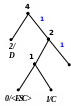
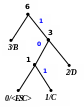
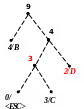
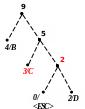
Процес декодування ілюструється таблицею 1, відповідні зміни кодового дерева – рис. 1.

Т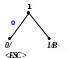 аблиця 1

Вхідний код	Символ	Довжина Коду	Номер дерева
‘B’	B	8	1
0‘D’	D	9	2
00‘C’	C	10	3
11	D	2	4
11	B	2	5
11	B	2	6
101	C	3	7
0	B	1	8
101	C	3	9
101	D	3	10
11	C	2	11
101	D	3	12
0	B	1	13
0	B	1	14
101	D	3
=53

1)

2)

3) 4)

5) 6)

7) 8)

9 )

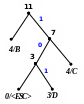10) 11)

12) 13) 14)

Рисунок 1

Отже, закодоване повідомлення BDCDBBCBCDCDBBD.

Довжина стиснутого повідомлення L(X)=53 (біти).

Довжина нестиснутого повідомлення в коді ASCII+

L(X)=158=120 (бітів).

Задачі до розділу 6

1. Закодувати повідомлення AABCDAACCCCDBB за адаптивним алгоритмом Хаффмена. Обчислити довжину у бітах стиснутого повідомлення і його ASCII+-коду.

2. Закодувати повідомлення КИБЕРНЕТИКИ за адаптивним алгоритмом Хаффмена. Обчислити довжини в бітах стиснутого повідомлення і його ASCII+- коду.

3. Розкодувати повідомлення ‘A’0‘F’00‘X’01111101010110111101 00101, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.

4. Розкодувати повідомлення ‘D’0‘B’0100‘C’000‘A’11010 11111110, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.

5. Закодувати повідомлення МАТЕМАТИКА за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.

6. Розкодувати повідомлення ‘B’0‘D’00‘C’01111101010110111101 00101, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.

7. Розкодувати повідомлення ‘К’0‘Р’00‘А’100‘С’000‘Н’011100‘Я’ 0100‘  ’1100101001011110, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.

8. Закодувати повідомлення ПРОГРАММА за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.

9. Закодувати повідомлення ТЕОРИЯ ИНФОРМАЦИИ за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.

10. Розкодувати повідомлення ‘В’0‘О’00‘  ’100‘Д’1010000‘Р’0100‘Е’ 01011001010010000‘Н’10000‘И’111100‘К’, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.

11. Розкодувати повідомлення ‘X’0‘F’00‘Z’1111101100‘A’11101011, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.

Розділ 7 СЛОВНИКОВІ МЕТОДИ СТИСНЕННЯ ЗІВА-ЛЕМПЕЛА

Раніше нами розглядалися статистичні методи стиснення інформації. Словникові алгоритми мають менш математичне обґрунтування, але більш практичний характер. Майже усі словникові методи розроблені ізраїльськими вченими Якобом Зівом (Ziv) та Абрамом Лемпелем (Lempel) і були вперше опубліковані у 1977 році.

Суть словникових методів полягає в тому, що повторювані підрядки у повідомленні замінюються покажчиками на місце у повідомленні, де ці підрядки вже раніше з'являлися. Декодування стиснутого повідомлення здійснюється заміною покажчика готовою фразою із словника, на яку цей покажчик вказує. LZ-методи забезпечують високий степінь стиснення даних, і їхньою важливою перевагою є швидка робота декодера.

Всі словникові методи можна поділити на дві групи.

До першої групи належать алгоритми з використанням «ковзного» за повідомленням вікна, розділеного на дві нерівні за об'ємом частини: перша, більша за розміром, включає фрагмент повідомлення, що вже проглянуто, – ця частина використовується як словник, друга частина вікна, набагато менша, виступає як буфер, що містить ще незакодовані символи вхідного потоку. Звичайно розмір ковзного вікна займає декілька кілобайтів, а розмір буфера - не більше 100 байтів. Алгоритми цієї групи відшукують у словнику (більшій частині вікна) ланцюжки символів, що збігаються із вмістом буфера, і замінюють ці ланцюжки покажчиками на їхнє попереднє входження у повідомлення, тобто на вміст словника. Словник в неявному вигляді міститься у закодованих даних, а зберігаються покажчики на повторювані ланцюжки символів (підрядки), що зустрічаються у повідомленні.

Усі алгоритми першої групи словникових методів базуються на алгоритмі, що має назву за іменами його авторів і роком розроблення – LZ77. Найдосконаліший представник цієї групи –алгоритм LZSS, опублікований у 1982 році Сторером (Storer) та Шиманські (Szimanski).

Алгоритми другої групи доповнюють початковий словник джерела словником фраз, що є повторюваними у повідомленні комбінаціями символів початкового словника. При цьому розмір словника збільшується, і для його кодування потрібне більше число бітів, але значна частина словника представлятиме вже не окремі букви, а сполучення букв або цілі слова. Якщо кодер знаходить фразу, що раніше зустрічалася, він замінює її індексом цієї фрази у словнику. При цьому довжина коду індексу виходить менше або набагато менше довжини коду незакодованого підрядка.

Базовий алгоритм другої групи словникових методів – алгоритм LZ78, розроблений Зівом і Лемпелем у 1978 році. Найдосконаліший представник цієї групи словникових методів – алгоритм LZW, запропонований у 1984 році Тері Уелчем.