Розв'язання

Заданий арифметичний код повідомлення 010001011 – це 9-розрядна двійкова комбінація, що визначає число, яке належить відрізку закодованого повідомлення.

Знайдемо це число: 010001011₂ = 139₁₀.

Число є поточним кодом повідомлення. Воно належить інтервалу, який визначає перший символ повідомлення 0,272  [1/4; 3/4) - це інтервал символу «В».

Щоб знайти наступне значення поточного коду, потрібно від попереднього його значення відняти нижню границю інтервалу розкодованого символу і різницю розділити на ширину цього інтервалу. Отримуємо число, що належить відрізку наступного символу і т.д.

Процес розкодування повідомлення такий:

Поточний код повідомлення	Символ	Інтервал	Ширина інтервалу
0,272	B	[1/4; 3/4)	1/2
=0,043	A	[0; 1/4)	1/4
=0,172	A	[0; 1/4)	1/4
=0,688	B	[1/4; 3/4)	1/2
=0,876	C	[3/4; 1)	1/4

Розкодування повідомлення потрібно закінчити після отримання 5-го символу.

Таким чином, закодовано повідомлення BAABC.

Задачі до розділу 5

1. Побудувати таблиці кодів і обчислити їх середню довжину за алгоритмами Шеннона-Фано, Хаффмена і арифметичним для дискретної випадкової величини Х, заданої таким розподілом:

   X	1	4	9	16	25	36	49	.
   P	0,1	0,1	0,1	0,3	0,1	0,1	0,2

2. Обчислити середню довжину кодів Шеннона-Фано, Хаффмена і арифметичного для значень дискретної випадкової величини Х, заданої таким розподілом ймовірностей:

   X	-2	-1	0	1	2	.
   P	1/3	1/4	1/5	1/6	1/20

3. Обчислити середню довжину кодів Шеннона-Фано, Хаффмена і арифметичного для значень дискретної випадкової величини Х, заданої таким розподілом ймовірностей:

   X	1	2	3	4	5	6	7	8	.
   P	0,1	0,2	0,1	0,05	0,1	0,05	0,3	0,1

4. Побудувати таблиці кодів і обчислити їх середню довжину за алгоритмами Шеннона-Фано, Хаффмена і арифметичним для дискретної випадкової величини Х, заданої таким розподілом:

   X	1	2	3	4	5	6	.
   P	0,4	0,2	0,05	0,05	0,2	0,1

5. Побудувати коди Шеннона-Фано, Хаффмена, арифметичний для повідомлення ABAAAB. Обчислити їх довжину. Приблизний закон розподілу ймовірностей символів визначити з аналізу повідомлення.

6. Закодувати за арифметичним алгоритмом повідомлення BAABC дискретної випадкової величини X, заданої таким розподілом ймовірностей: P(X=A)=1/3, P(X=B)=7/15, P(X=C)=1/5. Обчислити довжину коду.

7. Побудувати арифметичний код для повідомлення AFXAFF. Обчислити його довжину. Приблизний закон розподілу ймовірностей символів визначити з аналізу повідомлення.

8. Розпакувати повідомлення довжиною 6 символів, закодоване за арифметичним алгоритмом. Код повідомлення 101000001. Таблиця кодера така:

   Символ	Інтервал
   A	[2/3; 1)
   B	[1/5; 2/3)
   C	[0; 1/5)

9. Розпакувати повідомлення, закодоване за арифметичним алгоритмом. Кінець повідомлення відмічений маркером . Код повідомлення 010101. Таблиця символів і інтервалів така:

   Символ	Інтервал
   	[5/6; 1)
   A	[2/3; 5/6)
   B	[0; 2/3)

10. Розпакувати повідомлення з 5 символів, закодоване за арифметичним алгоритмом. Код повідомлення 011110101. Таблиця символів і інтервалів така:

    Символ	Інтервал
    A	[3/4; 1)
    C	[1/2; 3/4)
    B	[0; 1/2)

11. Для кодування послідовностей довжиною 6 символів двійкового джерела, імовірність одиниці в якому 1/6, використовується арифметичний алгоритм. Таблиця кодера така:

Символ	Інтервал
1	[5/6; 1)
0	[0; 5/6)

Знайти відповідні незакодовані вхідні послідовності, якщо кодові слова на виході кодера такі: а) 10000; б) 01011; в)10111.

Розділ 6 АДАПТИВНИЙ АЛГОРИТМ ХАФФМЕНА З УПОРЯДКОВАНИМ ДЕРЕВОМ

На відміну від раніше розглянутих методів стиснення адаптивний (динамічний) алгоритм Хаффмена більш практичний, однопрохідний, не потребуючий передачі таблиці кодів. У процесі кодування залежно від значення поточного символу, що надходять на вхід алгоритму, кодове дерево постійно змінюється – коригується відповідно до зміни статистики вхідного потоку. При декодуванні відбувається той самий процес. Для однозначності декодування використовується упорядкована структура кодового дерева.

Упорядкованим деревом Хаффмена називається бінарне дерево, вузли якого можуть бути перелічені у порядку неубування їх ваги зліва-направо на кожному рівні і знизу-вверх за рівнями. Якщо дерево упорядковано таким чином, то при зміні ваги існуючого вузла в дереві достатньо поміняти місцями два вузли: вузол, що порушив упорядкованість, і останній з наступних за ним вузлів меншої ваги. Після обміну вузлів місцями необхідно перерахувати вагу всіх вузлів-предків.

На початку роботи алгоритму дерево містить тільки один спеціальний символ <ESC>, що завжди має частоту 0. Він необхідний для занесення в кодове дерево нового символу, що передається безпосередньо після <ESC>. При появі нового символу праворуч від вузла <ESC> додається лист і потім, якщо необхідно, дерево упорядковується. Ліві гілки кодового дерева позначаються 0, а праві - 1.

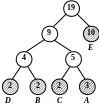
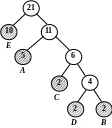
Наведемо приклад впорядкованого таким чином дерева Хаффмена (рис. 2.8 а). Додамо в це дерево дві букви «А», тоді вузли «A» і «D» повинні помінятися місцями (рис. 2.8 б). Якщо додати ще дві букви «А», то потрібно поміняти місцями спочатку вузол «А» та вузол - батько «D» і «В», а потім вузол «Е» і вузол - брат «Е» (рис. 2.8 в-г).

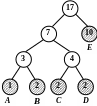
а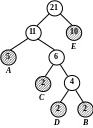 ) б)

в) г)

Рисунок 2. 8

Розглянемо приклади кодування/ декодування повідомлень за адаптивним алгоритмом Хаффмена.

Приклад 1 Побудуємо адаптивний код Хаффмена для повідомлення АССВСАААВС.

Процес кодування цього повідомлення подається табл. 2.11, а відповідні зміни кодового дерева показані на рис. 2.9. Домовимося символом в лапках позначати двійковий восьмибітовий код символу за таблицею ASCII+.

Т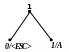 аблиця 2.11

Вхідні дані	Код	Довжина коду	Номер дерева
А	‘A’	8	1
С	0‘C’	9	2
С	01	2	3
В	00‘B’	10	4
С	1	1	5
А	01	2	6
А	01	2	7
А	11	2	8
В	101	3	9
С	11	2
		=41

1)

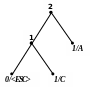
2)

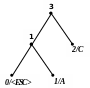
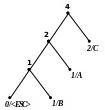
3) 4)

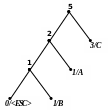
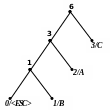
5) 6)

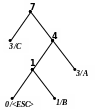
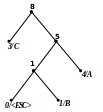7 ) 8)

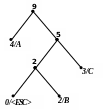
9)

Довжина стиснутого повідомлення

L^{адапт.Хаффмена} = 41 (біт).

Довжина стиснутого повідомлення у коді

ASCII+ L^ASCII+ =80 (бітів).

Рисунок 2. 9

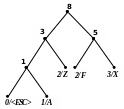
Приклад 2 Розкодуємо повідомлення ‘X’0‘F’00‘Z’1111101 100‘A’111010, закодоване за адаптивним алгоритмом Хаффмена. Обчислимо довжини кодів стиснутого та нестиснутого (ASCII+) повідомлень.

Процес декодування ілюструється табл. 2.12 і рис. 2.10.

Т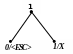 аблиця 2.12

Код	Символ	Довжина Коду	Номер дерева
‘X’	X	8	1

1)

0‘F’

F

9

2

П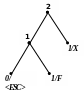 родовження табл. 2.12

Код	Символ	Довжина Коду	Номер дерева
00‘Z’	Z	10	3
11	F	2	4
11	X	2	5
101	Z	3	6
100‘A’	A	11	7
11	X	2	8
10	F	2	9
10	F	2
		=51

2)

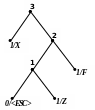
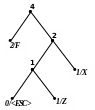
3) 4)

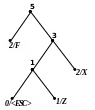
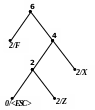
5) 6)

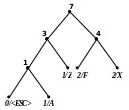
7 ) 8)

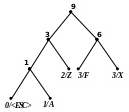
9)

Довжина стиснутого повідомлення

L^{адапт.Хаффмена} =51 (біт).

Довжина нестиснутого повідомлення у коді ASCII+ L^ASCII+=80 (бітів).

Рисунок 2. 10

На практиці адаптивний алгоритм Хаффмена забезпечує високий ефект стиснення, оскільки він враховує локальні зміни ймовірностей символів у вхідному потоці. Цей алгоритм характеризується мінімальною надмірністю за умови кодування кожного символу повідомлення не менш ніж одним бітом інформації. До недоліків цього алгоритму так само, як для неадаптивних оптимальних алгоритмів, належить залежність ефекту стиснення від близькості ймовірностей символів значенням від'ємного степеня 2, що пов'язано з необхідністю округлення довжини кожної кодової комбінації до більшого цілого, оскільки кожний символ кодується цілим числом бітів. Тому адаптивний алгоритм Хаффмена у більшості випадків поступається арифметичному методу за рівнем стиснення даних.

Зразки розв'язування задач до розділу 6

Приклад  1 Закодувати повідомлення СИНЯЯ СИНЕВА  СИНИ за адаптивним алгоритмом Хаффмена. Обчислити довжини коду.