4.1 Теоретичні границі стиснення інформації

Стиснення даних не може бути більше деякої теоретичної границі. Сформульована раніше теорема Шеннона про кодування каналу без шуму встановлює верхню границю стиснення інформації як ентропію джерела H(X).

Позначимо через L(X) функцію, що повертає довжину коду повідомлень

L(X)=len(code(X)),

де code(X) кожному значенню X ставить у відповідність деякий бітовий код; len( ) - повертає довжину цього коду.

Оскільки L(X) - функція від д. в. в. X, тобто також є д. в. в., то її середнє значення обчислюється як математичне сподівання:

. (2.3)

Наслідком теореми Шеннона про кодування джерела у відсутності шуму є те, що середня кількість бітів коду, що припадає на одне значення д. в. в., не може бути менше її ентропії, тобто

(2.4)

для будь-якої д. в. в. X і будь-якого її коду.

Нехай - вектор даних завдовжки n; - вектор частот символів у .

Тоді середня кількість бітів коду на одиницю повідомлення обчислюється так:

, (2.5)

де - довжина коду повідомлення : ; - вектор Крафта для .

Ентропія повідомлення обчислюється так:

. (2.6)

Розглянемо функцію y=ln(x), яка є опуклою вниз, тобто її графік лежить не вище своєї дотичної y=x-1. Тоді можна записати таку нерівність:

ln(x)  x-1, x>0. (2.7)

Підставимо в (2.7) і помножимо обидві частини цієї нерівності на :

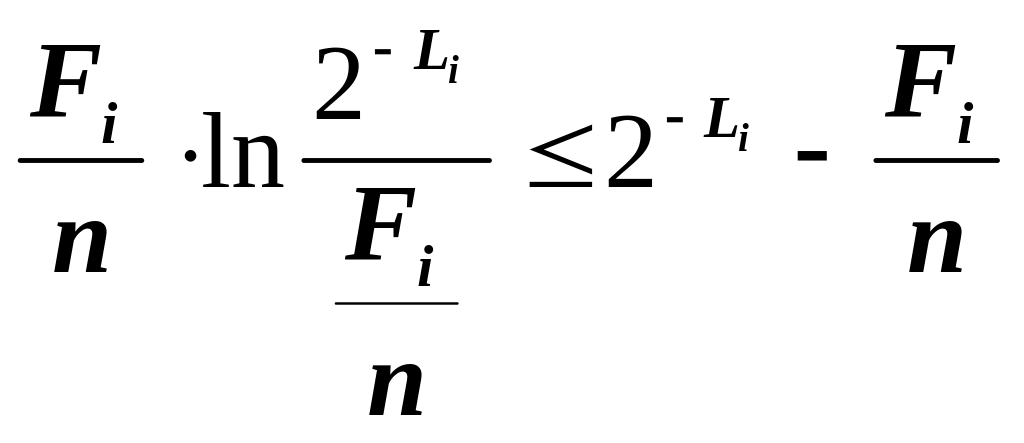. (2.8)

Запишемо суми за i обох частин нерівності (2.8), і з урахуванням того, що для оптимального кодування Хаффмена нерівність Крафта (2.1) переходить в строгу рівність, дістанемо в правій частині (2.8) нуль, отже,

.

Перейдемо від натурального логарифма до двійкового і з урахуванням виразу (2.6) дістанемо

,

тобто приходимо до виразу (2.4), що визначає верхню границю стиснення даних.

Припустимо, що у векторі Крафта довжини кодових слів пов'язані з частотами символів у повідомленні так:

.

При виконанні цієї умови нерівність Крафта (2.1) обертається у строгу рівність, і код буде компактним, тобто матиме найменшу середню довжину. Тоді, оскільки для оптимальних кодів Шеннона-Фано і Хаффмена довжина кожної кодової комбінації округлюється до більшої цілої кількості бітів, маємо

,

звідси

.

Таким чином, границі стиснення інформації при оптимальному статистичному кодуванні визначаються так:

. (2.9)

4.2 Метод блокування повідомлення

На відміну від раніше розглянутих методів кодування блокові коди належать до так званих кодів з пам'яттю, оскільки при кодуванні поточного символу враховуються значення одного або декількох попередніх символів.

Блоковий код розділяє вектор даних на блоки певної довжини, і потім кожний блок замінює кодовим словом з префіксної множини кодових слів. Отриману послідовність кодових слів об'єднують в остаточну двійкову послідовність на виході кодера.

Блоковий код називається блоковим кодом k-го порядку, якщо всі його блоки мають довжину k символів.

Метод блокування повідомлень полягає в такому.

За заданим >0 можемо знайти таке k, що якщо розбити повідомлення на блоки завдовжки k (всього буде n/k блоків), то, використовуючи оптимальне статистичне кодування таких блоків, що розглядаються як одиниці повідомлень, можна досягти середньої довжини коду більше ентропії менш ніж на .

Припустимо, що X₁, X₂, …, X_n – незалежні д. в. в., що мають однаковий розподіл ймовірностей. Тоді ентропія n-вимірної д. в. в.

.

Нехай - повідомлення джерела, де , , … , - блоки повідомлення. Тоді

. (2.10)

При оптимальному кодуванні k-послідовностей векторної д. в. в. , що розглядаються як одиниці повідомлення, справедлива нерівність

. (2.11)

Середня кількість бітів на одиницю повідомлення X

. (2.12)

Тоді з урахуванням (2.10) і (2.12) нерівність (2.11) можна записати так:

. (2.13)

Розділивши обидві частини (2.13) на k, отримуємо

, (2.14)

тобто достатньо вибрати .

Приклад 1 Стиснемо вектор даних X=(0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1), використовуючи блоковий код 2-го порядку.

Розіб'ємо вектор на блоки довжини 2: (01, 10, 10, 01, 11, 10, 01, 01). Розглядатимемо ці блоки як елементи нового алфавіту {01, 10, 11}. Визначимо вектор частот появи блокових елементів в заданій послідовності. Одержуємо (4, 3, 1), тобто найбільш часто трапляється блок 01, потім 10 і найменше - 11; всього 8 блоків. Код Хаффмена для блоків символів представимо у вигляді кодового дерева (рис. 2) і відповідної таблиці кодів (табл. 2.5).

Таблиця 2.5

Блок повідомлення	Кодове слово
01	0
10	10
11	11

Замінюючи кожний блок повідомлення відповідним кодовим словом з таблиці кодів, дістанемо вихідну кодову послідовність Code(01, 10, 10, 01, 11, 10, 01, 01)= 010100111000.

Обчислимо ентропію, використовуючи статистичний розподіл ймовірностей символів повідомлення:

 (біт/сим).

Швидкість стиснення даних (середня довжина коду)

 (біт/сим).

Отриманий результат виявляється меншим за ентропію, що, здавалося, суперечить теоремі Шеннона. Проте це не так. Легко бачити з вектора початкових даних, що символ 0 частіше слідує 1, тобто умовна імовірність p(1/0) більше безумовної p(1). Отже, ентропію цього джерела необхідно обчислювати як ентропію статистично взаємозалежних елементів повідомлення, а вона менша за безумовну.

Приклад 2 Нехай д. в. в. X₁, X₂, …, X_n незалежні, однаково розподілені і можуть набувати тільки два значення 0 та 1 з такою ймовірністю: P(X_i=0)=3/4 та P(X_i=1)=1/4, i=1…n.

Тоді ентропія одиниці повідомлення

 (біт/сим).

Мінімальне префіксне кодування - це коди 0 або 1 завдовжки 1 біт. Отже, середня кількість бітів на одиницю повідомлення  (біт/сим).

Розіб'ємо повідомлення на блоки довжиною n=2. Закон розподілу ймовірностей і відповідне кодування двовимірної д. в. в. наведені у табл. 2.6.

Таблиця 2.6

	00	01	10	11
P	9/16	3/16	3/16	1/16
Префікс ний код	0	10	110	111
	1	2	3	3

У цьому випадку середня кількість бітів на одиницю повідомлення =(19/16+23/16+33/16)/2=27/32

0,84375 (біт/сим), тобто менше, ніж для неблокового коду.

Для блоків довжини три середня кількість бітів на одиницю повідомлення ≈0,823, для блоків довжини чотири – ≈0,818 і т. д.

Додамо, що формули теоретичних границь стиснення задають границі для середньої довжини коду на одиницю повідомлення – на окремих же повідомленнях степінь стиснення даних може бути меншим за ентропію.

Зразки розв'язування задач до розділу 4

Приклад 1 Дискретна випадкова величина (д. в. в.) X задана таким розподілом ймовірностей: P(X=A)=1/3; P(X=B)=7/15; P(X=C)=1/5. Побудувати таблицю кодів для блокового коду Хаффмена 2-го порядку. Визначити середню довжину коду.