ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Мурманский государственный технический университет»

Институт дополнительного профессионального образования (ЦСЭП)

Кафедра менеджмента, коммерции,

маркетинга и рекламы

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Инвестиционный менеджмент»

Выполнил: слушатель гр. МНз 11 .

Иванов Виталий Николаевич

Руководитель:

Белевских Татьяна Васильевна

Работа сдана на кафедру: «___» ________ 2013 г.

Работа проверена: «___» ________ 2013 г.

Мурманск

2013

Задача 1. По способу равномерного начисления износа рассчитайте ежегодную сумму начисленного износа для единицы оборудования со сроком службы 10 лет, первоначальной стоимостью 14 млн. руб. и ликвидационной стоимостью 1,7 млн. руб.

Решение:

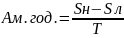
Ам.год. – сумма ежегодного износа (амортизация)

Sн – первоначальная стоимость

Sл – ликвидационная стоимость

T – срок службы оборудования

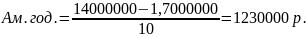
Ответ: ежегодная сумма начисленного износа составляет 1230000 р.

Задача 2. Пусть номинальная ставка процента с учетом инфляции составляет 35%, а ожидаемый темп инфляции в год 20%. Необходимо определить реальную будущую стоимость объема инвестиций 500 000 руб. через 3 года.

Решение:

1. Определяем реальную ставку

r_н = (1+ r_р)×(1+I) – 1, где

r_н - номинальная ставка процента

r_р - номинальная ставка процента

I - темп инфляции

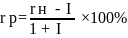
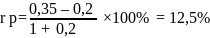
2. Определяем реальную будущую стоимость объема инвестиций

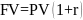³ , где

FV – будущая стоимость

PV – настоящая сумма (вклад)

t – число лет вклада

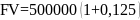³ = 711914,1 р.

Ответ: будущая стоимость объема инвестиций составит 711914,1 р.

Задача 3. Какова процентная ставка (по методу простых процентов) вклада в 750 тыс. рублей через 5 лет, если его будущая стоимость составляет 2,1 млн. руб.

Решение:

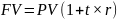, где:

FV – будущая стоимость

PV – настоящая сумма (вклад)

t – число лет вклада

r – ставка в процентах

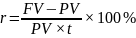
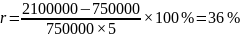
Ответ: процентная ставка равна 36 %

Задача 4. Вам предлагают инвестировать деньги с гарантией утроить их количество через три года. Какова процентная ставка прибыльности такой инвестиции (по методу сложных процентов)?

Решение:

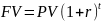, где

FV – будущая сумма

PV – настоящая сумма

t – число лет вклада

r – ставка в процентах

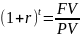
r =

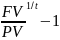
Поскольку будущее значение какой-либо суммы FV относится к настоящему значению PV как 3:1, то

r = (3^1/3 -1) = 0,4422×100% = 44,22%

Ответ: процентная ставка равна 44,22%

Задача 5. Первоначальная сумма вложений составляет 300 тыс. рублей. В первой половине года применялась простая процентная ставка r₁=15%, во второй половине – простая процентная ставка r₂=12%. Найти наращенную сумму.

FV = PV(1+t₁r₁+…+t_nr_n), где:

FV – будущая стоимость

PV – настоящая сумма (вклад)

t – период вклада, лет

r – ставка в процентах

Т.к. период поделен пополам, то t₁=t₂=0,5

FV = 300000(1+0,15×0,5+0,12×0,5) = 340500р.

Ответ: наращенная сумма равна 340500р.

Задача 6. Первоначальная сумма вложений в 500 тыс. рублей наращивалась по сложной процентной ставке в 15% в течение 2 лет, затем по ставке 14% годовых в течение 3 лет. Найти наращенную сумму.

FV = PV(1+r₁)^t1×…×(1+r_n)^tn , где

FV – будущая сумма

PV – настоящая сумма

t – число лет вклада

r – ставка в процентах

FV = 500000(1+0,15)² × (1+0,14)³ = 661251,48

Ответ: наращенная сумма равна 661251,48р.

Задача 7. Рассчитайте будущую стоимость 250 000 руб. для следующих ситуаций:

а) 6 лет, 10% годовых, ежегодное начисление процентов; б) 6 лет, 10% годовых, полугодовое начисление процентов; в) 6 лет, 10% годовых, ежеквартальное начисление процентов.

Решение:

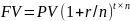, где

FV – будущая сумма

PV – настоящая сумма

t – число лет вклада

n – количество начислений

r – ставка в процентах

а) 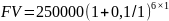= 442890,25р.

б) 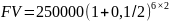= 448964,1р.

в) = 452181,5р.

Ответ: будущая стоимость 250000р. будет стоить

а) при ежегодном начислении процентов - 442890,25р.

б) при полугодовом начислении процентов - 448964,1р.

в) при ежеквартальном начислении процентов - 452181,5р.

Задача 8. Найдите коэффициент приведенной стоимости аннуитета для процентной ставки в 14,86% и восьми лет.

Решение:

Формула приведенной стоимости аннуитета:

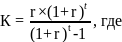
r – ставка в процентах

t – число лет вклада

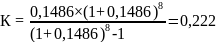
Ответ: коэффициент приведенной стоимости аннуитета равен 0,222

Задача 9. Найдите будущую стоимость пятигодичного простого аннуитета с ежегодной выплатой 3 800 руб. при процентной ставке, равной 9,6% годовых.

Решение:

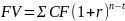, где

FV – будущая сумма

CF- сумма ежегодных поступлений (выплат)

t – число лет вклада (от 1 до 5)

n – количество начислений (всего)

r – ставка в процентах

FV=3800((1+0,096)^5-1 +(1+0,096)^5-2 +(1+0,096)^5-3 +(1+0,096)^5-4 +(1+0,096)^5-5)

FV=23015,34р.

Ответ: будущая стоимость аннуитета составляет 23015,34р.

Задача 10. Четырехгодичный аннуитет в 150 тыс. руб. сегодня стоит 340 тыс. рублей. Какова процентная ставка?

Преобразуем формулу приведенной стоимости таким образом, чтобы выделить процентную ставку:

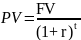
r = (PV/FV)^1/t -1

r = (340/150)^1/4 -1 = 0,227×100% = 22,7%

Ответ: процентная ставка составляет 22,7%

Задача 11. Рассчитайте приведенную и будущую стоимость пятигодичного срочного аннуитета при ставке процента, равной 8% годовых, и ежегодной выплате в 30 тыс. руб.

Решение:

Будущая стоимость аннуитета рассчитывается по формуле:

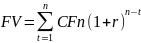, где

FV – будущая сумма

CF- сумма ежегодных поступлений (выплат)

t – число лет вклада (от 1 до 5)

n – количество начислений (всего)

r – ставка в процентах

FV = 30000×((1+0,08)^5-1+(1+0,08)^5-2+(1+0,08)^5-3+(1+0,08)^5-4+(1+0,08)^5-5)

FV = 175998,03 р.

Приведенная стоимость аннуитета рассчитывается по формуле:

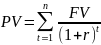
PV = 30000(1/(1+0,08) + 1/(1+0,08)² + 1/(1+0,08)³ +1/(1+0,08)⁴ +1/(1+0,08)⁵)

PV = 119781,3р.

Ответ: будущая стоимость аннуитета составляет 175998,03 р.

приведенная стоимость аннуитета составляет 119781,3 р.

Задача 12. Работник компании надеется, что в течение десяти лет, пока он не уйдет на пенсию, его ежегодная зарплата будет устойчиво прирастать на 10% в год. Его текущая зарплата, которую ему уже выплатили за год, составляет 200 тыс. руб. Если работник может получать 15% на сумму вложения, то какова приведенная стоимость тех средств, которые он получит.

Решение:

1. Величина зарплаты (FV) с учетом ежегодного повышения составит (в тыс. руб.):

PV0	1 год	2 год	3 год	4 год	5 год	6 год	7 год	8 год	9 год	10 год
200	220	242	266,3	292,8	322,1	354,3	389,7	428,7	471,6	518,7

2. Т.к. вклад пополняется в конце каждого года, то конечная сумма за предшествующий год будет начальной суммой следующего года.

По формуле сложных процентов находим cумму средств, полученных за 10 лет:

Выражение (1+r)^t является мультиплицирующим множителем для единичного платежа, и т.к. процентная ставка в течение 10 лет не изменялась, то (1+r)^t = 1,15 (по таблице).

FV= 1,15(200+220+242+266,3+292,8+322,1+354,3+389,7+428,7+471,6)+518,7

FV=3691320р.

3. По формуле 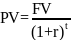находим приведенную стоимость денежных средств, полученных через 10 лет:

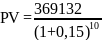= 912437,85 р.

Ответ: приведенная стоимость всех средств составит 912437,85 р.

Задача 13. Пусть выпущена облигация со сроком погашения через 10 лет. Номинал облигации равен 100 000, а годовая процентная ставка, определяющая величину годового процентного платежа, составляет 14 процентов. Средняя процентная ставка на рынке облигаций данного типа составляет также 12%. Необходимо найти оценку стоимости облигации?

Решение: Сущность оценки стоимости облигации состоит в том, что в течение срока существования облигации ее владелец должен получить ту же сумму, которую он вложил в облигацию при покупке. Особенность состоит в том, что совокупность платежей, которые должен получить владелец облигации растянута во времени, и, следовательно, все будущие денежные потоки необходимо продисконтировать к моменту времени, для которого производится оценка стоимости облигации.

Для вычисления приведенной стоимости облигаций (PV) используем формулу:

PV = 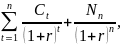где

С_t – сумма ежегодных выплат по облигации

N_n – номинальная стоимость облигации

n - количество периодов (начислений)

t – время до погашения облигации (от 1 до 10)

r – средняя процентная ставка

Cумма ежегодных выплат по облигации

C_t 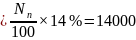р.

PV = 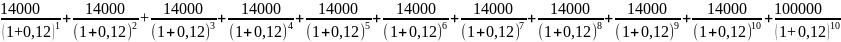= 111300,44 р.

Ответ: облигация оценена в 111300,44 р.

Задача 14. Предприятие в день эмиссии приобрело по цене 7 500 рублей за штуку пакет дисконтных государственных облигаций с периодом обращения 365 дней и номинальной стоимость к погашению 9 000 рублей. Какова доходность финансового инструмента?

Решение:

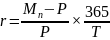
, где

r – доходность

M_n – номинальная стоимость

P – цена облигации

T – число дней до погашения облигации

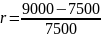
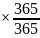= 20%

Ответ: доходность пакета облигаций - 20%

Задача 15. Предприятие выплатило по 30 рублей в виде дивидендов за последний год. В течение ближайших трех лет предприятие планирует увеличивать дивиденды на 8 процентов, а в дальнейшем темп роста дивидендов должен составить 5 процента. Необходимо оценить стоимость акции при условии, что доходность акций оценена на уровне 11%.

Решение:

V_a = V_T+V_T+1=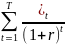 + 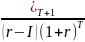, где

V_a – стоимость акций

V_T - стоимость акций до момента T

V_T+1 - стоимость акций после момента T

DIV_t – дивиденд, планируемый к выплате в период t=3года

DIV_t+1 - дивиденд, планируемый к выплате после периода t

r – норма доходности

I – темп роста

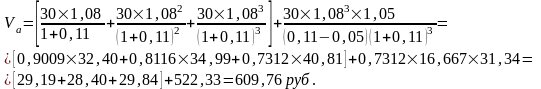
Ответ: стоимость акции составляет 609,76 руб.

Задача 16. Ожидается, что прибыль, дивиденды и рыночная цена акции компании будут иметь ежегодный рост на 7 процентов. В настоящее время акции компании продаются по 400 руб. за штуку, ее последний дивиденд составил 0 руб. и компания выплатит 22 руб. в конце текущего года.

а) Используя модель прогнозируемого роста дивидендов определите стоимость собственного капитала предприятия.

б) Показатель бета для компании составляет 1.5, величина процентной ставки безрискового вложения капитала равна 7%, а средняя по фондовому рынку - 9%. Оцените стоимость собственного капитала компании, используя ценовую модель капитальных активов.

в) Средняя прибыльность на рынке ссудного капитала составляет 9 процентов, и предприятие рассматривает возможную премию за риск в объеме 4 процентов. Какова будет оценка стоимости капитала с помощью модели премии за риск?

г) Сравните полученные оценки. Какую из них следует принять при оценке эффективности инвестиций?