Лабораторная работа №2 Построение и анализ распределения случайной величины по ее выборке

1. Постановка задачи:

Задана выборка экспериментальных значений технологического параметра. Необходимо:

1. Рассчитать среднюю и дисперсию заданной выборки;

2. Определить доверительные интервалы для математического ожидания по критерию Стьюдента, для дисперсии по критерию Пирсона;

3. Построить гистограмму распределения;

4. Сравнить выборочное распределение с теоретическим по критерию Пирсона.

2. Математическое описание и алгоритм решения задачи. Для примера задана экспериментальная выборка параметра x=(1.74, 1.76, 1.6, 1.67, 1.58, 1.79, 1.63, 1.55, 1.69, 1.73, 1.64, 1.75, 1.59, 1.72, 1.83, 1.7, 1.9, 1.65,1.77, 1.66, 1.68)

2.1. Среднее арифметическое и дисперсия для данной выборки рассчитываются по формулам:

. (1.9)

Алгоритм расчета включает в себя циклы накопления двух сумм. Для примера приведем текст программы расчета дисперсии при заданном среднем, составленном в системе VBA.

Sub dispersia()

Dim x(27) As Double

n = 27

sred = 1.68

s2 = 0

For i = 1 To n

x(i) = Cells(i+1, 2)

s2 = s2 + ((x(i) - sred) ^ 2) / (n - 1)

Next i

Cells(30, 2) = "s2"

Cells(31, 2) = s2

End Sub

2.2. Доверительные интервалы определяются для математического ожидания по критерию Стьюдента t_p, а дисперсии - по критерию Пирсона χ², которые определяются по статистическим таблицам по заданным уровне значимости р и числе степеней свободы f.

(1.10)

(1.11)

2.3. Третья задача заключается в построении гистограммы и сравнения выборочного распределения с нормальным. При построении гистограммы диапазон изменения переменной разбивается на определенное количество равных интервалов, затем строится столбиковая диаграмма, по оси абсцисс которой откладываются интервалы переменной с шириной h, а оси ординат – плотность относительной частоты (n_i/n)/h. Гистограмма для приведенных выше исходных данных приведена на рис.3.

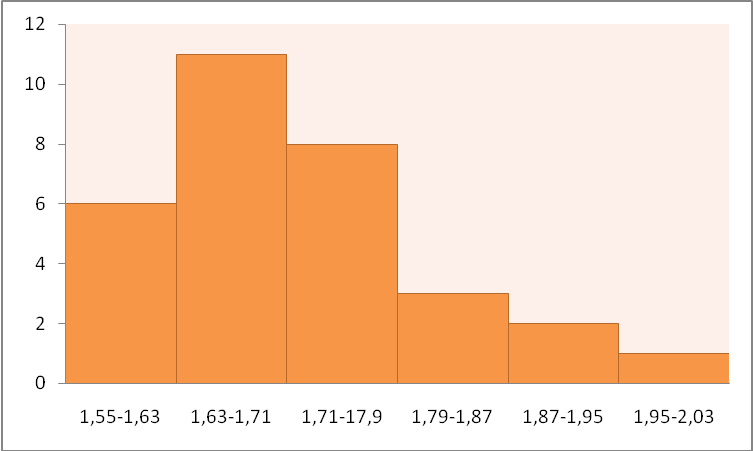
Рис.1.3 Гистограмма распределения

Критерий Пирсона рассчитывается по формуле:

(1.12)

Теоретическая вероятность рассчитывается по функции Лапласа. Для интервала с границами а и b эта вероятность равна

(1.13)

Согласие распределений считается удовлетворительным, если расчетный критерий Пирсона меньше табличного.

Лабораторная работа №3 Построение и анализ уравнения одномерной регрессии

1. Постановка задачи. Исследуется одномерная связь между переменными, получены экспериментальные данные х, у. Необходимо:

1. Рассчитать коэффициенты линейной регрессии и коэффициент корреляции (по программе на алгоритмическом языке);

2. Провести расчеты коэффициентов разных уравнений регрессии с помощью статистического пакета SPSS.

2. Описание задачи. Требуется определить по методу наименьших квадратов коэффициенты линейного уравнения регрессии

(1.14)

по выборке объемом п. Система нормальных уравнений для расчета искомых коэффициентов будет иметь следующий вид:

(1.15)

(1.16)

Из системы уравнений (1.15-1.16) методом подстановки можно получить расчетные формулы для искомых коэффициентов. Коэффициент корреляции рассчитывается по формуле

(1.17)

(1.18) . (1.19)

Алгоритм расчета включает в себя блоки 1) ввода экспериментальных данных, 2) накопления сумм, 3) расчета коэффициентов, 4) расчета коэффициента корреляции.

3. Индивидуальное задание включает в себя массив экспериментальных данных. Студент должен разработать алгоритм расчета и составить программу. По результатам расчета необходимо построить график искомой зависимости.