4.4 Турбулентний рух рідини

4.4.1 Структура турбулентного руху в трубі

При турбулентному русі рідина перемішується, виникають пульсації тиску, а швидкості окремих частинок рідини змінюється з часом за величиною і напрямком.

Рисунок 4. 6 - Коливання швидкості при турбулентному режимі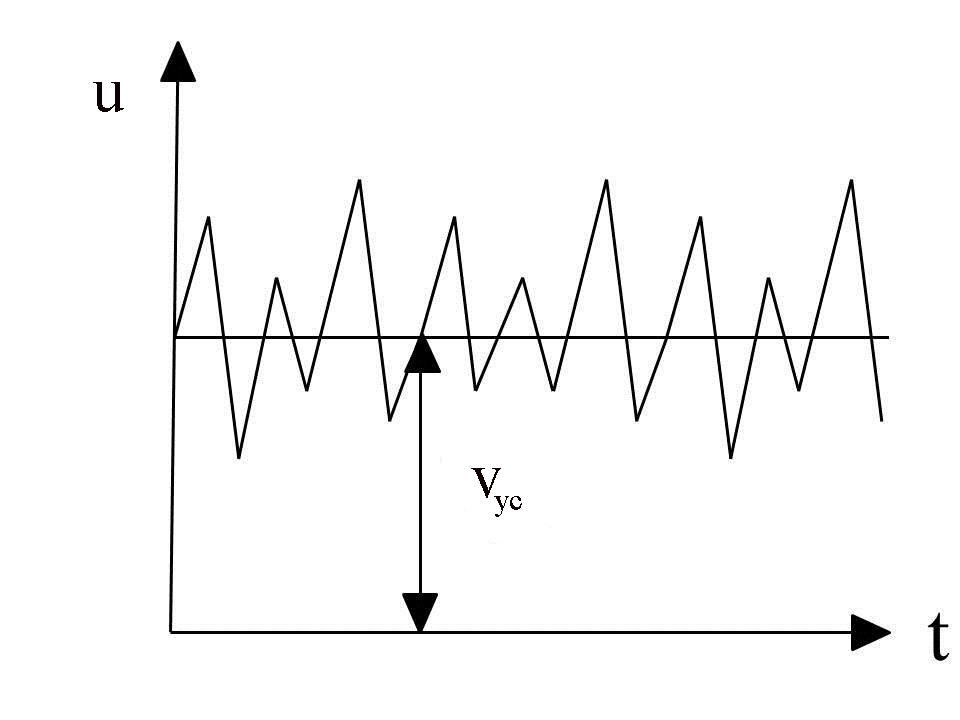

Місцева миттєва швидкість u окремої частинки з часом коливається навколо деякого середнього значення – осередненої швидкості V_ос (рис.4.6). Тобто турбулентний рух завжди є неусталеним, тому що швидкості і тиск, а також траєкторія частинок рідини змінюється з часом. Однак його можна розглядати усталеним за умови, якщо місцева швидкість буде дорівнювати осередненій :

(4.25)

де u – миттєва швидкість.

Розглянемо структуру потоку при турбулентному русі рідини (рис.4.7). Вона відрізняється від ламінарного руху.

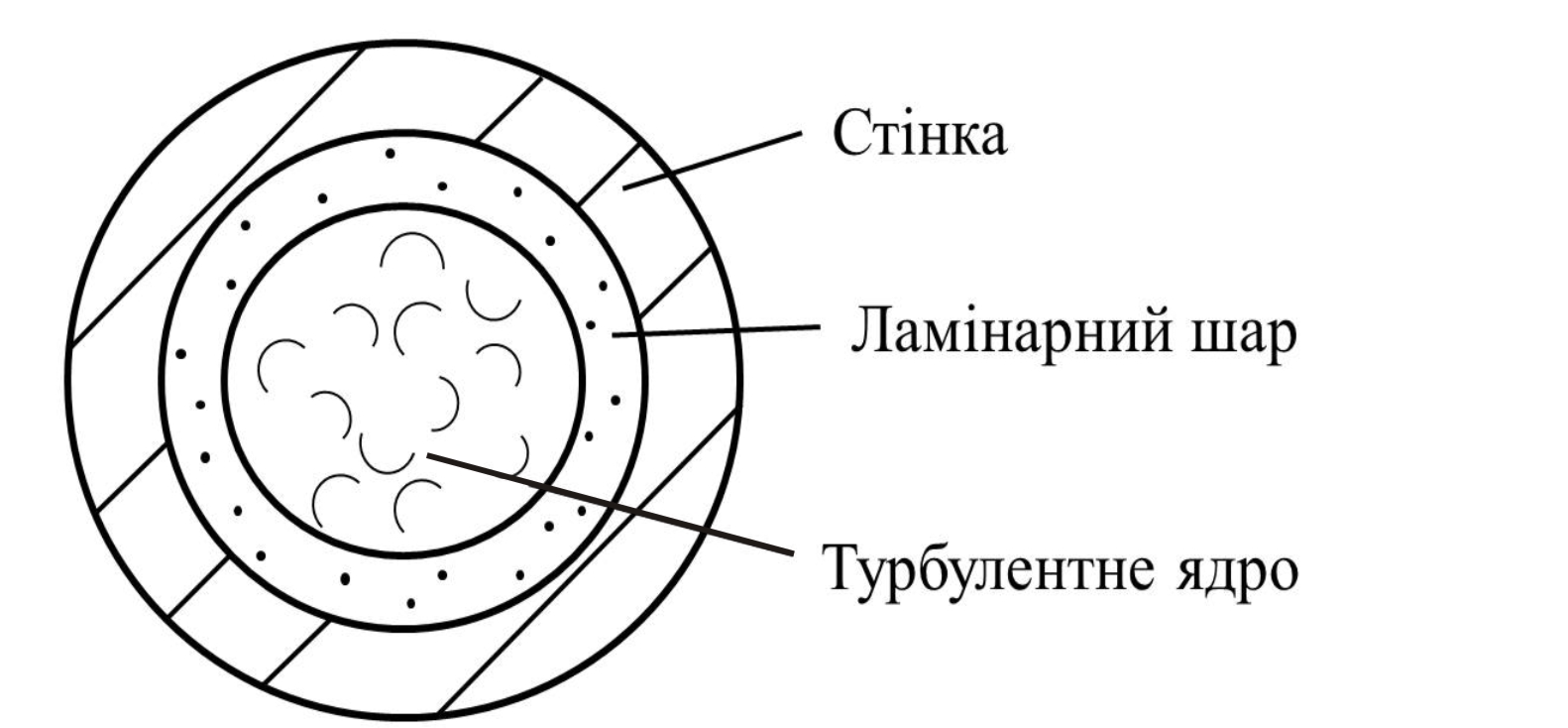
Рисунок 4.7 - Структура потоку в перерізі труби при турбулентному режимі

Якщо розглянути поперечний переріз потоку в трубі, то біля стінки має місце дуже тонкий ламінарний шар, а після невеликої перехідної зони утворюється турбулентне ядро потоку.

Ламінарний шар дуже тонкий і має товщину від 0,1 мм до декількох міліметрів, а всю іншу частину площі живого перерізу займає турбулентне ядро, у якому режим руху турбулентний.

Розподіл швидкостей у поперечному перерізі турбулентного потоку (рис. 4.8) інший, ніж при ламінарному.

П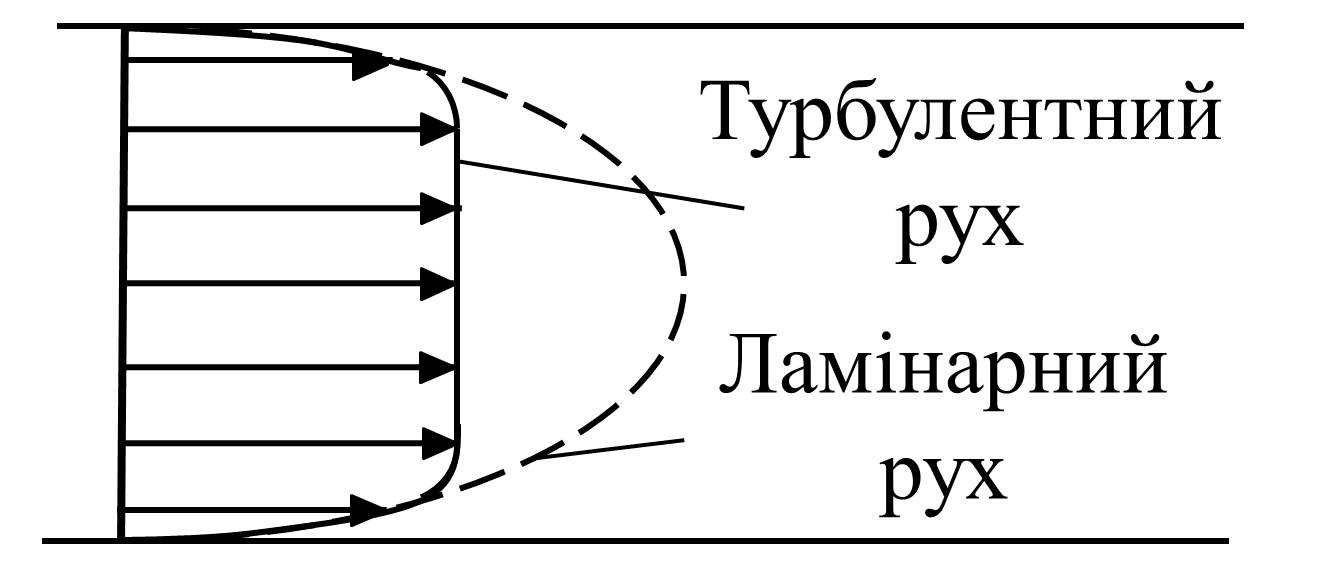 ри турбулентному русі він більш рівномірний, а нарощування швидкості біля стінок буде більш крутим. Коефіцієнт Коріоліса α для турбулентного потоку менший, ніж для ламінарного. Він залежить від числа Рейнольдса:

ля Re = 4000 α = 1,13;

д

Рисунок 4. 8 - Розподіл швидкостей у поперечному перерізі труби

ля Re = 3∙10⁶ α = 1,025.

Для практичних обчислень можна взяти α = 1.

4.4.2 Втрати напору на тертя в трубах. Формула Дарсі-Вейсбаха

П

Рисунок 4.9 - Залежність втрат напору на тертя від швидкості рідини

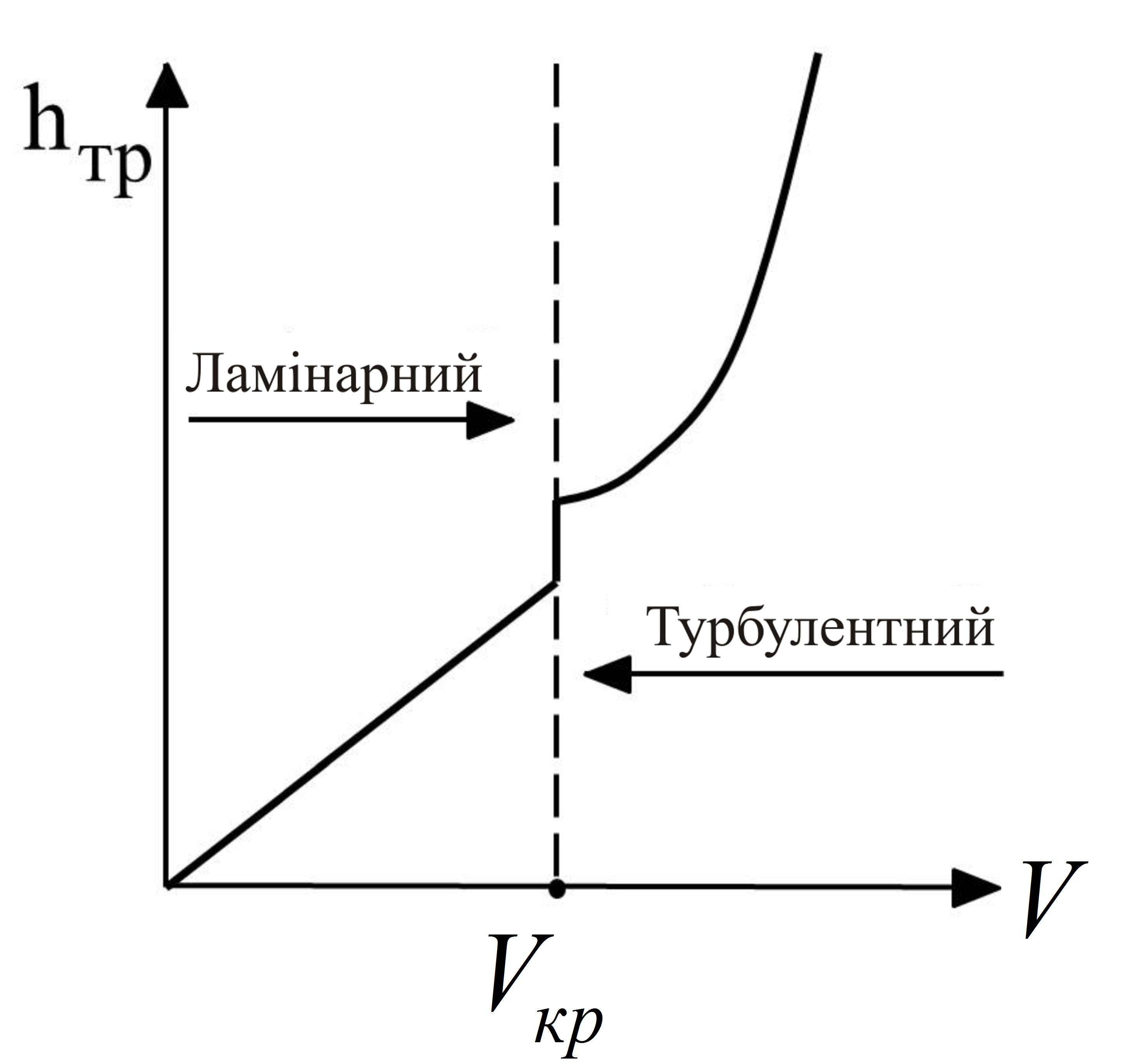ри ламінарному русі залежність втрат напору на тертя h_тр близька до лінійної (рис. 4.9). При турбулентному - втрати напору наростають більш інтенсивно і крива близька до параболи. Через складність турбулентного руху дотепер відсутня його строга теорія. У більшості випадків при розрахунках використовують експериментальні дані.

Основною розрахунковою формулою для визначення втрат напору при турбулентному русі є формула Дарсі-Вейсбаха:

(4.26)

де – гідравлічний коефіцієнт тертя при турбулентному режимі (коефіцієнт Дарсі).

При турбулентному режимі втрати напору пропорціональні квадрату швидкості. Коефіцієнт Дарсі _т залежить від діаметра труби d, числа Рейнольдса Re та шорсткості труби :

( 4.27)

При розрахунках використовують значення еквівалентної шорсткості труби _e.

Еквівалентна шорсткість _e – це уявна висота виступів на внутрішній поверхні труб, яка при обчисленні дає такі ж втрати напору, як і при наявності дійсних виступів.

3. Поняття про гідравлічно гладкі і шорсткі труби.

Схематично можна розглянути три області гідравлічних опорів: