3.4 Рівняння Бернуллі для ідеальної рідини
Розглянемо елементарну струминку ідеальної рідини, що знаходиться в усталеному русі.
Скористаємося диференціальними рівнянням руху рідини:
Помножимо перше
рівняння на
,
друге –
,
третє –
і
складемо :
(3.16)
Оскільки
;
;
,
(3.17)
то
;
;
.
(3.18)
Підставимо ці значення в ліву частину рівняння (3.16) і одержимо :
(3.19)
Враховуючи, що повна швидкість через її складові по вісям координат буде
,
(3.20)
можна записати :
.
(3.21)
У правій частині
рівняння (3.16) вираз
– є повним диференціалом деякої функції
,
частинні похідні якої дорівнюють :
.
(3.22)
Ця функція називається потенціальною або силовою.
З урахуванням (3.22) одержимо
.
(3.23)
Оскільки ми розглядаємо усталений рух, у якому тиск не залежить від часу , то тричлен у дужках являє собою повний диференціал тиску :
.
(3.24)
Отже остаточно рівняння (3.16) можна записати у вигляді :
,
(3.25)
або
.
(3.26)
Отримане
диференціальне рівняння встановлює
зв’язок між швидкістю
,
тиском
і силовою функцією
.
Проінтегруємо рівняння (3.26) :
.
(3.27)
Розглянемо елементарну струминку ідеальної рідини (рис.3.5) і виділемо два перерізи – 1-1 і 2-2.
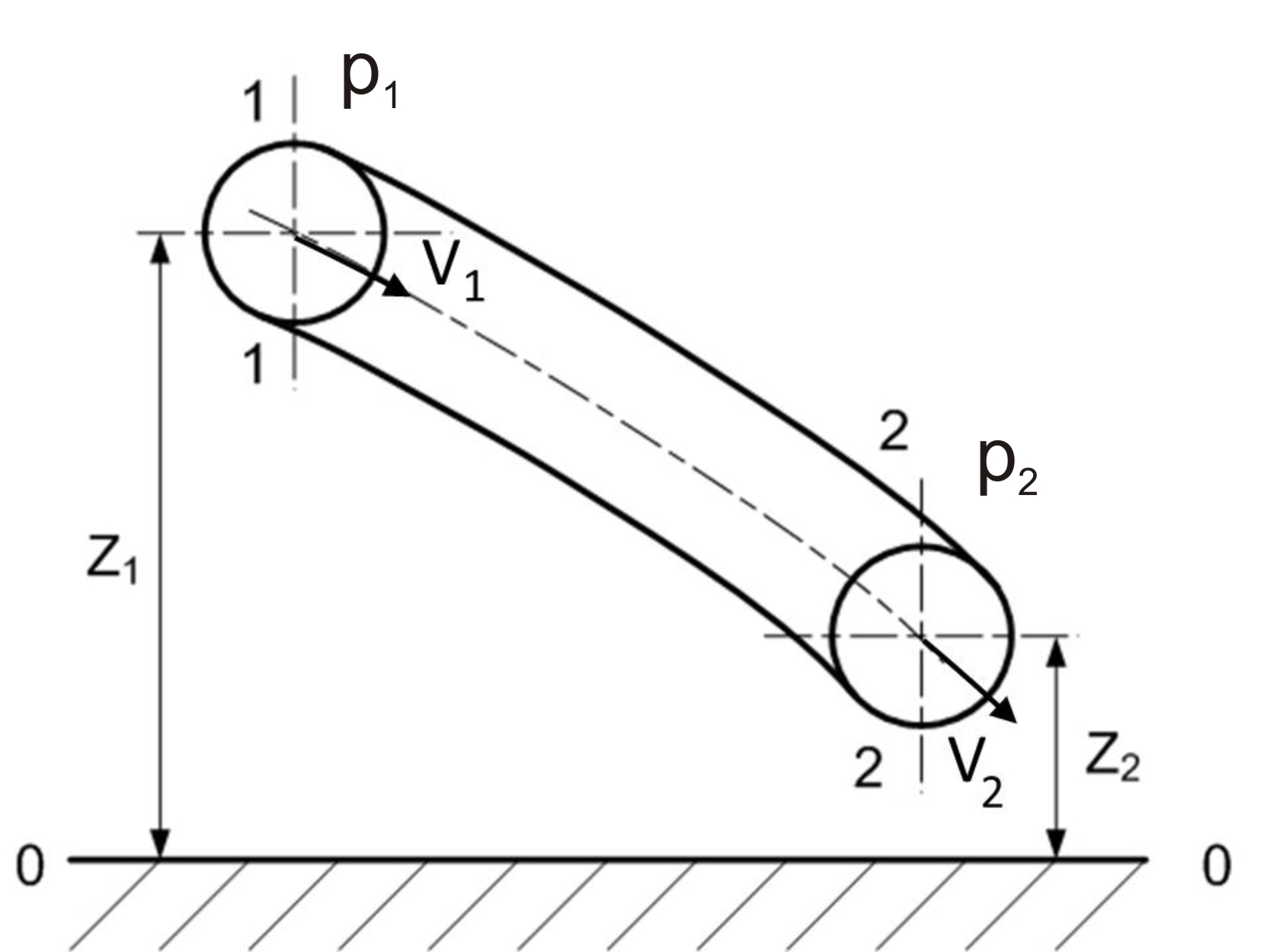
Рисунок 3.5 – Перерізи елементарної струминки
Ідеальної рідини
Для перерізів 1-1 та 2-2 можна записати :
.
(3.28)
Д
ля
часткового випадку,
коли на рідину діє тільки одна масова
сила - сила тяжіння,
Тоді функція З урахуванням цього
рівняння набирає вигляду
.
(3.29)
Розділимо всі
члени рівняння (3.29)
на
(віднесемо до одиниці ваги рідини) :
.
(3.30)
Це рівняння Бернуллі у формі напорів для елементарної струминки ідеальної рідини (всі члени рівняння вимірюються в метрах).
3.5 Геометричний і енергетичний зміст складових рівняння Бернуллі
Усім складовим рівняння Бернуллі можна дати пояснення з геометричної та енергетичної точки зору.
Візьмемо елементарну
струминку (рис. 3.6) і проведемо два
перерізи 1-1 та 2-2, розташованих на висотах
і
від площини порівняння 0-0.
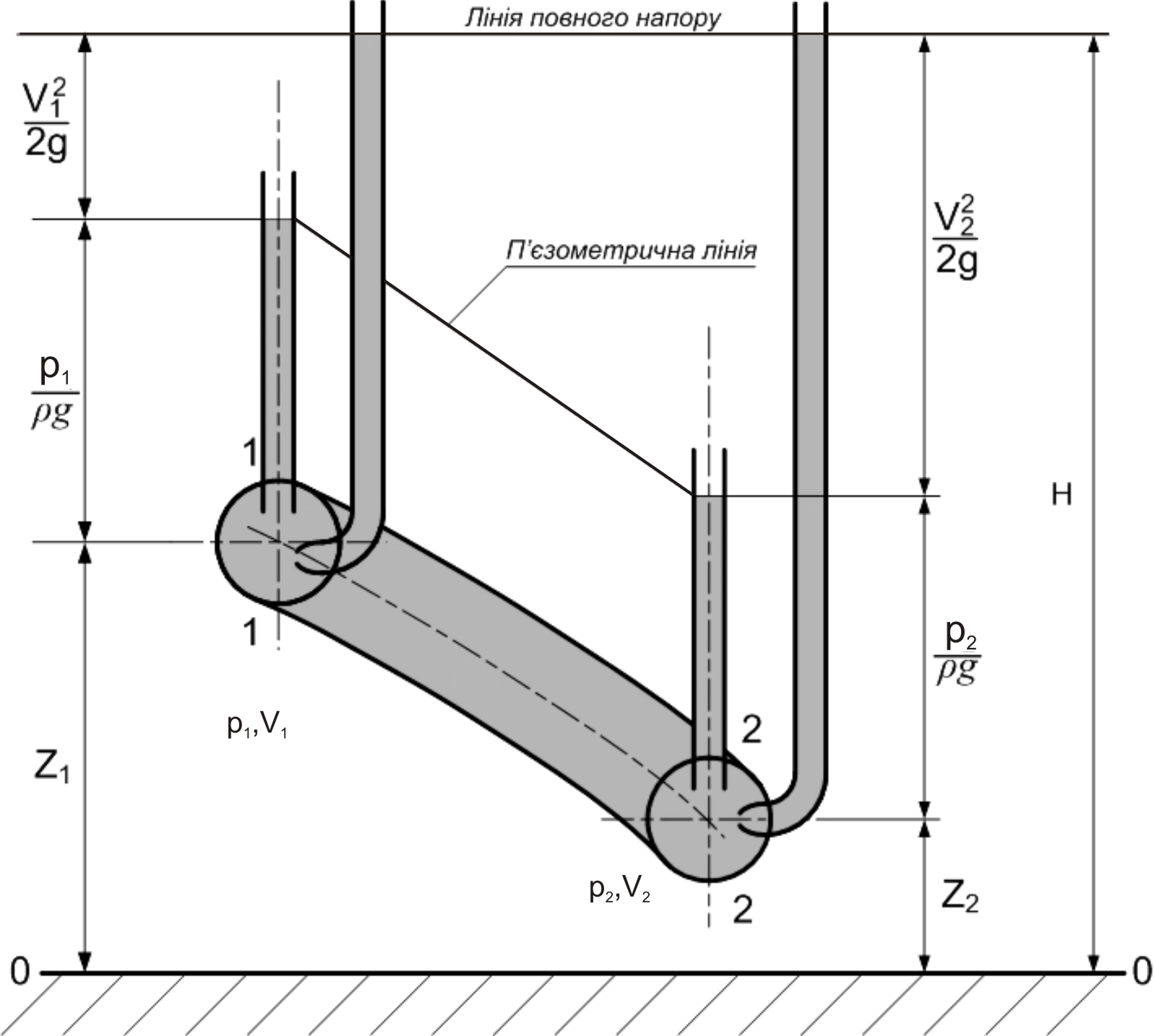
Рисунок 3.6 –
Зміна п’єзометричного і швидкісного
напорів вздовж струминки ідеальної
рідини
У
Рисунок 3.7 -
Прилади для вимірювання
швидкості в рідині
,
що називається п’єзометричною
висотою.
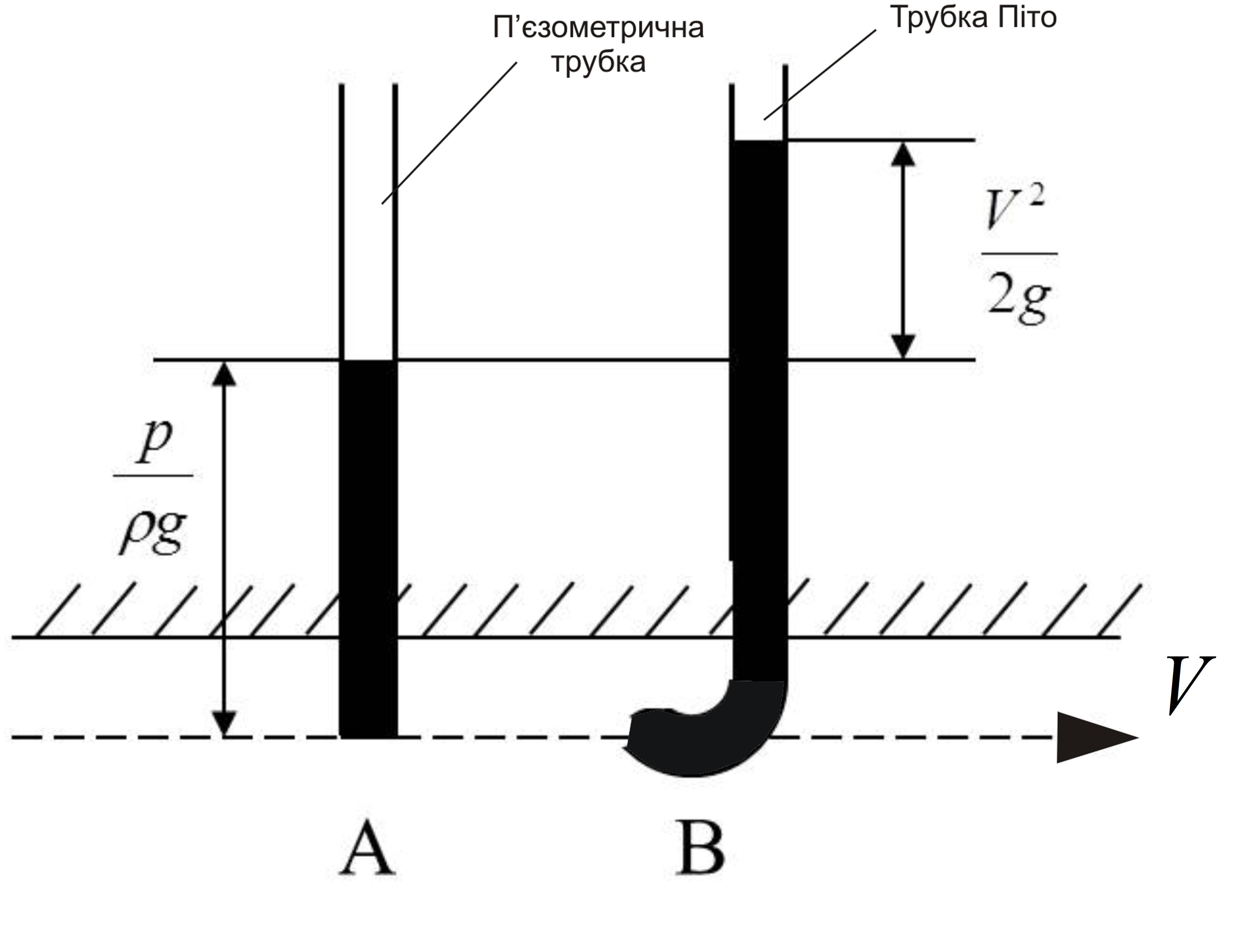
Попередньо розглянемо вимірювальний прилад, який називається трубкою Піто (рис. 3.7). Це вигнута під кутом 90° трубка з наконечником меншого діаметра, а ніж діаметр скляної трубки. Ця трубка служить для вимірювання швидкості в точці рідини, у якій вона поміщена.
У трубці Піто
рідина, у порівнянні з п’єзометричною
трубкою, додатково піднімається на
висоту
в звязку з тим, що частинки рідини, які
набігають на трубку зі швидкістю
,
створюють додатковий тиск на нерухому
рідину.
Запишемо рівняння Бернуллі для перерізів 1-1 і 2-2 :
,
(3.31)
де z- відстань від довільно вибраної горизонтальної площини до центра ваги кожного перерізу; р – тиск у центрі ваги перерізу; – середня швидкість рідини в цьому перерізі.
Розглянемо складові рівняння з геометричної точки зору.
1 Величина
– це
геометрична
висота або напір.
В гідравліці широко використовується
термін напір,
під яким
розуміють питому енергію.
2 Величину
називають п’єзометричною
висотою або напором .
3 Величина – це швидкісний (динамічний) напір.
Всю суму напорів називають повним напором Н.
Усі члени у цьому рівнянні Бернуллі мають лінійну розмірність.
Розглянемо енергетичний зміст рівняння Бернуллі.
З енергетичної
точки зору сума трьох складових
є повною питомою
енергією,
тобто енергією, віднесеною до одиниці
ваги рідини.
Окремі складові рівняння:
1) – питома потенціальна енергія (її величина залежить від положення центра ваги розглянутого перерізу над площею порівняння);
2) – питома потенціальна енергія тиску (її значення залежить від тиску );
3)
– питома потенціальна енергія;
4)
– питома кінетична енергія.
Рівнянню Бернуллі можна дати таке фізичне трактування:
Вздовж потоку рідини, в якій відсутні втрати енергії, повна питома енергія рідини залишається незмінною, тобто воно виражає закон збереження енергії елементарної струминки.