Задача третья.

Определение мини­мально необходимого диаметра трубо­провода для обеспечения заданного рас­хода Q при известном напоре в трубоп­роводе  . Эта задача может быть  решена, как и в предыдущем случае ана­литически, методом последовательных приближений или графоаналитически.

В последних двух случаях задаются рядом значений диаметров   и, зная Q, вычисляют потери напора  . В методе последовательных приближений срав­нивают получаемые значения потерь напора с заданными по условию задачи,

д обиваясь их близкого совпадения.

В графоаналитическом методе строится зависимость потерь напора от диаметра (рис. 6.4), а затем отложив по оси ординат предварительно вычисленные потери напора  на оси абсцисс нахо­дят минимально необходимый диаметр  . Если диаметр, определен­ный с этого графика, отсутствует в сортаменте, то берется ближайший большой диаметр.

            Рассмотрим случай последовательного соединения труб. Если трубопровод состоит из нескольких последовательно соединенных участков труб различного диаметра и различной длины (рис. 6.5), то задачи решаются изложенными способами. При этом полные потери напора на всем протяжении трубопровода определяются как сумма потерь на трение на отдельных участках и местных сопротивлений:

, а расход жидкости на каждом из участков одинаков 

Равенство (6.4) выражает собой принцип наложения потерь (принцип суперпозиции).

Принцип наложения может быть использован лишь в том случае, если расстояние между имеющимися местными сопротивлениями достаточно больше. Как показали опыты, если  , где L – расстояние между местными сопротивлениями, d – диаметр трубопровода, то взаимное влияние местных сопротивлений мало и в этом случае можно воспользоваться соотношением: 

Если требуется найти расход в последовательно соединенном трубопроводе при задаваемых значенияхнапора, то в качестве расчетного служит по-прежнему соотношение:  .

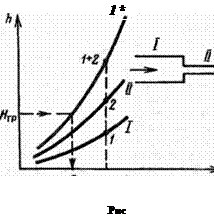
Если при этом заранее не известны коэффициенты λ и ζ, зависящие от расхода, то — так же как в случае простого трубопровода — эту задачу надо решать ме­тодом последовательных приближений или графоа­налитическим способом. С этой целью при нескольких значениях расхода, задавае­мых произвольно, строим гидравлическую характери­стику для каждого участка, и совмещаем графики на одном чертеже (строим совме­стную характеристику), как это показано на схеме (рис. 6.6) для тру­бопровода, состоящего из двух участков I и II; при этом для получе­ния точек совместной характеристики для каждого значения расхода Q суммируются соответствующие ему значения потерь напора h на каждом из участков. Таким образом, расстояние от оси абсцисс до са­мой верхней кривой равняется сумме потерь на всей длине трубопрово­да и поскольку располагаемая величина напора   известна — из графика можно определить соответствующий этому напору расход  .

20)Гидравлический расчёт простых длинных трубопроводов на основе использования обобщённых гидравлических параметров