31°. Направленный отрезок. Эквивалентные направленные отрезки. Понятие вектора. Угол между векторами. Коллинеарные и компланарные векторы.

Н аправленный отрезок - отрезок оси Δ ,ограниченный точками Α,Β, если указана, какая из этих точек является точкой начала, а какая точкой конца.

Направленные отрезки 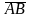и называются сонаправленными, (обозначается 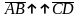), если они лежат на параллельных прямых и направлены в одну сторону.

Длиной направленного отрезка называется длина отрезка АВ.

Два направленных отрезка и считаются эквивалентными, если они сонаправлены и имеют равные длины.

Множество всех направленных отрезков, эквивалентных какому-нибудь одному, называется вектором.

Углом между ненулевыми векторами и называется угол ВАС. Углом между любыми двумя ненулевыми векторами и называется угол между изображающими их направленными отрезками с общим началом. Угол между одинаково направленными векторами считается равным нулю, противоположно направленными — .Угол между нулевым вектором и каким-либо другим не определён.

Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

Векторы называются компланарными, если существует плоскость, которой они параллельны.

Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.

32°. Операции над векторами. Свойства операции над векторами.

Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c - его диагональю

Сложение векторов в соответствии см. рисунком называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из следующего рисунка . Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.

Свойства сложения векторов.

1^о. .

2^о. .

3^о. , т.к. .

4^о. Для каждого вектора вектор, называемый вектором, противоположным , такой, что .

Если , то через обозначим . Тогда .

Произведением вектора на число называется вектор , удовлетворяющий следующим условиям:

векторы и сонаправлены, если и противоположно направлены, если ;

.

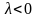Произведение вектора на число 0 есть нулевой вектор.

Пишут: .

Свойства умножения вектора на число.

и .

и вектора .

и вектора .

вектора .

В ычитание векторов. , т.е.

33. Понятие линейной зависимости векторов. Линейно независимые векторы. Необходимое и достаточное условие коллинеарности двух векторов. Необходимое и достаточное условие компланарности трех векторов.

Говорят, что векторы , , , линейно зависимы, если существуют числа , , , , не все равные нулю и такие, что линейная комбинация 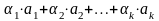равна нулевому элементу линейного пространства .

Если же равенство возможно только при условии , то векторы , , , называют линейно независимыми.

Лемма. Векторы , , , линейно зависимы тогда и только тогда, когда хотя бы один из них линейно выражается через оставшиеся.

Необходимое и достаточное условие коллинеарности двух ненулевых векторов

Теорема. Для того, чтобы два ненулевых вектора и были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было бы равно нулю.( a| | b  a,b - ЛЗВ )

Доказательство. Необходимость. Пусть векторы и коллинеарны, тогда они лежат на одной прямой, следовательно, => . Значит,

Достаточность. Пусть векторное произведение . Так как 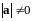, , то значит , т.е. или , а это означает, что векторы и b коллинеарны.

Необходимое и достаточное условие компланарности трёх векторов

Теорема. Для того чтобы ненулевые векторы a,b и c были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.(a₁, a₂, a₃ – комплонарны  a₁, a₂, a₃ - ЛЗВ)

Доказательство. Необходимость. Пусть векторы a,b,c компланарны. Тогда их можно поместить в одной плоскости, и вектор окажется перпендикулярным векторy a, следовательно, их скалярное произведение равно нулю, т.е. .

Достаточность. Пусть . Так как векторы ненулевые, то может быть:

1) , тогда , следовательно, векторы a,b,c можно поместить в одной плоскости, т.е. они компланарны;

2) 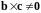, но => . Это значит, что вектор a лежит в одной плоскости с векторами b и c.