Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид  φ = φ₀ + ωt.

В частном случае, когда начальный угол поворота φ₀=0,  φ = ωt.

Угловую скорость равномерно вращающегося тела  ω = φ/t  можно выразить и так:  ω = 2π/T,  где T – период вращения тела; φ=2π – угол поворота за один период.

Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным. .Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным. Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения  (1)φ = φ₀ + ω₀t + εt²/2  и уравнение, выражающее угловую скорость тела в любой момент времени,  (2)ω = ω₀ + εt  представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ₀, ω₀ и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:  (3)φ = φ₀ + (ω + ω₀)t/2.

Исключим из (1) и (2) время t:  (4)φ = φ₀ + (ω² - ω₀²)/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ₀=0 и ω₀=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:  (5)φ = εt²/2;  (6)ω = εt;  (7)φ = ωt/2;  (8)φ = ω²/(2ε).

Центр масс

Центр масс, центр инерции, барицентр — геометрическая точка, характеризующая движение тела или системы частиц как целого. Не является тождественным понятию центра тяжести (хотя чаще всего совпадает).

Определение

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

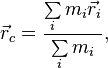
где   — радиус-вектор центра масс,   — радиус-вектор i-й точки системы,   — масса i-й точки.

Для случая непрерывного распределения масс:

где   — суммарная масса системы,   — объём,   — плотность. Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

Можно показать, что если система состоит не из материальных точек, а из протяжённых тел с массами  , то радиус-вектор центра масс такой системы   связан с радиус-векторами центров масс тел   соотношением:

Иначе говоря, в случае протяжённых тел справедлива формула, по своей структуре совпадающая с той, что используется для материальных точек.

Теорема о движении центра масс системы — одна из общих теорем динамики, является следствием законов Ньютона. Утверждает, что ускорение центра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему.

Объектами, о которых идёт речь в теореме, могут, в частности, являться следующие:

• система материальных точек

• протяжённое тело или система протяжённых тел

• вообще любая механическая система, состоящая из любых тел