
- •Примеры
- •Вывод из уравнений Ньютона
- •Физический смысл
- •Физический смысл работы
- •Определение
- •Работа силы (сил) над одной точкой
- •Работа силы (сил) над системой или неточечным телом
- •Кинетическая энергия
- •Потенциальная энергия
- •Консервативные силы
- •Диссипативные силы
- •Особенности
- •Пример диссипативных сил
- •Равномерное вращательное движение
- •Равнопеременное вращательное движение
- •Центр масс
- •Определение
- •Формулировка теоремы
- •Доказательство
- •Момент силы
- •Общие сведения
- •Единицы
- •Специальные случаи Формула момента рычага
- •Момент импульса в классической механике Определение
- •Вычисление момента
- •Сохранение углового момента
- •Момент инерции
- •Осевой момент инерции
- •Теорема Гюйгенса — Штейнера
- •Осевые моменты инерции некоторых тел
- •Энергия вращательного движения
- •Принцип относительности Галилея
- •Вид преобразований при коллинеарных осях
- •Релятивистская механика
- •Строгое определение
- •Релятивистское замедление времени
- •Второй закон Ньютона в релятивистской механике
- •Формулировки
- •Напряжённость электрического поля
- •Электростатический потенциал
- •Неоднозначность определения потенциала
- •Кулоновский потенциал
- •Применение теоремы Гаусса
- •Электрическое поле диполя
- •Действие поля на диполь
- •Зависимость вектора поляризации от внешнего поля в постоянном поле
- •Физическая природа
- •Теорема Гаусса для электрической индукции (электрического смещения)
- •Диэлектрическая восприимчивость
- •Диэлектрическая проницаемость
- •Некоторые свойства
- •Электрический конденсатор
- •Свойства конденсатора
- •Основные параметры Ёмкость
- •Удельная ёмкость
- •Энергия электрического поля (не для конденсатора)(общая)
- •Закон Ома
- •Мнемоническая диаграмма для Закона
- •Закон Ома в дифференциальной форме
- •Закон Джоуля — Ленца
- •Определения
- •Электрическая мощность Электрическая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Мгновенная электрическая мощность
- •Закон Ампера
- •Сила Лоренца
- •Уравнение (единицы си)
- •Закон Био — Савара — Лапласа
- •Для тока, текущего по контуру (тонкому проводнику)
- •Теорема о циркуляции магнитного поля
- •Математическая формулировка
- •Магнитный момент
- •Формулы для вычисления магнитного момента
- •Напряжённость магнитного поля
- •Намагниченность
- •Магнитная восприимчивость
- •Определение
- •Свойства ферромагнетиков
- •Магнитный поток
- •Закон Фарадея
- •Вихревое электрическое поле
- •Энергия магнитного поля
- •§1.3. Второе уравнение Максвелла.
- •§1.4. Третье уравнение Максвелла. Закон сохранения заряда.
- •§1.5. Четвертое уравнение Максвелла.
- •Характеристики
- •Гармонические колебания
- •Виды колебаний
- •Определения
- •Энергия гармонических колебаний
- •2.2. Затухающие электромагнитные колебания
- •Логарифмический декремент колебаний
- •Вынужденные колебания
- •Вынужденные колебания гармонического осциллятора
- •Волновое уравнение
- •Вид уравнения
- •Определение
- •Гармоническая волна
- •Одномерный случай
- •Случаи пространства размерностью больше единицы
- •Гармоническая волна
- •Дисперсия
- •Энергия упругой плоской волны
- •Поляризация волн
- •Поляризация электромагнитных волн
- •Теория явления[
- •Поляризация монохроматических волн
Поляризация монохроматических волн
В
случае плоской монохроматической
волны компоненты вектора
напряженности
электрического поля (также
как и компоненты вектора ![]() напряженности
магнитного поля) меняются совместно
по гармоническому
закону:
напряженности
магнитного поля) меняются совместно
по гармоническому
закону:
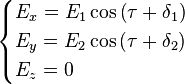
Здесь
набег фазы ![]() .
.
Преобразовав и сложив первые два уравнения, можно получить уравнение движения вектора :
![]() ,
где разность фаз
,
где разность фаз ![]() .
.
Эта квадратичная
форма описывает эллипс.
То есть конец вектора напряженности
плоской монохроматической волны
описывает эллипс. Для того, чтобы привести
её к каноническому виду, нужно повернуть
эллипс на угол ![]() :
:

Любой эллипс можно задать в параметрической форме:

Здесь ![]() и
и ![]() —
амплитудные значения компонент вектора
,
соответствующие большой и малой полуосям
эллипса. Из последних двух систем
уравнений можно сделать следующий
вывод:
—
амплитудные значения компонент вектора
,
соответствующие большой и малой полуосям
эллипса. Из последних двух систем
уравнений можно сделать следующий
вывод:
![]() ,
,
где ![]() — вектор
Пойнтинга. Таким образом, в плоской
монохроматической волне величина
вектора Пойнтинга равна сумме потоков
в двух произвольных ортогональных
направлениях. Вводя обозначения
— вектор
Пойнтинга. Таким образом, в плоской
монохроматической волне величина
вектора Пойнтинга равна сумме потоков
в двух произвольных ортогональных
направлениях. Вводя обозначения ![]() и
и ![]() ,
из тех же двух систем уравнений можно
вывести соотношения:
,
из тех же двух систем уравнений можно
вывести соотношения:
![]()
и
![]() .[4]
.[4]
С
помощью последних трех уравнений можно
вычислить все параметры эллиптически
поляризованной волны. А именно, зная
величины ![]() и
и ![]() в
произвольной системе координат, можно
вычислить величину вектора Пойнтинга.
С помощью разности фаз
в
произвольной системе координат, можно
вычислить величину вектора Пойнтинга.
С помощью разности фаз ![]() можно
определить угол поворота большой оси
эллипса
относительно
нашей системы координат, а также величины
большой и малой полуосей эллипса
и
.
можно
определить угол поворота большой оси
эллипса
относительно
нашей системы координат, а также величины
большой и малой полуосей эллипса
и
.
Направление
вращения волнового
вектора определяется
разностью фаз
.
Если ![]() ,
тогда поляризация называется правой,
а если, напротив,
,
тогда поляризация называется правой,
а если, напротив, ![]() ,
поляризация называется левой. Если
наблюдатель смотрит навстречу световому
лучу, то правой поляризации соответствует
движение конца вектора по часовой
стрелке, а левой поляризации — против
часовой стрелки. Если разность фаз
равна
,
поляризация называется левой. Если
наблюдатель смотрит навстречу световому
лучу, то правой поляризации соответствует
движение конца вектора по часовой
стрелке, а левой поляризации — против
часовой стрелки. Если разность фаз
равна ![]() ,
где
—
целое число, то эллипс вырождается в
отрезок. Такая поляризация называется
линейной. Другой важный случай возникает,
когда
,
где
—
целое число, то эллипс вырождается в
отрезок. Такая поляризация называется
линейной. Другой важный случай возникает,
когда ![]() и
и ![]() .
В этом случае эллипс превращается в
окружность, параметрическое уравнение
которой имеет вид:
.
В этом случае эллипс превращается в
окружность, параметрическое уравнение
которой имеет вид:

Нетрудно убедиться, что произвольная эллиптическая поляризация может быть разложена на сумму правой и левой круговых поляризаций.
Параметры Стокса
Для описания поляризации плоской монохроматической волны достаточно трёх параметров, например полудлин сторон прямоугольника, в который вписан эллипс поляризации , и разностью фаз , либо полуосей эллипса , и углa между осью и большой осью эллипса. Стоксом было предложено альтернативное описание поляризации с помощью четырёх параметров, получивших его имя.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Независимыми являются только три из них, ибо справедливо тождество:
![]() .
.
Используя
вспомогательный угол
,
определяемый выражением ![]() (знак
(знак ![]() соответствует
левой, а
соответствует
левой, а ![]() —
правой поляризации[5]),
то можно получить следующие выражения
для параметров Стокса:
—
правой поляризации[5]),
то можно получить следующие выражения
для параметров Стокса:
![]() ,
,
![]() ,
,
![]() .
.
На основе этих формул можно
характеризовать поляризацию световой
волны наглядным геометрическим способом.
При этом параметры Стокса ![]() ,
, ![]() ,
, ![]() интерпретируются,
как декартовы координаты точки, лежащей
на поверхности сферы радиуса
интерпретируются,
как декартовы координаты точки, лежащей
на поверхности сферы радиуса ![]() .
Углы
.
Углы ![]() и
и ![]() имеют
смысл сферических угловых координат
этой точки. Такое геометрическое
представление предложил Пуанкаре,
поэтому эта сфера называется сферой
Пуанкаре. В
математике этой модели соответствует сфера
Римана, в других
разделах физики — сфера
Блоха.
имеют
смысл сферических угловых координат
этой точки. Такое геометрическое
представление предложил Пуанкаре,
поэтому эта сфера называется сферой
Пуанкаре. В
математике этой модели соответствует сфера
Римана, в других
разделах физики — сфера
Блоха.
Наряду
с
,
,
используют
также нормированные параметры
Стокса ![]() ,
, ![]() ,
, ![]() .
Для поляризованного света
.
Для поляризованного света ![]() .
.
s- и p-поляризации волн
Подробнее смотрите Формулы Френеля.
В оптике и электродинамике s-поляризованная волна (сравните нем. senkrecht - перпендикулярный) имеет вектор электрического поля E, перпендикулярный плоскости падения. s-поляризованную волну также называют σ-поляризованной, сагиттально поляризованной, волной E-типа, TE-волной]. p-поляризованная волна (сравните лат. parallel - параллельный) имеет вектор электрического поля E, параллельный плоскости падения. p-поляризованную волну также называют π-поляризованной, поляризованной в плоскости падения, волной H-типа, TM-волной (Transverse Magnetic).
Термины TM-волна и TE-волна в работах ряда авторов меняются местами. Дело в том, что классически плоская граница предполагает однородность структуры в двух направлениях. В этом случае определяют плоскость падения и перпендикулярность напряженностей по отношению к ней. Разделение электромагнитного поля на два несвязанных решения возможно в более общем случае структуры, однородной в одном направлении. В этом случае удобно определять перпендикулярность напряженностей по отношению к направлению однородности. Распространение последнего определения на частный классический случай приводит к тому, что напряженность, перпендикулярная к направлению однородности, оказывается в плоскости падения. Отмечается, что в случае металлической поверхности существенны только волны с электрической напряженностью, перпендикулярной к границе металла. Такие волны также удобнее называть TE-волнами. Термины TM и TE связаны также с обозначением поперечных мод в лазерном резонаторе или волноводе.
В сейсмологии p-волна (от англ. primary - первичный) - продольная волна, приходящая от эпицентра землетрясения первой. s-волна (от англ. secondary - вторичный) - поперечная волна (shear wave), имеющая меньшую скорость распространения, чем продольная, и поэтому приходящая от эпицентра позднее.
