
- •Примеры
- •Вывод из уравнений Ньютона
- •Физический смысл
- •Физический смысл работы
- •Определение
- •Работа силы (сил) над одной точкой
- •Работа силы (сил) над системой или неточечным телом
- •Кинетическая энергия
- •Потенциальная энергия
- •Консервативные силы
- •Диссипативные силы
- •Особенности
- •Пример диссипативных сил
- •Равномерное вращательное движение
- •Равнопеременное вращательное движение
- •Центр масс
- •Определение
- •Формулировка теоремы
- •Доказательство
- •Момент силы
- •Общие сведения
- •Единицы
- •Специальные случаи Формула момента рычага
- •Момент импульса в классической механике Определение
- •Вычисление момента
- •Сохранение углового момента
- •Момент инерции
- •Осевой момент инерции
- •Теорема Гюйгенса — Штейнера
- •Осевые моменты инерции некоторых тел
- •Энергия вращательного движения
- •Принцип относительности Галилея
- •Вид преобразований при коллинеарных осях
- •Релятивистская механика
- •Строгое определение
- •Релятивистское замедление времени
- •Второй закон Ньютона в релятивистской механике
- •Формулировки
- •Напряжённость электрического поля
- •Электростатический потенциал
- •Неоднозначность определения потенциала
- •Кулоновский потенциал
- •Применение теоремы Гаусса
- •Электрическое поле диполя
- •Действие поля на диполь
- •Зависимость вектора поляризации от внешнего поля в постоянном поле
- •Физическая природа
- •Теорема Гаусса для электрической индукции (электрического смещения)
- •Диэлектрическая восприимчивость
- •Диэлектрическая проницаемость
- •Некоторые свойства
- •Электрический конденсатор
- •Свойства конденсатора
- •Основные параметры Ёмкость
- •Удельная ёмкость
- •Энергия электрического поля (не для конденсатора)(общая)
- •Закон Ома
- •Мнемоническая диаграмма для Закона
- •Закон Ома в дифференциальной форме
- •Закон Джоуля — Ленца
- •Определения
- •Электрическая мощность Электрическая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Мгновенная электрическая мощность
- •Закон Ампера
- •Сила Лоренца
- •Уравнение (единицы си)
- •Закон Био — Савара — Лапласа
- •Для тока, текущего по контуру (тонкому проводнику)
- •Теорема о циркуляции магнитного поля
- •Математическая формулировка
- •Магнитный момент
- •Формулы для вычисления магнитного момента
- •Напряжённость магнитного поля
- •Намагниченность
- •Магнитная восприимчивость
- •Определение
- •Свойства ферромагнетиков
- •Магнитный поток
- •Закон Фарадея
- •Вихревое электрическое поле
- •Энергия магнитного поля
- •§1.3. Второе уравнение Максвелла.
- •§1.4. Третье уравнение Максвелла. Закон сохранения заряда.
- •§1.5. Четвертое уравнение Максвелла.
- •Характеристики
- •Гармонические колебания
- •Виды колебаний
- •Определения
- •Энергия гармонических колебаний
- •2.2. Затухающие электромагнитные колебания
- •Логарифмический декремент колебаний
- •Вынужденные колебания
- •Вынужденные колебания гармонического осциллятора
- •Волновое уравнение
- •Вид уравнения
- •Определение
- •Гармоническая волна
- •Одномерный случай
- •Случаи пространства размерностью больше единицы
- •Гармоническая волна
- •Дисперсия
- •Энергия упругой плоской волны
- •Поляризация волн
- •Поляризация электромагнитных волн
- •Теория явления[
- •Поляризация монохроматических волн
Энергия упругой плоской волны
Пусть
дано, что ![]()
Выделим
в пространстве некий малый объём ![]() ,
настолько малый, что во всех точках
этого объёма скорость движения частиц
,
настолько малый, что во всех точках
этого объёма скорость движения частиц ![]() и
деформацию
и
деформацию ![]() можно
считать постоянными.
можно
считать постоянными.
Тогда данный объёмчик обладает кинетической энергией
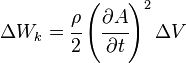
и потенциальной энергией упругой деформации

Полная энергия это
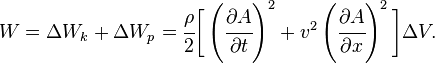
Плотность энергии, соответственно, равна

Поляризация волн
Поляризация волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.
В продольной волне поляризация возникнуть не может, так как направление колебаний в этом типе волн всегда совпадают с направлением распространения.
Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Волновой вектор показывает направление распространения волны, а вектор поляризации представляет собой вектор напряженности электрического поля. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.
Причиной возникновения поляризации волн может быть:
несимметричная генерация волн в источнике возмущения;
анизотропность среды распространения волн;
преломление и отражение на границе двух сред.
В общем случае для гармонических волн конец вектора колеблющейся величины описывает в плоскости, поперечной направлению распространения волны, эллипс, и такая поляризация называется эллиптической. Важными частными случаями являются линейная поляризация, при которой колебания возмущения происходят в какой-то одной плоскости, в таком случае говорят о «плоско-поляризованной волне», и круговая или циркулярная поляризация, при которой конец вектора амплитуды описывает окружность в плоскости колебаний, круговая поляризация в зависимости от направления вращения вектора может быть правой или левой.
Поляризация описывается Фигурами Лиссажу и соответствует сложению поперечных колебаний равной частоты.
Поляризация электромагнитных волн
Для электромагнитных волн поляризация — явление направленного колебания векторов напряженности электрического поля E или напряженности магнитного поля H.
Теория явления[
Электромагнитная волна может быть разложена (как теоретически, так и практически) на две поляризованные составляющие, например, поляризованные вертикально и горизонтально. Возможны другие разложения, например, по иной паре взаимно перпендикулярных направлений, или же на две составляющие, имеющие левую и правую круговую поляризацию. При попытке разложить линейно поляризованную волну по круговым поляризациям (или наоборот) возникнут две составляющие половинной интенсивности.
Как с квантовой, так и с классической точки зрения, поляризация может быть описана двумерным комплексным вектором (вектором Джонса). Поляризация фотона является одной из реализаций q-бита.
Свет солнца, являющийся тепловым излучением, не имеет поляризации, однако рассеянный свет неба приобретает частичную линейную поляризацию. Поляризация света меняется также при отражении. На этих фактах основаны применения поляризующих фильтров в фотографии и т. д.
Линейную поляризацию имеет обычно излучение антенн.
По изменению поляризации света при отражении от поверхности можно судить о структуре поверхности, оптических постоянных, толщине образца.
Если рассеянный свет поляризовать, то, используя поляризационный фильтр с иной поляризацией, можно ограничивать прохождение света. Интенсивность света, прошедшего через поляризаторы, подчиняется закону Малюса. На этом принципе работают жидкокристаллические экраны.
Некоторые живые существа, например пчёлы, способны различать линейную поляризацию света, что даёт им дополнительные возможности для ориентации в пространстве. Обнаружено, что некоторые животные, например креветка-богомол павлиновая способны различать циркулярно-поляризованный свет, то есть свет с круговой поляризацией.
