Вид уравнения

В многомерном случае однородное волновое уравнение записывается в виде

,

где   — оператор Лапласа,   — неизвестная функция,   — время,   — пространственная переменная,   — фазовая скорость.

В одномерном случае уравнение называется также уравнением колебания струны или уравнением продольных колебаний стержня и записывается в виде

.

Плоская волна — волна постоянной частоты, волновые фронты которой являются бесконечными плоскостями, нормальными к вектору фазовой скорости.

Такие волны в реальности не существуют, так как плоская волна начинается в точке   и заканчивается в точке  , чего, очевидно, быть не может. Тем не менее, конечная плоская волна существует и называется «квазиплоской». Если квазиплоская волна обладает достаточной длиной, то её приближённо можно считать плоской (под длиной здесь подразумевается протяжённость волны, длина же волны   здесь будет называться «пространственным периодом колебаний»).

Определение

Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Волновое уравнение для функции   записывается в виде

где

•  — оператор Лапласа;

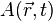•  — искомая функция;

•  — радиус-вектор искомой точки;

•  — скорость волны;

 — время.

Одномерный случай

Плоская гармоническая волна задаётся уравнением

где

 — величина возмущения в данной точке пространства   и времени  ;

 — амплитуда волны;

 — волновое число;

 — круговая частота;

 — начальная фаза колебаний.

Волну можно описать одним из уравнений

где

 — пространственный период колебаний;

 — период колебаний.

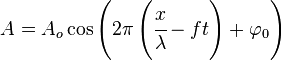
где

 — частота колебаний.

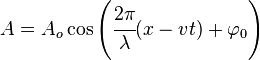
где

 — скорость движения волны.

Многомерный случай

В общем случае уравнения плоской волны записывается в виде

где

 — волновой вектор, равный 

где

 — волновое число;

 — единичный вектор нормали, проведённый к волновому фронту

 — радиус-вектор точки;

 — скалярное произведение векторов   и  . Здесь и далее скалярное произведение будет обозначаться таким образом.

Гармоническая волна

Гармоническая волна — согласно наиболее общему определению — волна, каждая точка колеблющейся среды или поле в каждой точке пространства совершает гармонические колебания. В разных случаях при необходимости особо выделяется интересующий класс гармонических волн, например, плоская гармоническая волна, стоячая гармоническая волна и т. д. (см. ниже).

Слово 'гармоническая' тут является синонимом слова 'монохроматическая', однако, по-видимому, не совсем точным; во всяком случае, обычные области применения того и другого термина обычно несколько различаются.

Источниками гармонических волн могут быть гармонические колебания, они также могут возбуждаться в какой-либо системе при взаимодействии ее с гармонической волной.

Одномерный случай

Случай одномерного однородного пространства (или одномерной однородной среды) — наиболее прост.

В этом случае все виды гармонических волн сводятся к:

• синусоидальным (косинусоидальным) бегущим волнам:

• или бегущим волнам виде мнимой экспоненты:

а также к конечным линейным комбинациям волн такого вида (для выражения произвольной действительной гармонической волн в этом случае достаточно смешать две волны первого вида или четыре второго; в случае более многомерного u добавляется по два таких слагаемых на каждую поляризацию).

• Может быть также использовано понятие гармонической стоячей волны, сводящейся к сумме двух гармонических бегущих (бегущих в противоположных направлениях) волн, описанных выше:

Здесь A — постоянный (не зависящий от x и t) коэффициент, природа и размерность которого свпадает с природой и размерностью поля u; k, ω и φ₀ — также постоянные параметры, в рассматриваемом одномерном случае все они — действительные числа (в отличие от более многомерных, где k становится векторным — для плоских волн). A — есть амплитуда волны, k — волновое число, ω — (циклическая) частота и φ₀ — начальная фаза — то есть фаза волны при x = t = 0.

Во второй формуле A — (обычно) комплексное, амплитуду волны определяет его модуль |A|, а начальная фаза спрятана также в A в качестве его аргумента, поскольку

Так же, как стоячая волна выражается (как записано здесь) через две бегущих, так же и бегущая может быть выражена через две стоячих. Поэтому можно выбрать один из двух равноправных способов выражения произвольной гармонической волны в случае одномерного однородного пространства: через линейную комбинацию бегущих или линейную комбинацию стоячих волн. Это верно и для всех других случаев, хотя базисные волны, через линейную комбинацию которых выражается произвольная гармоническая волна, могут оказаться сложнее.

• случай неоднородного одномерного пространства (неоднородной среды) оказывается значительно сложнее. В этом случае зависимость гармонических волн от пространственной координаты x становится не синусоидальной, а в общем — и наиболее типичном — случае и вовсе не выражается через элементарные функции. Тем не менее, и в этом случае остается верным утверждение о возможности выразить произвольную гамоническую волну через конечное (для определенной частоты) количество базисных гармонических волн.