§1.4. Третье уравнение Максвелла. Закон сохранения заряда.

 

Третье уравнение Максвелла определяет источники электрического поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.

Исходным для этого уравнения является уравнение Гаусса, которое говорит о том, что поток вектора   через замкнутую поверхность S равен заряду Q, заключенному в данной поверхности:

где ρ – объемная плотность заряда.

Подставим 1.24 в 1.23, получим

Уравнение 1.25 есть третье уравнение Максвелла в интегральной форме.

Для того чтобы получить интегральную форму, воспользуемся теоремой Гаусса-Остроградского, которая устанавливает связь между объемным и поверхностным интегралом:

Применим 1.26 к левой части уравнения  1.25, получим

Данное равенство справедливо только в том случае, когда равны подынтегральные функции:

Уравнение 1.27 – третье уравнение Максвелла в интегральной форме.

Заменим

и получим следующее уравнение

Для переменных полей заряды и токи связаны соотношением

 

где         - сила тока проводимости;

            j_пр – плотность тока проводимости;

 

В итоге, с учетом этих соотношений получим

 

Воспользуемся теоремой Гаусса – Остроградского

Или

Уравнение 1.30 выражает закон сохранения заряда:

            Источник тока проводимости – это изменение заряда во времени.

Уравнение 1.30 также является необходимым дополнением к системе уравнений Максвелла, так как в этой системе необходимо было связать ρ и  . Это уравнение можно вывести, воспользовавшись уже имеющимися уравнениями Максвелла. Запишем систему уравнений Максвелла

Применим оператор div к первому уравнению Максвелла:

 

§1.5. Четвертое уравнение Максвелла.

 

Четвертое уравнение Максвелла устанавливает отсутствие магнитных зарядов и то, что магнитные силовые линии всегда замкнуты. В интегральном виде этот факт записывается в виде уравнения

Поток вектора магнитной индукции через замкнутую поверхность равен нулю, поскольку магнитных зарядов одного знака в природе не обнаружено.

Применяя теорему Гаусса – Остроградского

Или

Уравнение 1.31 – это четвертое уравнение Максвелла в дифференциальной форме.

Колебания и волны.

Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.

Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.

Характеристики

• Амплитуда— максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы,   (м)

• Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание),   (с)

• Частота — число колебаний в единицу времени, 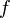  (Гц, с⁻¹).

Период колебаний   и частота   — обратные величины;

 и 

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота   (рад/с, Гц, с⁻¹), показывающая число колебаний за   единиц времени:

• Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения — метр.

• Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.