Мнемоническая диаграмма для Закона

В соответствии с этой диаграммой формально может быть записано выражение:

 (7)

Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

 (8)

где:

•  — удельное сопротивление материала, из которого сделан проводник,

•  — его длина

•  — площадь его поперечного сечения

Закон Ома в дифференциальной форме

Сопротивление   зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

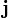•  — вектор плотности тока,

•  — удельная проводимость,

•  — вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость   является симметричным тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред.

Закон Джоуля — Ленца

Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем.

Определения

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля

Математически может быть выражен в следующей форме:

где   — мощность выделения тепла в единице объёма,   — плотность электрического тока,   — напряжённость электрического поля, σ — проводимость среды.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка

В математической форме этот закон имеет вид

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ до t₂. В случае постоянных силы тока и сопротивления:

Электрическая мощность Электрическая мощность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Мгновенная электрическая мощность

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки   в точку  , к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки   в точку  . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения:

 — напряжение на участке   (принимаем его постоянным на интервале  ,

 — количество зарядов, прошедших от   к   за время  ,

 — работа, совершённая зарядом   при движении по участку  ,

 — мощность.

Записывая вышеприведённые рассуждения, получаем:

Для единичного заряда на участке  :

Для всех зарядов:

Поскольку ток есть количество зарядов в единицу времени, то есть   по определению, в результате получаем:

.

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

мгновенная электрическая мощность  , выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения   и силы тока   на этом участке:

Если участок цепи содержит резистор c электрическим сопротивлением  , то

.

Дифференциальные выражения для электрической мощности

Мощность, выделяемая в единице объёма, равна:  ,

где   — напряжённость электрического поля,   — плотность тока. Отрицательное значение скалярного произведения означает, что в данной точке электрическая мощность не рассеивается, а генерируется за счёт работы сторонних сил.

В случае изотропной среды в линейном приближении:  ,

где   — удельная проводимость, величина, обратная удельному сопротивлению.

В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:  ,

где   — тензор проводимости.

Мощность постоянного тока

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:

.

Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:

, где   — электрическое сопротивление.

Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:

, где   — ЭДС.

Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность   прибавляется к поглощаемой или вычитается из отдаваемой.

Магнитное поле в вакууме.

Магнитное поле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля.

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции   (вектор индукции магнитного поля). С математической точки зрения   — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

• Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции  а вектор напряжённости магнитного поля  , что формально можно сделать, так как в вакууме эти два вектора совпадают; однако в магнитной среде вектор   не несет уже того же физического смысла, являясь важной, но всё же вспомогательной величиной. Поэтому при формальной эквивалентности обоих подходов для вакуума, с систематической точки зрения следует считать основной характеристикой магнитного поля именно