Кинематика.

Кинематика точки

Кинематика точки  — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Движение любого объекта в кинематике изучают по отношению к некоторой системе отсчета, включающей:

• Тело отсчета;

• Систему измерения положения тела в пространстве (систему координат);

• Прибор для измерения времени (Часы).

Положение точки определяется набором обобщенных координат — упорядоченным набором числовых величин, полностью описывающих положение тела. В самом простом случае это координаты точки (радиус-вектора) в выбранной системе координат. Наиболее наглядное представление о радиус-векторе можно получить в евклидовой системе координат, поскольку базис в ней является фиксированным и

Основные кинематические понятия

Материальная точка  — тело, размерами которого по сравнению с характерными расстояниями данной задачи можно пренебречь. Так Землю можно считать Материальной Точкой (М. Т.) при изучении её движения вокруг Солнца, пулю можно считать М. Т. при её движении в поле тяжести Земли, но нельзя считать таковой при учете её вращательного движения в стволе винтовки. При поступательном движении в ряде случаев при помощи понятия М. Т. можно описывать и изменение положения более крупных объектов. Так, например, тепловоз, проходящий расстояние 1 метр, может считаться М. Т., поскольку его ориентация относительно системы координат в процессе движения является фиксированной и не влияет на постановку и ход решения задачи.

Радиус-вектор — Вектор, определяющий положение М. Т. в пространстве:  . Здесь   — координаты радиус-вектора. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора (или его координат  ) от времени   называется законом движения.

Траектория — Годограф радиус-вектора, то есть — воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется М. Т. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или вульгарно — путем и обозначают буквой S. При таком описании движения S выступает в качествеобобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:

,

Где :   — модуль начальной скорости, а   — Тангенциальное ускорение.

Описание движения при помощи понятия траектории — один из ключевых моментов классической механики . В квантовой механике движения носит бестраекторный характер, а само понятие траектории теряет смысл.

Пемемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:

.

Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.

Средняя скорость — векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:

.

Мгновенная скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени:

.

Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:

.

Единица измерения скорости в системе СИ— м/с, в системе СГС — см/с. Мгновенная скорость всегда направлена по касательной к траектории.

Мгновенное ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:

.

Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения:

.

Здесь   — единичный вектор нормали,   — единичный вектор касательной. Величина   называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории:

.

В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.

Величина   называется тангенциальным ускорением и характеризует величину изменения модуля скорости:

.

Динамика

Динамика — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, момент импульса, энергия^[1].

Также динамикой нередко называют, применительно к другим областям физики (например, к теории поля), ту часть рассматриваемой теории, которая более или менее прямо аналогична динамике в механике, противопоставляясь обычно кинематике (к кинематике в таких теориях обычно относят, например, соотношения, получающиеся из преобразований величин при смене системы отсчета).

Иногда слово динамика применяется в физике и не в описанном смысле, а в более общелитературном: для обозначения просто процессов, развивающихся во времени, зависимости от времени каких-то величин, не обязательно имея в виду конкретный механизм или причину этой зависимости.

Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду.

Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.

С помощью законов динамики изучается также движение сплошной среды, т. е. упруго и пластически деформируемых тел, жидкостей и газов.

В результате применения методов динамики к изучению движения конкретных объектов возник ряд специальных дисциплин: небесная механика, баллистика, динамика корабля, самолёта и т. п.

Основная задача динамики

Исторически деление на прямую и обратную задачу динамики сложилось следующим образом.

• Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.

• Обратная задача динамики: по заданным силам определить характер движения тела.

Законы Ньютона

Инерциальная система отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике: «Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным». Законы Ньютона, а также все остальные аксиомы динамики в классической механике формулируются по отношению к инерциальным системам отсчёта.

Классическая динамика основана на трёх основных законах Ньютона:

• 1-й: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано.

• 2-й: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

где   — ускорение тела,   — силы, приложенные к материальной точке, а   — её масса, или

В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами^[2][3].

Второй закона Ньютона можно также сформулировать с использованием понятия импульса:

В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на него силе^[4].

где   — импульс (количество движения) точки,   — её скорость, а   — время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени^[5][6][7].

• 3-й: Тела действуют друг на друга силами равными по модулю и противоположными по направлению

Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса

Законы Ньютона в неинерциальных системах отсчета

Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:

,

где   — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчета.

Формулы некоторых сил, действующих на тело

• Сила всемирного тяготения:

или в векторной форме:

вблизи земной поверхности:

• Сила трения:

• Сила Архимеда:

Закон сохранения импульса

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Как и любой из фундаментальных законов сохранения, закон сохранения импульса связан, согласно теореме Нётер, с одной из фундаментальных симметрий, — однородность пространства.

Вывод в механике Ньютона

Согласно второму закону Ньютона для системы из N частиц:

где   импульс системы

а   — равнодействующая всех сил, действующих на частицы системы

Здесь   — равнодействующая сил, действующим на n-ю частицу со стороны m-ой, а   — равнодействующая всех внешних сил, действующих k-ю частицу. Согласно третьему закону Ньютона, силы вида   и   будут равны по абсолютному значению и противоположны по направлению, то есть  . Поэтому вторая сумма в правой части выражения (1) будет равна нулю, и получаем, что производная импульса системы по времени равна векторной сумме всех внешних сил, действующих на систему:

Внутренние силы исключаются третьим законом Ньютона.

Для систем из N частиц, в которых сумма всех внешних сил равна нулю

или для систем, на частицы которых не действуют внешние силы   (для всех k от 1 до n), имеем

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:

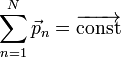 (постоянный вектор).

То есть суммарный импульс системы из N частиц, где N любое целое число, есть величина постоянная. Для N=1 получаем выражение для одной частицы.

Если векторная сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, то есть не меняется со временем.

Закон сохранения импульса выполняется не только для систем, на которые не действуют внешние силы, но и для систем, сумма всех внешних сил равна нулю. Равенство нулю всех внешних сил достаточно, но не необходимо для выполнения закона сохранения импульса.

Если проекция суммы внешних сил на какую-либо направление или координатную ось равна нулю, то в этом случае говорят о законе сохранения проекции импульса на данное направление или координатную ось.

Закон сохранения механической энергии.

В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть в никуда.

Примеры

Классическим примером этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно^]. В случае математического маятника аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.

Вывод из уравнений Ньютона

Закон сохранения механической энергии может быть выведен из второго закона Ньютона, если учесть, что в консервативной системе все силы, действующие на тело, потенциальны и, следовательно, могут быть представлены в виде

,

где   — потенциальная энергия материальной точки (  — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид

,

где   — масса частицы,   — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что  , можно получить

Путём элементарных операций это выражение может быть приведено к следующему виду

Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.

Этот вывод может быть легко обобщён на систему материальных точек.

Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Простым языком, кинетическая энергия - это энергия, которую тело имеет только при движении. Когда тело не движется, кинетическая энергия равна нулю.

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

 — есть равнодействующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы  . Учитывая, что  , получим:

Если система замкнута, то есть внешние по отношению к системе силы отсутствуют, или равнодействующая всех сил равна нулю, то  , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

 — масса тела

 — скорость центра масс тела

 — момент инерции тела

 — угловая скорость тела.

Физический смысл работы

Работа всех сил, действующих на частицу при её перемещении, идёт на приращение кинетической энергии частицы:

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы.